等温の極意〜冬本番を前に〜

こんにちは、ヒラタです。寒くなってきたので等温系の話をします。

等温系とは

我々の住む世界は大体等温です。つまり熱的な平衡状態にあります。これは周囲の環境が熱浴と接触しているためです。

カノニカルモデル

熱浴の温度が変化しない限り、世界は等温であり続けます。他にも平衡状態を作る方法はいくつかありますが、今回はこの等温モデルについてまとめようと思います。

断熱モデルの詳しい話はコチラ↑

状態の実現しやすさ

断熱系ではエントロピーの大きい状態であるほど実現しやすいです。これはどうしてだったかを思い出してみましょう。

Sは状態数Wの単調増加関数

では、等温系ではどうでしょうか。実は等温系の場合は異なる状態a,bの実現確率は必ずしも一致しません。等重率の原理が成り立たないわけです。

※例えば、気体分子はある程度低温だと移動速度が遅まって、エネルギー的に安定化します。つまり、低温系ではエネルギーが低い状態の実現確率はそれ以外の状態のものと比べて大きくなります。

結論から言うと、各状態はexp(-βE)に比例する確率で実現します。βは逆温度、Eは状態のエネルギーです。数式だと以下のようになります。

分母は規格化定数で、式の中のexp(-βE)はボルツマン因子と呼ばれます。

ボルツマン因子の導出自体は後々やるとして、とりあえずこいつの性質を調べてみましょう。

ボルツマン因子を足しまくる

各状態のボルツマン因子を脳死で合計してみます。

状態のラベルiについてのΣをエネルギーE_iについてのΣに書き換えました。その過程で、同一の準位E_iに属する状態数W(E_i)が参入しますが、こいつはエントロピーS*(E_i)を用いて表せます。

結局、以下の式に落ち着きます。

この数列和のうち、答えに寄与する項はexpの中身が最大の部分、つまり「E-TS*(E)が最小となるE」の近傍だけです。

そのようなEの値をE_0とおきます。実際、exp{-β(E-TS*(E))}のグラフは下図のようになり、E_0から離れたEが和に寄与しないことが分かります。

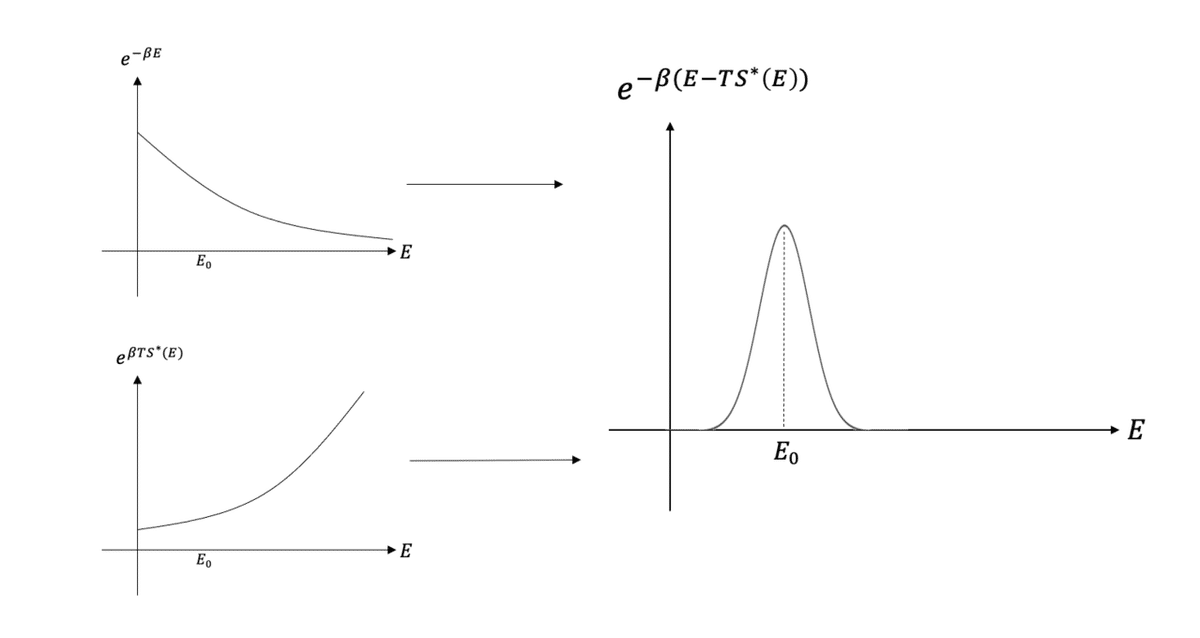
指数関数×W(E)→ガウス分布

E-TS*(E)のことをF(T,E)とおきましょう。F(T,E)はE=E_0で最小値F*(T)をとります。この関数F*(T)を自由エネルギーと呼びます。

等温系では、Fが小さい状態ほど実現確率が高くなります。つまり、最も実現しやすいエネルギー値はE_0です。

F*(T)はE(S*)のルジャンドル変換

※ルジャンドル変換では、入力する関数によって情報を損なう可能性があります。E(S*)⇔F*(T)が1対1で漏れなく対応することはE(S*)が下凸関数であること（熱力学第二法則）と深く関係しています。

自由エネルギーはなんでも知ってるね

各状態のボルツマン因子の合計から関数F*(T)が求まります。
そして、この関数F*(T)は等温モデルの全ての情報を持っています。これは関数E(S*)が断熱モデルの全情報を持つことと似てます。

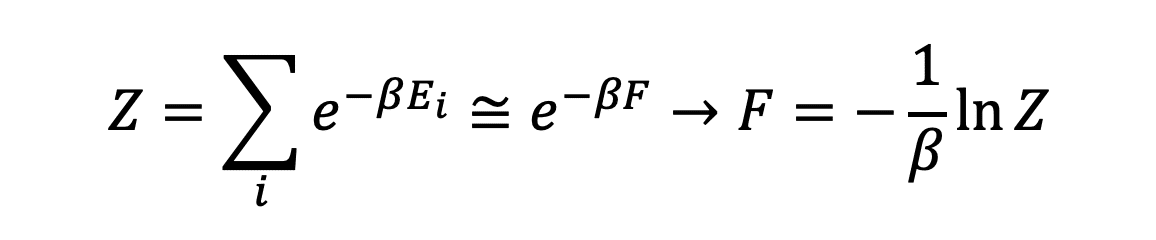
F[T;V,N]の全微分を考えると、他の熱力学量の求め方が見えます。

求めたFとSの値から、対応するEの値E_0を求めてみましょう。

E_0はエネルギーの期待値なので、この式から「状態iの実現確率がボルツマン因子で表せる」ことが導けたことになります。

断熱モデルとの関係

最後に、断熱と等温の２つのモデルから導かれる結果を比べてみましょう。それぞれのモデルについて、状態実現確率は下図のようになります。

断熱モデル（左）、等温モデル（右）

２つのグラフは別物のようですが、系の自由度が十分大きければ一致します。

断熱モデル（左）、等温モデル（右）

大抵の場合、モデル内の粒子数は10^23くらい大きいので、断熱モデルと等温モデルは等価なものとして問題ありません。

※等価ではあっても、後者の方が圧倒的に汎用性が高いです。断熱の場合、系のとりうるEごとにSの値を調べなければ何も出来ませんが、等温モデルでは系のとりうるEの値さえ分かれば他のどんな情報も求められます。

おわりに

長くなりましたが、以上が等温系に関するまとめになります。

ボルツマン因子は大学物理・化学でよく目にしますが、あまり深く考えずに使いがちです。時々、数式の背景にも思いを馳せてみると全体の理解がより深まるかもしれません。

2021年も残すところあと僅かとなりました。年末に風邪など引かぬよう、部屋は等温系にして過ごしましょう。

それでは、よいお年を。