完全均衡点～ゲーム理論３～

前回までの復習

前回までの記事

では戦略形ゲームと展開形ゲームの数理モデルの均衡点について学んだ。戦略形ゲームとは１回の表出で(混合)戦略を表出するゲームであり、展開形ゲームは将棋のように複数の時間軸的手番が存在するゲームの木として表現可能なゲームになる。戦略形ゲームは最もシンプルなモデリング法であり、実は展開形ゲームは(例えばエージェントと呼ばれる概念を用いる事で)戦略形ゲームと見ることが出来る。故に戦略形ゲームの定理が展開ゲームの言葉にもにも還元でき、均衡点の存在定理等を導くことが出来る。展開形ゲームは数学的に戦略形ゲームと言えど、現実的には手番が存在する事による本質が存在する。展開形完全情報ゲームにおける理論的にもアルゴリズム的にも重要な定理(手法)がbackward inductionと呼ばれるものになる。これを理解するには部分ゲームとその縮約ゲームと呼ばれる概念の理解が必須となる。

ゲーム理論(岡田章)第４章

Amazon.co.jp: ゲーム理論〔第3版〕 : 岡田 章: 本

さて、第４章においてはナッシュ均衡点の概念が見直される。ゲーム理論の均衡概念の目的は合理的行動の理解である。一方ナッシュ均衡点の定義は、各プレイヤーが均衡プレイにおいて利得における最適反応を示している事、即ちこの意味で均衡プレイ時に行動変更のインセンティブを持たない事である。つまり均衡プレイに陥るとそこから動くことは無いという意味(※例えば曲線にそってボールを転がし極値的窪みにハマるような状況)で合理的行動ならば満たされるべき必要条件となっていると見れる。しかし、均衡点であるからと言ってその全てが有効とみれる訳ではなく、状況によっては解に対して更に望ましい性質を付けるべき場合が存在する。第４章においては均衡点の精緻化を目的として記事で紹介する解の概念を新たに定義する。(※以下では均衡点のタイプを歴史的な登場順や解説をすべき順ではなく強い順に並べた。)

例：チェーンストアゲーム

図：チェーンストアゲーム

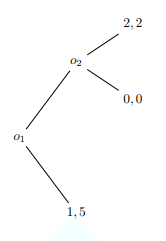
プレイヤー１を実業家(Up, Down)、プレイヤー２をチェーンストア(Up, Down)とする。ある街においてチェーンストアが独占販売している時、実業家がその場所で新たに起業した時にチェーンストアは協力(U)するか、協力しないか(D)のゲームモデルである。この時実業家は参入(U)、撤退(D)を選ぶものとする。例として実業家が参入(U)し、チェーンストアが協力(U)した場合に両者の利得は２となる。ここでナッシュ均衡は参入、協力タイプの$${e_1 = (U, U)}$$と、撤退、非協力タイプの$${e_2 = (D, D)}$$の２つとなる。しかし、タイプ$${e_2}$$の均衡点はチェーンストアが信ぴょう性のない脅しと呼ばれる概念を使った偽の均衡点であり、合理的な実業家は均衡点$${e_2}$$にはならないと見抜いてしまう。その解説は下記で行おう。

完全均衡点

今回紹介する概念の中で最も強いものであり解の安定性を与える概念である。
さて、チェーンストアゲームの$${e_2}$$は何故信ぴょう性のない脅しと呼ばれるのであろうか？ひとつそれは解の不安定さによる。即ちチェーンストアの協力しない($${D}$$)という態度は仮に実業家が本当に参入$${U}$$してきたら手のひらを返し、協力$${U}$$という態度を取る。人間というのはその不完全性によって１００％合理的な判断を出来る訳では無いし、またゲームモデルとしての完全な理解も現実的には難しいだろう。という訳でチェーンストアがいくら非協力的態度を取ったとしても実業家は参入してしまう可能性もあるだろう。この時にチェーンストアの戦略は非協力$${D}$$から協力$${U}$$という真逆の反応を示してしまう事になる。つまり実際にプレイするつもりのない非協力$${D}$$はチェーンストアにとって脅しに過ぎないのであって均衡点で在りさえすれ本来的に望ましくない均衡点なのである。解の安定性を与えるには各々の枝$${c \in A(u)}$$に対して心的に制御不能な戦略の揺れ$${\eta_c > 0}$$に対して整合的な均衡点になっていないといけない。即ち合理性の破綻とはプレイヤー$${1 \leq i \leq n}$$の戦略変数$${\hat{p}_c}$$について$${\hat{p}_c \geq \eta_c}$$という制約条件を加える事と同じである。この制約を加えたゲームを変動ゲーム$${\hat{\Gamma} = (\Gamma, \eta)}$$という。ここで完全均衡点とは均衡点$${b^\ast}$$が変動ゲームの列$${\hat{\Gamma}^k = (\Gamma, \eta^k)}$$の均衡点$${\hat{b}^k}$$で近似できる事であり、即ち

1. 任意の枝$${c}$$に対して$${\eta^k_c \rightarrow 0}$$

2. 変動ゲームの均衡点$${\hat{b}^k}$$が存在し$${\hat{b}^k \rightarrow b^\ast}$$

となる事である。こうすると完全均衡点においてはチェーンストアは実業家が参入という選択肢を取るという可能性がある限り、その変動ゲームの最適反応として非協力的態度を取ることは出来ない故、その極限的均衡点である完全均衡点においても非協力的態度が取り除かれ、解の安定性の観点から脅しというプレイが取り除かれることになる。

逐次均衡点

完全均衡点は変動ゲームの列の極限として元ゲームを捉える事にあるが、重要な事は変動ゲームは全ての枝に対してその行動戦略に対して正の確率を付与しているという事であり、これを行動戦略の組$${b}$$は完全に確率的であるという。これに対し逐次均衡点とは均衡戦略の変動を各プレイヤーの予想形成のみに用いるものである。行動戦略の組$${\hat{b}}$$と手番$${x}$$と情報集合$${u}$$に対して条件付確率$${p(x|\hat{b})}$$と$${p(u|\hat{b})}$$をそれぞれ定義できる(※それぞれ行動戦略の組$${\hat{b}}$$の元、手番or情報集合に到達する条件付確率と思う)。完全確率的な変動ゲームの行動戦略の組においては分母が非０の為Bayes' ruleによって条件付確率$${p_u(x|\hat{b}) = \frac{p(x|\hat{b})}{p(u|\hat{b})}}$$が定義できるだろう。このベイジアン意思決定論の立場から、もし行動戦略の組$${b}$$が完全確率的であるのならば情報集合における信念$${\rho_u(x|b)}$$(※言わば各情報集合における予想形成)を再びBayes' ruleから定義できるだろう。これを行動戦略から導かれる信念と呼ぶ。逐次均衡点$${(b^\ast, \rho^\ast)}$$とは、最適反応の組である均衡点がこうした信念の列$${\rho_k}$$と整合的な信念を持つ事を期待する概念である(※詳細略)。(意味的に)明らかに完全均衡点は逐次均衡点なのであるが、逆は言えない(※詳しくは成書における詳細な数理的定義と定理をご覧ください)。

部分ゲーム完全均衡点

行動戦略の組$${b^\ast}$$が$${\Gamma}$$の全ての部分ゲームに対してナッシュ均衡点を導く事であり、紹介する中では最も弱い(※ナッシュ均衡よりは強い)均衡点の概念である。明らかにチェーンストアゲームの部分ゲーム完全均衡点は$${e_1}$$のみであり、信ぴょう性のない脅しを排除することが出来る。またこれは前に紹介したbackward inductionに同じである。

まとめ

均衡点の精緻化について基本的な事を紹介した。本には他にも興味深い均衡点のタイプとその応用が書いてある。記事では応用的観点を割と飛ばしている所があるのでそこを追ってみるのも良いかもしれない。また今回紹介したチェーンストアゲームの拡張的なゲームにおいて、チェーンストアパラドックスと呼ばれる均衡点の問題(※それは完全均衡点の問題でもある)があるのだが、それは未だに十分な説明がなされていないとの事であり未解決の問題である。本では素人でも割と簡単にopenな問題を知れて面白いと思う。

スキ、フォロー、シェアよろしくお願いいたします！！！