
時系列データをpython【#2.3】自己相関
以下の本から時系列データの部分を勉強しましたので、少しここに書こうと思います。※アフェリエイトはしていません。でもこの本はすごくいい本なので、これで知識を増やす、勉強するのはいいことだと思います。(アフェリエイトではなく、自分の一生ものの能力をつけるために約3000円でこの本を買って、月給3000円上げようというモチベーションです。)
前回「ARモデル(Autoregressive model)」を理解できずに頓挫していました。そのあと、理解が深まる本を探し↑の本にたどり着きました。第9章に自己相関係数に関して載っていたので、それを見て学びました。
以下のキーワードを理解してから、進めていきます。
1.分散
2.共分散
3.相関係数
4.自己相関のラグ
1.分散
面倒なのでwikipediaからとってきました。

たとえば、5人のクラスの国語の点数が10,30,50,70,90点だった場合、平均は50点です。その50点がxbarです(私に教えてくださった先生の分野ではμです)。n=5(5人のため)で、式は、1/5 * ((10 - 50) ^2 + (30 - 50) ^2 +…)と続きます。なので、(10 - 50)のように平均からの差を出しているので、差=ばらつきを出しています。±あるので、-10と10をそのまま足すのゼロになります。そうならないように2乗しています。そうすると-10^2=100、10^2=100になって、足してもゼロにはなりません。そのあと、全部足し終わったら5人で割って、一人当たりの差=ばらつきを出しています。ここで、左辺がs^2になっているのは2乗しているからです。(1/nは1/(n-1)のときもあります、割愛します)
2.共分散
これもwikipediaからとってきました。

分散を記載した人と全然違う書き方をしていますね。専門分野が違うんですかね。私は昔は、、、σ_x,yとかだったかなぁ。。。
Covは関数の意味ですかね。Eはexpectationなので期待値、平均をするってことですね。
こっちの人の書き方のほうが私には合うのでこっちで書き直します。

これだと、yがxに変われば、普通の分散と同じということがわかりますかね。なので、xとyのばらつきをみているということですね。(xi_xbar)が正で、(yi_ybar)が正ならば掛け算の結果は正、(xi_xbar)が負で、(yi_ybar)が負ならば掛け算の結果は正。(xi_xbar)と(yi_ybar)の符号が正負ばらばらならばマイナスになります。なので、正と正、負と負の場合は数値が大きくなって、正負ばらばらだと数値は小さくなっていく。私と同僚の毎月の給料が一緒に変動していると共分散(≒相関)は高くなって、私と前職の知人の給料が同じ変動をしていなければ共分散(≒相関)は低くなります。
相関との違いは、給料の例で言うと、毎月約10万円の給料のxiと100万円の給料のyiのように桁違いのものを扱うとき、数字を見ただけでパッと共分散が高いのか低いのかわからないことです。相関にすれば、-1から1の間に数値が収まるので、どんなものを扱っていても、相関という数値で比較が可能になります。(説明長い、、、)
ちなみに、数式には、イタリック(斜体)したり、しなかったりとか書き方のマナーがあります。うろ覚えですが、↓のが参考になるかと思います。
3.相関係数(ピアソンの積率相関係数)
ちょうど、スピアマンの順位相関係数とかを勉強しているところだったので、あえてピアソンの積率相関係数という言葉も併記しました。
これは共分散のときと同じホームページを参考にします。
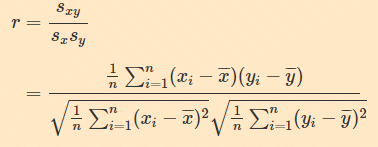
分子を共分散、分母をsqrt(xの分散)とsqrt(yの分散)の掛け算にしたものです。yとxの桁が違っても、この分母で正規化(-1から1にスケーリング)してくれます。
4.自己相関のラグ
やっと本題にいきます。この相関のxは時系列データ、yはそのxをなんこかずらしたものです。このずらすことをラグといいlag=1とか、2とかずらして相関をみます。前回、ChatGPTがlag=2を「過去2期ずらす」的なことを言って「期って何?」って思っていましたが、単純に-2したものです。
んで、ここで無駄にChatGPT3.5にわかりやすい表を書いてもらいました。


表の左側がxで、表の右側がy(xのlag=1)だと思っていただければいいと思います。これだと、一番最後のところに空欄ができるので、ラグがないときに比べて(7日分)、計算する個数は1つ減ります(6日分)。ラグを変化させていっても分母の分散はいつも一定です。
あれ?ARモデルの話にたどり着かない…
#python
#ChatGPT
#プログラミング初心者
#生成AI
#プログラミング教育
#GoogleColab
#時系列
この記事が気に入ったらサポートをしてみませんか?
