
「情報関係基礎」過去問を教材化する:2012 年:上皿天秤
2012年度の問題は,上皿天秤を使って物体の重さを量る問題。
前半は2進法,後半は3進法の問題だが,3進法の問題が難しい。ガイドに従えば答えられるのだが,本当に意味がわかって答えられるかというと怪しい。そういう意味では,「わかっていなくて答えられる」ということになりかねない設問ともいえる。生徒は基数変換が意外にわかっていないからだ。
まずは,オリジナル準拠(マーク式のもとの問題と同じにはなっていない)のものを示そう。そこで,何が問題点かを示し,説明を詳しくした案を示す。
======================================
その1 オリジナル準拠
質量 x グラムの物体と,与えられた分銅を用いて,上皿天秤をつり合わせる。そのために適切な分銅の載せ方を重い順に表示するプログラムを考える。x は 1 以上1000以下の整数とする。
問1 次の条件で,上皿天秤を釣り合わせることを考える。
<使用法> 物体は左の皿だけに載せ,分銅は右の皿だけに載せる。
<分 銅> 表1に示す質量の分銅がそれぞれ 1 個ずつある。
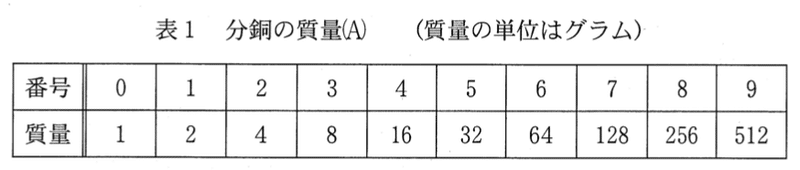
x = 713 の場合 713 = 512 + 128 + 64 + 8 + 1 から,9番,7番,6番,3番,0番の分銅を右の皿に載せればよい。
表 1 における n 番の分銅は 2のn乗 グラムなので,x を2で繰り返し割って余りを求めていけば,載せる分銅がわかる。x = 713 の場合の例を次に示す。

たとえば (g) は表1の6 番の分銅に対応する計算である。
この考え方に基づいて,次のプログラムを作った。x の値は 変数 x に格納されている。結果を記録するリスト Kekka1 は要素数10で,添え字は0から始まる。また,2つの整数 a≧0 , b>0 に対し,a を b で割るとき,a // b は商の整数部分を, a % b は余りをそれぞれ計算する。
ア,イ,ウ,エ,オ,カ に適するものを選択肢から選んで書いて完成しなさい。
Kekka1 = list(range(10))
for i in range(10):
Kekka1[i] = 0
x = 713
i = 0
while x > 0:
Kekka1[ア] = イ
ウ = エ
i = i + 1
for j in range(9, -1, -1):
if Kekka1[オ] == カ:
print(オ, end="番, ")
print("の分銅を右の皿に載せる。")<選択肢>
(1) 0 (1) 1 (2) 2 (3) 3 (4) x + 2 (5) x * 2 (6) x // 2 (7) x % 2
(8) i (9) j (a) x (b) Kekka1[i] (c) Kekka1[j] (d) Kekka1[x]
問2 今度は,次の条件で上皿天秤を釣り合わせることを考える。
<使用法> 物体は左の皿だけに載せるが,分銅はどちらの皿に載せてもよい。
<分 銅> 表2に示す質量の分銅がそれぞれ 1 個ずつある。
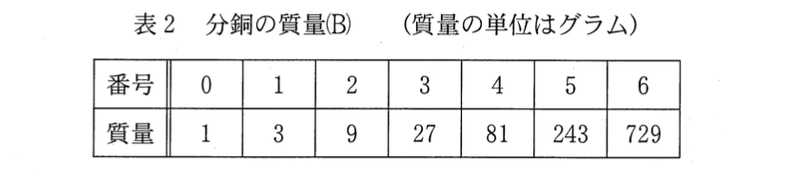
表2における n 番の分銅は 3 の n 乗グラムなので,割る数を2から3に変えて,問1 の考え方を用いる。すると,割り算の余りが2となり,分銅が2個必要になる場合がある。しかし,分銅はそれぞれ1 個ずつしかない。この場合
![]()
から,左の皿に n 番の分銅を載せ,物体の質量がその分増えたものと考え,n+1 番の分銅を載せるか否かの判断に進む。たとえば,x = 18 の場合,左の皿に(キ)番の分銅を,右の皿に(ク)番の分銅を載せればよい。キ,クに適する数を答えなさい。[注1]
この考え方を元にすると,x = 97 の場合,
97 = 81 + 27 - 9 - 3 + 1
から,4番,3番,0番の分銅を右の皿に,2番,1番の分銅を左の皿に載せればよい。
x = 97 の場合を例として,左の皿に分銅を載せたとき,その分だけ物体の質量が増えたものと見なす処理を考えよう。
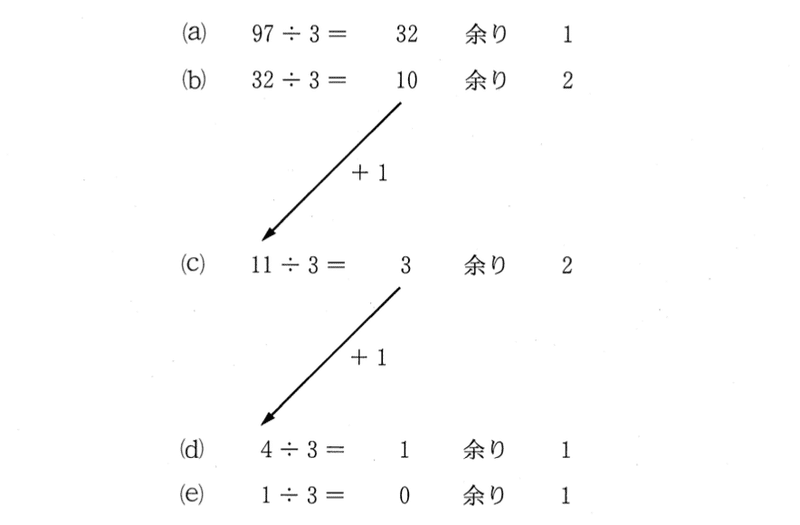
上の(b)で,余りが2となるので,左の皿に1番の分銅(3グラム)を載せる。そのとき,その分だけ物体の質量が増えたものと見なす。そのためには,(b) の商10 に1を加えた11 を,(c) において割られる数とすればよい。[注2]
上の(c) でも余りが2となるので,同様に考える。
上の考えをもとにして,プログラムを作った。x の値は,変数 x に格納されている。結果を記録するリスト Kekka2 は,要素数7で,添え字は0から始まる。また,リスト Sara は,「右」または「左」の文字を表示するために用いる。割り算の余りはいったん 変数 amari に代入する。ケ〜チに適するものを書いて完成しなさい。[注3]
Sara = ["", "右", "左"]
Kekka2 = list(range(7))
for i in range(7):
Kekka2[i] = 0
x = 97
i = 0
while x > 0:
ケ = x % 3
コ = x // 3
Kekka2[サ] = シ
if ス == セ:
x = ソ
i = i + 1
for j in range(6, -1, -1):
if Kekka2[タ] != チ:
print(タ, "番の分銅を", Sara[チ], "の皿に載せる。")もとの問題ではこのあと選択肢があるが,ここでは省略。その分難しくなるが,意味がわかれば書けるはずだ。
===================================
文中,[注]と書いた箇所について説明する。
[注1]
![]()
から,左の皿に n 番の分銅を載せ,物体の質量がその分増えたものと考え,n+1 番の分銅を載せるか否かの判断に進む。たとえば,x = 18 の場合,左の皿に(キ)番の分銅を,右の皿に(ク)番の分銅を載せればよい。
x = 18 のとき,上の式をまねすると x = 9×2 = 9( 3 -1 ) = 27 - 9 となって計算が合う。それで「上の式」の意味がわかっていなくてもなんとなく キ,ク は答えられるのである。しかし,なぜ「上の式」から,「物体の質量がその分増えたものと考え」るのだろう。
それを理解するには,x = 18 の場合について,もう少しきちんと考えていかなければならない。
18 を 3進法の各位の累乗を使った形で表すと
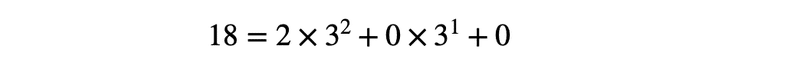
と書ける。このとき,18 = 9×2 = 9( 3 -1 ) = 27 - 9 であることを利用して
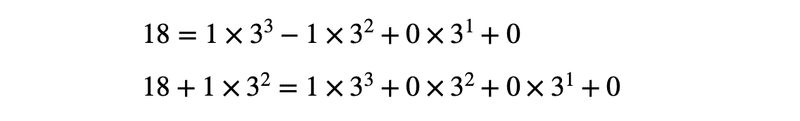
と変形できる。したがって,左の皿(左辺)に2番の分銅を置いて,右は3番の分銅を置けば釣り合うわけだ。
[注2]
では,余りを求めていく手続きで,余りが2なら,商に1を加えるのはどういうとことだろう。
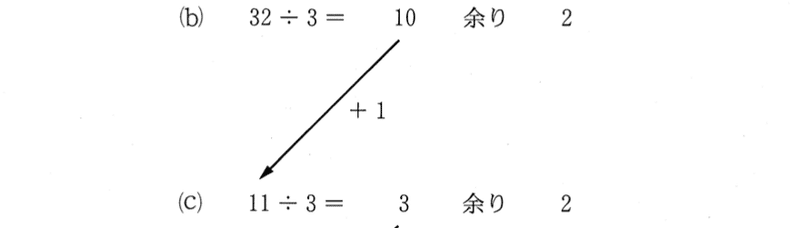
32を次のように変形してみよう。
32 = 10×3 + 2
32 = 10×3+(3-1)
32 = 11×3 -1
32 + 1 = 11×3
となって,左の皿に分銅をひとつ置くことになる。右の皿は11から計算を進めるわけだ。
このとき,「この段階で余りが2」であることを記憶しておけば,それを使って最後に式を表現できる。それが[注3]だ。
[注3]
リスト Kekka2 には,余りが 0, 1, 2 のいずれかが記録されている。これを見て
0 なら分銅は載せない
1 なら右に載せる
2 なら左に載せる
という判断をしていけばよい。Sara = ["","右","左"] なので,1,2 と右・左が対応する。したがって,「1か2か」の判断は不要で,
print(タ, "番の分銅を", Sara[チ], "の皿に載せる。")
の1行で表示ができるのである。
次の改訂案では,「余りが2なら,商に1を加える」理由がわかりやすいように説明を書いていく。また,10進法から2進法への換算の方法:次々に2で割る:は知っているものとする。
その2 改訂案
質量 x グラムの物体と,与えられた分銅を用いて,上皿天秤をつり合わせる。そのために適切な分銅の載せ方を重い順に表示するプログラムを考える。x は 1 以上1000以下の整数とする。
問1 次の条件で,上皿天秤を釣り合わせることを考える。
<使用法> 物体は左の皿だけに載せ,分銅は右の皿だけに載せる。
<分 銅> 表1に示す質量の分銅がそれぞれ 1 個ずつある。

x = 713 の場合 713 = 512 + 128 + 64 + 8 + 1 から,9番,7番,6番,3番,0番の分銅を右の皿に載せればよい。
これは,713を2進法で表したときの各位の数になっている。
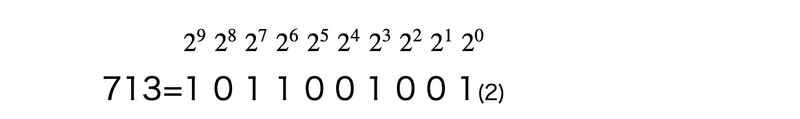
したがって,x を2で繰り返し割って余りを求めていけば,載せる分銅がわかる。x = 713 の場合の例を次に示す。

この考え方に基づいて,次のプログラムを作った。x の値は 変数 x に格納されている。結果を記録するリスト Kekka1 は要素数10で,添え字は0から始まる。また,2つの整数 a≧0 , b>0 に対し,a を b で割るとき,a // b は商の整数部分を, a % b は余りをそれぞれ計算する。
ア,イ,ウ,エ,オ,カ に適するものを選択肢から選んで書いて完成しなさい。
Kekka1 = list(range(10))
for i in range(10):
Kekka1[i] = 0
x = 713
i = 0
while x > 0:
Kekka1[ア] = イ
ウ = エ
i = i + 1
for j in range(9, -1, -1):
if Kekka1[オ] == カ:
print(オ, end="番, ")
print("の分銅を右の皿に載せる。")<選択肢>
(1) 0 (1) 1 (2) 2 (3) 3 (4) x + 2 (5) x * 2 (6) x // 2 (7) x % 2
(8) i (9) j (a) x (b) Kekka1[i] (c) Kekka1[j] (d) Kekka1[x]
問2 今度は,次の条件で上皿天秤を釣り合わせることを考える。
<使用法> 物体は左の皿だけに載せるが,分銅はどちらの皿に載せてもよい。
<分 銅> 表2に示す質量の分銅がそれぞれ 1 個ずつある。

たとえば,x = 18 の場合,
18 = 9 × 2
であるが,質量9の分銅は1つしかない。そこで,
18 = 9 × ( 3 - 1 )
18 = 27 - 9
18 + 9 = 27
と変形する。 すなわち,左の皿に(キ)番の分銅を,右の皿に(ク)番の分銅を載せれば左右が釣り合うことになる。キ,クに適する数を入れなさい。
次に,x = 97 の場合を考えてみよう。問1のように,次々に3で割って余りを求めていく手順を考える。
97 ÷ 3 = 32 余り 1 ・・・・ 1gの分銅を右に載せる
32 ÷ 3 = 10 余り 2 ・・・・ 32 = 3×10+2 なので
32 = 3×10 +(3-1)
32 = 3×11 - 1 と変形
そこで,商の10 に1を加えて11とし
3gの分銅は左に載せる。
すなわち,余りが2のときはその
分銅は左に載せることになる。
11 ÷ 3 = 3 余り 2 上と同様に処理をする。
以下,同様に続ける
上の考えをもとにして,プログラムを作った。x の値は,変数 x に格納されている。結果を記録するリスト Kekka2 は,要素数7で,添え字は0から始まる。また,リスト Sara は,「右」または「左」の文字を表示するために用いる。割り算の余りはいったん 変数 amari に代入する。ケ〜チに適するものを書いて完成しなさい。
Sara = ["", "右", "左"]
Kekka2 = list(range(7))
for i in range(7):
Kekka2[i] = 0
x = 97
i = 0
while x > 0:
ケ = x % 3
コ = x // 3
Kekka2[サ] = シ
if ス == セ:
x = ソ
i = i + 1
for j in range(6, -1, -1):
if Kekka2[タ] != チ:
print(タ, "番の分銅を", Sara[チ], "の皿に載せる。")