Cinderellaでカオスを描く:ローレンツアトラクタ
ローレンツアトラクタはカオスの中で最もポピュラーなものでしょう。蝶の羽のような図はWeb上にもたくさんあります。Excelを用いたもの、POV-Rayを用いたもの、JAVAを用いたものなど、アトラクタを描くためのソフトウェアもさまざま。Mathematicaにはローレンツアトラクタを描く例があります。
コードは
s = NDSolve[{Derivative[1][x][t] == -3 (x[t] - y[t]), Derivative[1][y][t] == -x[t] z[t] + 26.5 x[t] - y[t], Derivative[1][z][t] == x[t] y[t] - z[t], x[0] == z[0] == 0, y[0] == 1}, {x, y, z}, {t, 0, 400}, MaxSteps -> \[Infinity]];
Show[ParametricPlot3D[Evaluate[{x[t], y[t], z[t]} /. s], {t, 0, 400},
PlotPoints -> 1000, PlotStyle -> Directive[Thick, RGBColor[.8, 0, 0]], ColorFunction -> (ColorData["SolarColors", #4] &)], Graphics3D[{ColorData["SolarColors"][0],
Sphere[First[({x[t], y[t], z[t]} /. s) /. t -> 0], .75]}], RotationAction -> "Clip", Boxed -> False, SphericalRegion -> False, Axes -> False, ImageSize -> 500]
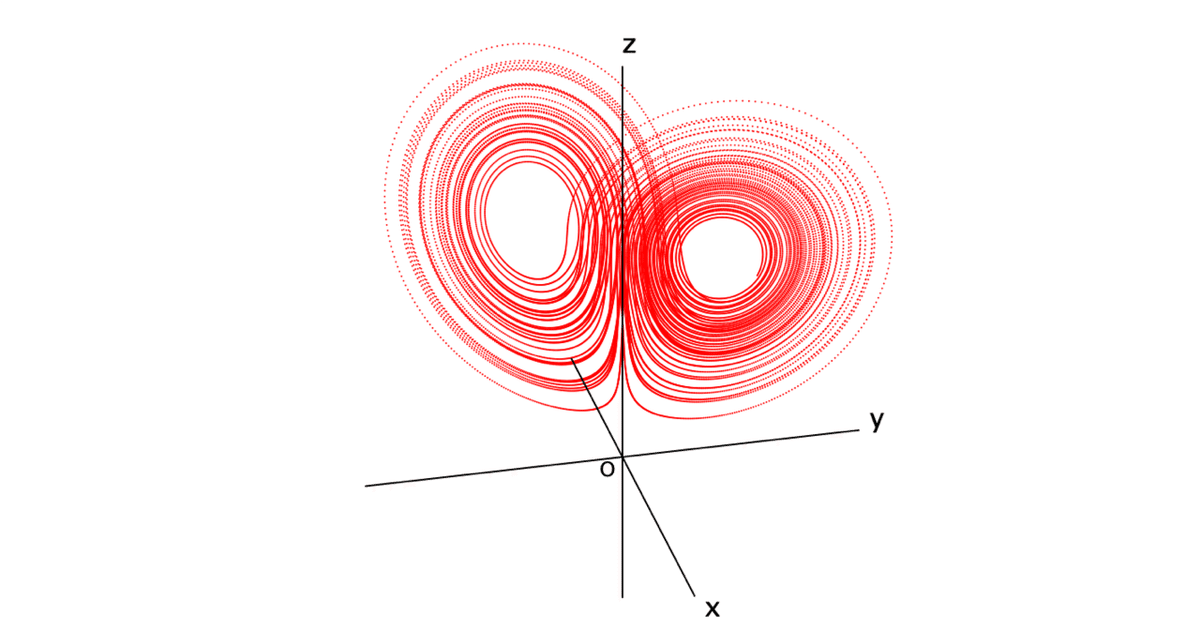
次の図ができます。

NDSolve が微分方程式を解く関数です。CindyScriptには微分方程式を解く関数はないので,常微分方程式であるローレンツの式を、数値的に解いていくことにします。
ローレンツの式
ローレンツアトラクタとは、気象学者のローレンツが大気変動モデルを研究していて導き出した微分方程式の解が描く図形です。
ローレンツの式は次の連立常微分方程式です。
$${\dfrac{dx}{dt}=-\sigma(x-y)}$$
$${\dfrac{dy}{dt}=-xz+rx-y}$$
$${\dfrac{dz}{dt}=xy-bz}$$
ここで、$${x}$$は対流運動の速度、$${y, z}$$は水平方向と垂直方向の温度変位、係数σはプラントル数、r はレイリー数というもので、b は系の物理的サイズに関わる数です。したがって、空間座標の$${(x,y,z)}$$ ではないのですが、これを空間座標と見なして図を描くのです。このようなものを「相空間」といいます。
微分方程式を解くときは、初期値が必要になりますが、その初期値がわずかに変わっただけで結果が大きく変動し、まさに予測がつかないというわけです。地球の反対側のチリの海岸で誰かがたき火をすると小さな上昇気流が生まれ、日本の台風の進路に影響する、そんなたとえ話ができます。バタフライエフェクトという言葉もあります。
ローレンツは著書「ローレンツ・カオスのエッセンス」(杉山勝・智子訳・共立出版)の中で次のように述べています。
システムのふるまいは、3つの定数 b,r そして σ により決まる。この方程式は精力的に研究されてきており,ケンプリッジ大学のコリン・スパロウは、この方程式だけを扱った1冊の本を書いたほどである。今までしばしばアトラクターと呼んできた構造は,実は,アトラクターに含まれる1つの解の長時間にわたる軌道を描いたものである。たとえば,1章に示されているような蝶を捕まえるために,ますず、b=8/3,σ=10,r=28としてみよう。そして,時間ステップ $${ \Delta t}$$ と$${x,y,z}$$の初期値を適当にとり,数値的に方程式を解くことにする。4次のルンゲ・クッタ法でもよい。何千ステップかコンピュータに計算させた後,ストップさせ,$${z}$$ を縦軸,$${x}$$ を横軸として計算結果をブロットさせれば蝶が得られる。ただし,計算初期の点が過渡的なものならば,それらをブロットせず捨てるものとする。
バタフライは,線で結ばれた一続きの点としてたびたび描かれてきた。だから、それは1本の長い連続曲線のように見える。時間ステップを十分小さくしても同様である。ところが、私がバタフライの新種に初めて出合ったのは,Δt=0.002としようとして、まちがった位置に小数点を打ってしまったときである。
この「まちがった位置に小数点を打ってしまったとき」の図が,本の表紙になっています。

Web 上やYoutubeにはローレンツアトラクタについての記事がたくさんありますが,この「まちがった位置に小数点を打ってしまったとき」の図はほとんどありません。冒頭でMathematicaで描いたような軌道の図がほとんどです。Cinderella でローレンツアトラクタを描くにあたり,この「まちがった位置に小数点を打ってしまった」もやってみましょう。本の表紙のようになりますよ。
さて,「数値的に方程式を解く」は,「微分方程式を解く」に書いた通り,オイラー法とルンゲ・クッタ法があります。まずはオイラー法を使って点をプロットしてみましょう。微分方程式から差分方程式を導きます。
$${x_{n+1}=x_n-s \Delta t(x-y)}$$
$${y_{n+1}=y_n+ \Delta t(-xz+rx-y)}$$
$${z_{n+1}=z_n+s \Delta t(xy-bz)}$$
「Excelで学ぶ理工系シミュレーション入門」(臼田、伊藤、井上共著 CQ出版社)ではExcelを使って4000回計算をした表を作り、散布図として図示しています。しかし、Excelでは3次元の図は描けないので、xyとxzの 2通りを表示しています。CindyScriptなら、3次元の描画も可能なので、3次元で表示しましょう。
3つの差分方程式をそれぞれ、関数として定義します。この中の係数は定数として用意しておきます。ローレンツが特に注目したのは、s=10 , b=8/3 , r=28 です。Δtも小さな値 0.002 を割り当てておきます。
fx(x,y):= x - dt*s*(x - y);
fy(x,y,z):= y + dt*(-x*z + r*x - y);
fz(x,y,z):= z + dt*(x*y - b*z);
s = 10;
b = 8/3;
r = 28;
dt = 0.002;
repeat(10000,
x = 10;
y = 12;
z = 25;
pt = [fx(x,y), fy(x,y,z), fz(x,y,z)];
draw(map3d(pt/10), size -> 0.5, color -> Red, noborder -> true);
);ルンゲ・クッタ法を使うなら次のようにします。
fx(t,x,y,z):=-s*(x-y);
fy(t,x,y,z):=-x*z+r*x-y;
fz(t,x,y,z):=x*y-b*z;
s = 10;
b = 8/3;
r = 28;
dt = 0.002;
x = 10;
y = 12;
z = 25;
t = 0;
repeat(10000,
kx1 = dtfx(t,x,y,z);
ky1 = dtfy(t,x,y,z);
kz1 = dtfz(t,x,y,z);
kx2 = dtfx(t+dt/2,x+kx1/2,y+ky1/2,z+kz1/2);
ky2 = dtfy(t+dt/2,x+kx1/2,y+ky1/2,z+kz1/2);
kz2 = dtfz(t+dt/2,x+kx1/2,y+ky1/2,z+kz1/2);
kx3 = dtfx(t+dt/2,x+kx2/2,y+ky2/2,z+kz2/2);
ky3 = dtfy(t+dt/2,x+kx2/2,y+ky2/2,z+kz2/2);
kz3 = dtfz(t+dt/2,x+kx2/2,y+ky2/2,z+kz2/2);
kx4 = dtfx(t+dt,x+kx3,y+ky3,z+kz3);
ky4 = dtfy(t+dt,x+kx3,y+ky3,z+kz3);
kz4 = dtfz(t+dt,x+kx3,y+ky3,z+kz3);
x = x+(kx1+2kx2+2kx3+kx4)/6;
y = y+(ky1+2ky2+2ky3+ky4)/6;
z = z+(kz1+2kz2+2kz3+kz4)/6;
// 1/10に縮小して表示
draw(map3d([x,y,z]/10), size->0.5, color->[1,0,0], noborder->true);
);両者の図を比べてみましょう。左がオイラー法,右がルンゲ・クッタ法です。
ただし,3次元の図なので,上のコードだけでは描けません。「Cinderellaで3D」のページを参考に,3Dの基本的な設定をしておく必要があります。

視点を動かしてみました。

repeat の回数が,今は10000回ですが,もっと増やすとこれより先の軌道が描かれます。
山口昌男著の「カオスとフラクタル」()には,「平衡点」についての記述があります。
$${-10(x-y)=0}$$
$${-xz+28x-y=0}$$
$${xy-\frac{8}{3}z=0}$$
となる点を「平衡点」といいます。明らかに $${(0,0,0)}$$ がそうですが,それ以外に,$${6\sqrt(2),6\sqrt(2),27}$$ と $${-6\sqrt(2),-6\sqrt(2),27}$$ も平衡点になります。上のプログラムでは $${(10,12,25)}$$ でしたが,これを平衡点に変えると何も描かれません。他の点から出発しても,途中でこの点になればそれ以上先には進まないわけですが,そのような例をつくるのは難しそうです。
では,「まちがった位置に小数点を打ってしまったとき」をやってみましょう。dt = 0.002 を間違えて,dt = 0.02 にすると次のようになりま
す。

視点を回転していくと,ローレンツの本の表紙の図のようになってきます。
以上,ローレンツアトラクタを描くために,いくつかのパラメータがありますので整理しておきましょう。
(1) 微分方程式の係数
ローレンツの著書の中では,b=8/3,σ=10,r=28 としています。冒頭に挙げたMathematica のサンプルではこれとは異なる値になっています。
(2) $${(x,y,z)}$$ の初期値
他の著書にあるように,(10,12,15)が多いようです。山口昌男の著書には「平衡点」が示されています。 原点のほかに2つあります。
(3) 時間ステップ
ローレンツの著書で「小数点の位置を間違えた」と書かれている微小な値です。
(4) 繰り返し回数
相空間に打つ点の数です。
これらのパラメータのうち,微分方程式の係数以外をインタラクティブに変えられるものを次のページに載せました。
リンク先を開くと,次の画面になります。

・左の円形スライダで視点を変える(軸回りに回転)することができます。
・係数 s, r, b は固定です。これを変える場合は,HTLMのソースの中に,CindyScript の部分があるので,そこで変えることができます。
・初期位置を平衡点にすると,これは動かない点なので最初の小さな点だけが表示されます。しかし,初期位置増減スライダでほんのわずかだけ変えてやると,アトラクタが現れます。バタフライ効果です。
・Δt のボタンは,ローレンツの著書で「小数点の位置を間違えた」と書かれている値に変更するものです。
いろいろとパラメータを変えてみましょう。
