
Cinderellaでカオスを描く:ロジスティック写像
ロジスティック方程式
17世紀に始まった人口の増加率に関する問題について、18世紀のマルサスの研究を経て、19世紀になってベルハルストが次のように定式化しました。
人口の増加率を $${\dfrac{dN}{dt}}$$ とすると $${\dfrac{dN}{dt}=\dfrac{r}{K}(K-N)N}$$ となる。
これをロジスティック方程式といいます。人口や生物の個体数は整数値ですが、これを連続的な変数とすると、この式は微分方程式であると考えられます。この微分方程式は、解析的に(つまり式変形と積分で)解くことができて、
$${N(t)=\dfrac{KN_0 e^rt}{N_0 e^rt+K-N_0}}$$
となります。$${N_0}$$ は初期値です。
このあたりの詳細は、山口昌哉著の「カオスとフラクタル」(1986年ブルーバックス、2010年ちくま学芸文庫)に書かれています。
この解のグラフを描くと次のようになります。これをロジスティック曲線といいます。グラフを描くのは簡単ですので、スライダで初期値や係数$${K,r}$$を帰られるようにしました。
リンク先を開くとつぎの画面になります。

スライダを使って値を変えてみましょう。

このロジスティック方程式については1940年代の内田俊郎、森下正明(ともに京都大学)らの研究を経て、1973年のロバート・メイの式に至るのです。1970年代は電卓がポケットサイズとなり普及した時期です。
差分方程式
微分方程式を次のようにして近似化することを差分化といい、それによって得られる式を差分方程式といいます。
まず、微分の定義を思い出してください。xがtの関数であるとき、微小な変化量Δt、Δxを用いると $${\displaystyle{\dfrac{dx}{dt}=\lim_{\Delta t \rightarrow 0} \dfrac{\Delta x}{\Delta t}}}$$ と定義されます。$${\Delta t}$$ が0に近い値であれば
$${\dfrac{dx}{dt}=f(t)}$$ のとき $${\dfrac{\Delta x}{\Delta t}=f(t)}$$
と近似できますので,$${\Delta x=x_2-x_1}$$ とすると $${x_2=x_1+\Delta t f(t)}$$ となります。そこで,微分方程式のロジスティック方程式 $${\dfrac{dN}{dt}=\dfrac{r}{K}(K-N)N}$$ において $${\Delta N=N_{n+1}-N_n, \ a=(1+r \Delta t), \ \dfrac{r \Delta t}{K(1+r \Delta t)}N_n=x_n}$$ とすると $${x_{n+1}=a(1-x_n)x_n}$$ を得ることができます。
これをロジスティック写像といっています。
ロジスティック写像のリターンマップ
ロジスティック写像の式において、初期値 x1 から出発してx2,x3,・・・と順次求めていきます。
たとえば a=1 のとき、初期値を x1=0.1 とすると 0.1 0.09 0.0819 0.0752 ・・・ となっていき、ある値に収束します。
この様子を調べるために、簡単なスクリプトを書いて実験してみましょう。
----------------------------------------------------------------------
a=1;
f(x):=a*x*(1-x);
x=0.1;
repeat(20,
print(x);
x=f(x);
); ---------------------------------------------------------------------
aと最初のxの値をいろいろ変えてみると、数の変化がわかります。repeat の回数を増やせばわかりやすいかもしれません。(Pythonなどでは for の繰り返し)
a=3.2 x=0.2 のときを調べてみると
0.2 0.512 0.7995 0.5129 0.7995 0.513 0.7995 0.513 0.7995 0.513 ・・・
となり、2つの値を繰り返します。この状態を「周期が2である」といいます。
さらに、a=3.5 x=0.2 のときは、はじめのうちはばらばらに見えますが、repeatの回数を50くらいすると、4つの値が繰り返されるようになります。「周期が4」となるのです。(実際に試してください)
ところが、a=3.5 x=0.2 のときは、まったくばらばらで周期性が見えません。
さて、数値の並びだけではわかりにくいので、これを図で表すことにします。これをリターンマップといいます。
ポイントは、あるxの値から次の値を図形的にどう取るかということなのですが、ここで直線 y=x がうまい役割をします。
次の図を見てください。
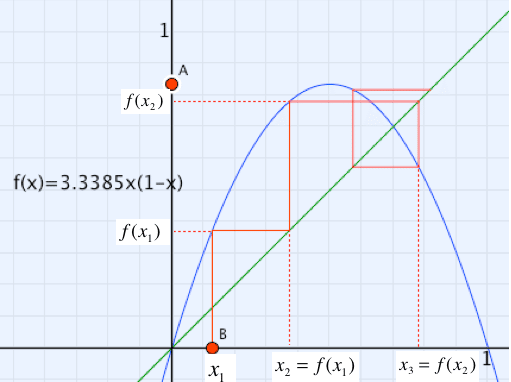
点Bが初期値を示します。それに対する $${f(x)=ax(1-x)}$$ の値 $${f(x_1)}$$ が、放物線 $${y=ax(1-x)}$$ 上の点のy座標です。(図では a=3.3385)
ここから横に線を引いて、直線 $${y=x}$$ との交点を求めると、そのx座標が $${f(x_1)}$$ となります。これが $${x_2}$$です。
$${x_2}$$から$${x_3}$$を求めるのも同様です。
すなわち、x軸上の$${x_1}$$から出発して、放物線->直線->x軸 と戻ってくれば次の値をx軸上に求めることができるわけです。
上図で、y軸上の点Aを動かすと、係数aの値を変化させることができます。次のリンク先を開いてみましょう。
次の図は先ほど示した、周期が2,4になるときの図です。周期性の意味が図から読み取れるでしょうか。リンク先を開くと左側の図になります。この図では、上図に加えて、x1,x2,x3・・・の点列を緑の点でx軸上に示しています。

右側の図はちょっと読みにくいですね。数値は確かに4周期を示していますが。
点A,Bをドラッグして値を変えてみましょう。
ロジスティック写像の分岐図
今までは、a=3.2やa=3.5でした。初期値は $${x_1=0.2}$$ でしたが、$${x_1=0.3}$$ としても実は同じ結果になります。同じ結果という意味は、初期値が異ってもずっと先の方に行くと同じ値に収束したり、周期性を示したりするということです。
ところが、a=3.57・・・ を超えると、初期値によって値の動きはまったく異なるものとなるのです。(これもやってみましょう)これを「初期値鋭敏性」と言います。そして、a=4に十分近いとき、カオスになるのです。
aの値によって、xの値は収束したり、周期的になったりします。この様子を次のように図(グラフ)にします。
今度のグラフは、横軸にaの値、縦軸にxの値を取ります。そして、各aの値に対する点列 $${x_1,x_2,x_3,}$$・・・・ をプロットしていくわけですが初めの方は省略します。なぜかというと、上の周期4の図を見てください。初めの方は値がばらつくために、いろいろな線が出ています。あとのほうだけをとればはっきり周期性がわかります。このようにして作ったのが見出しの図です。再掲しましょう。

この図では、はじめの100個をパスしてあとの100個を表示しています。aの値は0から4まで、4000等分しています。プログラムは次の通りです。
f(a,x):=a*x*(1-x);
a=0;
x0=0.1;
repeat(4000,
a=a+0.001;
x=x0;
repeat(100,x=f(a,x));
repeat(100,
x=f(a,x);
draw([a,x],size->0.05);
);
);
// a軸目盛表示
apply(0..4,drawtext([#-0.02,-0.07],#,size->16));リターンマップで実験したように、a=1までは0に収束し、1から3まではある値に収束します。前述のように、はじめの100個はパスしていますので、線が1本ということは値が一つ、つまりある値に収束しているということです。3を超えたところで2つに分岐しますね。これは2周期になっているということです。さらに4周期になり、8周期になり・・カオスになります。ただ、しばらくいくと、白く抜けるとことがあります。これを「窓」といっていますが、ここでは3周期になっています。なお、「カオスになる」というのは、「収束しない」「初期値鋭敏性がある」ということなのですが、数学的にはリー・ヨークの定理とそれによる証明をすることになります。興味がある人は調べてみてください。
リターンマップを作る
このあとは,Cinderella でロジスティック写像のリターンマップを作る手順を説明します。
まず、座標平面の設定をします。
(1) 下のツールバーの「座標軸を描く」「グリッドを描く」「グリッドにスナップする(磁石アイコン)」をクリック。
(2) 拡大ツールで1目盛が0.1になるように拡大します。
(3) 「点を加える」モードで点Aと点Bをとります。場所は適当。あとからx軸とy軸の上に乗せます。
(4) 「直線を引く」モードで、背景のx軸、y軸に重なるように直線を引きます。

(5) インスペクタで線の色を黒に、「ラベルをつける」のチェックをはずします。
直線を引くのに使った4点(C,D,E,F)は非表示にします。(「表示する」のチェックを外す)
(6) 「点の取り付け/取り外し」モードにして、点Aをy軸に、点Bをx軸上に乗せます。これで、点Aはy軸上のみを、点Bはx軸上のみを動かせるようになります。
これで座標平面の設定は終わりです。CindyScript エディタを開いてスクリプトを書きます。
ロジスティック写像の式は次の通りです。(再掲)
$${x_{n+1}=a x_n(1-x_n))}$$
手順を示しますので書いてみてください。(あとで例を示します)
(1) aの値をy軸上の点Aのy座標で決めます。点Aが放物線の頂点のy座標になるようにしますので,a=4*A.y とすればよいでしょう。
(2) 2次関数 $${f(x)=a*x*(1-x)}$$を定義します。
(3) (2)で定義した2次関数のグラフ(放物線)を plot 関数で表示します。
(4) 直線 y=x をplot 関数で表示します。色を濃い緑にでもしておきましょう。
(5) drawtext関数を使って,適当な場所に、2次関数の式を表示します。係数aの値は点Aの動きにつれて変化するようにします。文字列の結合を使って
"f(x)="+a+"x(1-x)" とすれば a のところは点Aのy座標になります。
(6) x軸上に目盛の数字1,y軸上にも目盛の数字1を表示します。
(7) xの初期値を点Bのx座標にします。y座標の初期値は0にします。
(8) 繰り返し数を変数として用意します。例えば n=10。初めはこのくらいの小さな値にしておき,動作を確かめたら大きくします。
(9) linecolor関数を用いて、これから描く線の色を赤に設定します。(他の色でももちろんかまいません)
(10) repeat 文で,「関数値を計算し、線を引き、次の値として引き渡す」、という作業をn回繰り返します。ここがスクリプトの中心になります。
[1] 出発点と、放物線上の点を直線で結び (出発点の最初は点Bです)
[2] 放物線上の点から直線 y=x に水平線を引き
[3] 次のxの値を関数値とし、これをそのままy座標として次の出発点とします。
少しわかりにくいかと思いますが、出発点の座標を書いていくとつぎのようになります。
うまくいけば次のような図が描けます。

うまくいったら,nの値を大きくしましょう。
スクリプトの例です。
a=4*A.y;
f(x):=a*x*(1-x);
plot(f(x));
plot(x,color->[0,0.5,0]);
drawtext([-0.5,0.5],"f(x)="+a+"x(1-x)",size->16);
drawtext([0.98,-0.06],1,size->16);
drawtext([-0.04,0.98],1,size->16);
x=B.x;
y=0;
n=10;
linecolor([1,0,0]);
repeat(n,
draw([x,y],[x,f(x)]);
draw([x,f(x)],[f(x),f(x)]);
x=f(x);
y=x;
);リターンマップで実験
点Aと点Bを動かすと,係数$${a}$$ と,初期値を変えることができますが,直接指定することももちろんできます。たとえば a=3.2; x=0.2; としてみましょう。どうなりますか。
また,println(x) を repeat ループの中にいれて数値を表示してみましょう。println(guess(x)) や println(format(x,12) ) のようにすると小数点以下の桁数が増えます。このとき,a の値と初期値によって,周期性があらわれることがあることがわかります。8周期、16周期は、50回くらい繰り返したのではわかりません。200回くらいで見つかります。また、4桁表示では8周期に見えても(緑の点も8つ)16位までの表示では周期的になっていないこともあります。
前述の「ロジスティック写像の分岐図」のところで説明したことを実際に確かめてください。
