Cinderellaでカオスを描く:合成写像のカオス
2つの関数の合成写像(関数)を描きます。
(1) $${x_{n+1}=y_n+a x_n+\dfrac{5}{1+(x_n-10)^2}}$$
$${y_{n+1}=- x_n}$$
(2) $${x_{n+1}=y_n+a x_n-\dfrac{5}{1+(x_n+10)^2}}$$
$${y_{n+1}=- x_n}$$
まず(1) で変換し,それを(2)で変換した値をプロットします。「カオスCGコレクション」(川上博著:サイエンス社:以下「この本」)には,次の例が示されています。

これについて,
この例では $${f(x)}$$ の選び方を,$${f(x-10)}$$ , $${f(x+10)}$$ のように2つの写像でずらしてあるので原点付近は閉曲線群となり,円環状カオスが見られる。また,両式ともパラメータ$${a}$$ を同じに選んだのであまり合成写像の効果はなく,1つの写像
$${x_{n+1}=y_n+a x_n+\dfrac{5}{1+(x_n-10)^2}-\dfrac{5}{1+(x_n+10)^2}}$$
$${y_{n+1}=- x_n}$$
と定性的に変わらないカオスとなっている。
と説明されています。ここに示されているのが「式(2.22)」なのですが,「定性的に変わらない」の意味がよくわからないので,実際に両方を表示して比較してみましょう。
リンク先を開くと次の画面になります。

左上のボタンで,合成写像(関数)と関数2(式2.22)が選択できます。
初期状態は合成関数で,原点付近に閉曲線が描かれています。
このまま係数を変化させていきますが,ずっと閉曲線のままでしょう。しかし,$${a=-1.96}$$ と $${a=1.85}$$ のところで突然カオスが現れます。ただし,いままでやったように,縦横比を調整する必要があります。


この本に掲載されている $${a=-0.04}$$ では,閉曲線のままで掲載図のようにはなりません。何が違うのでしょうか。
実は,初期値が違うのです。
$${a=-0.04}$$ にしたのち,初期値の赤い点を動かしてみましょう。原点付近ではどこに持っていっても閉曲線のままです。原点から遠ざけていくと突然カオスが現れ,この本の左上の図のようになります。

初期値の点をわずかにずらすと,およその形状は同じでも色合いが変わったり,複数の閉曲線ができたりします。
ではこの状態で,係数を本に掲載されている右上の$${a=-0.02}$$ にしてみましょう。2つの閉曲線になってしまいましたか。
さらに初期値を原点から遠ざけると次のように掲載図に似た形になります。

次の掲載図$${a=0.01}$$ にしてみましょう。やはり閉曲線になったでしょうか。初期値を変えれば掲載図のようになります。
この初期値については,本ではまったく触れられていません。
では,合成関数と関数2の比較をしましょう。係数は$${-0.07}$$です。まず左上の「関数2」をクリックし,係数を $${-0.07}$$ にして初期値の点を移動し,掲載図になる場所を探します。(下図右)その状態で「合成関数」ボタンをクリックします。(下図左)

「定性的に変わらない」が同じような形状になる,ということではないようです。しかし,$${a}$$ の値と初期値によっては同じような形状になることもあります。それらを探索するのは,面白いのではないでしょうか。$${a}$$ の値と初期値を変えてみて,合成関数と関数2のボタンを交互にクリックしてみましょう。
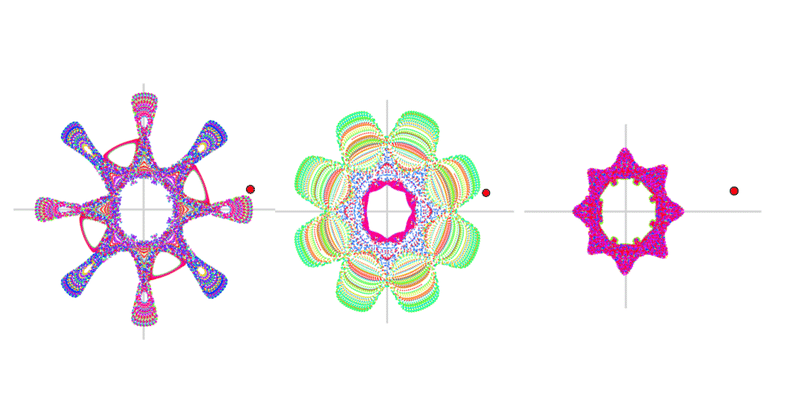
見出し画像は,$${a}$$ の値を 0.01 だけ変化させたときにコロコロと図が変わる様子を示しています。また,これらの場合は合成関数と関数2では同じような形状になります。どこにあるのか,探してみてください。
←前節:円環状カオスと閉曲線群
→次節:強制系のカオス
