
Cinderellaで数学:2次関数の最大値と最小値
2次関数には限りませんが、グラフを描くと定義域に対する値域をグラフから読み取ることができます。
値域のなかに、最大になる値があればそれを最大値とします。いくらでも大きい値がある場合や、値域が大きい方の値を含まない場合は最大値はありません。最小値についても同様に考えます。
定義域・値域と最大値と最小値の問題として,次のパターンがあります。
(1) 定義域の幅が変わる
$${f(x)=x^2-2x}$$ ( $${0 \leqq x \leqq a}$$ )のようなパターン
(2) 定義域の幅が一定で変化する
$${f(x)=x^2-2x}$$ ( $${a \leqq x \leqq a+2}$$ )のようなパターン
(3) 定義域は一定で,2次関数が変化する
$${f(x)=x^2-2ax+1}$$ ( $${0 \leqq x \leqq 2}$$ )のようなパターン
(4) 定義域,関数とも変化する
$${f(x)=x^2-2ax+a^2+2a-1}$$ ( $${0 \leqq x \leqq 1-a,a<1}$$ )のようなパターン
それぞれ,Cinderella の作図機能も使いながらインタラクティブに動かして考えるアプリケーションを作ります。
(1) 定義域の幅が変わる
【例】$${f(x)=x^2-2x}$$ ( $${0 \leqq x \leqq a}$$ )
グラフを描くときに,定義域の範囲だけ描くのが基本ですが,グラフ全体も点線で示しておくのが普通です。
まず,作図ツールの「直線を加える」を使ってx軸とy軸を引いておきます。磁石ツールで背景の方眼を表示し,格子点にスナップするようにしておくのがよいでしょう。作図に使った点はインスペクタで非表示にし,点や線のラベルも非表示にしておきます。
次に,「線分を加える」ツールで,原点からx軸上の適当なところまで線分を引きます。点が直線上だけを動くようになっていることを確かめましょう。また,インスペクタで色や太さを変え,ラベルは非表示にしておきます。次の図では,背景色も白にしています。
スクリプトエディタを開いてDrawスロットにプログラムを書きます。
$${f(x)}$$ を定義して,全体を点線で,定義域の分を実線で描きます。点線は修飾子の dashtype を使います。定義域の右端の点の上に a を表示しておきましょう。
方眼については,高校の数学では描かないのが普通なので,背景の方眼を非表示してもいいのですが,スナップ機能があるほうが操作性がいいのでそのままにしておきます。目盛の数字は必要なところだけ入れます。原点のOは,点のラベルを O にして表示し,Shift キーを押しながらドラッグして左下に移動しました。
f(x):= x^2 - 2*x;
a = F.x;
plot(f(x), dashtype -> 3);
plot(f(x), start -> 0, stop -> a, size -> 2);
drawtext([F.x - 0.2, 0.5], "a", size -> 16);
drawtext(F.xy - [0.2, 1], a, size -> 16);
drawtext([-0.2, f(a)-0.2],f(a), align -> "right", size -> 16);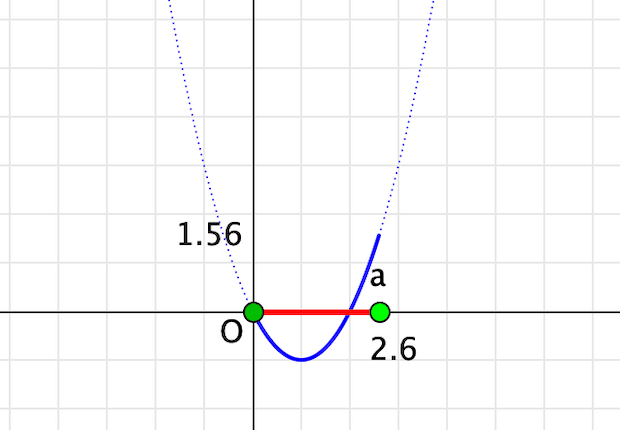
定義域の右端の点をドラッグすれば,最大値を読み取ることができます。
(2) 定義域の幅が一定で変化する
【例】$${f(x)=x^2-2x}$$ ( $${a \leqq x \leqq a+2}$$ )
作図ツールで(1) と同様に作図をしておきます。定義域は左右とも可変なので,原点にとらないように注意します。(1) の例では原点(x軸とy軸の交点)にとったので,固定点になり,色も暗い色になっています。
(1) と違うのは,定義域の左の点の x 座標を a とすることです。
f(x):= x^2 - 2*x;
a = E.x;
F.x = a + 2;
plot(f(x), dashtype -> 3);
plot(f(x), start -> a, stop -> a + 2, size -> 2);
drawtext([E.x - 0.1, 0.2], "a", size -> 16);
drawtext([F.x - 0.4, 0.2], "a+2", size -> 16);
drawtext(E.xy - [0,0.5], a, align -> "mid", size -> 16);
drawtext(F.xy - [0,0.5], a+2, align -> "mid", size -> 16);
drawtext([-0.2, f(a)-0.1],f(a), align -> "right", size -> 16);
drawtext([-0.2, f(a+2)-0.1],f(a+2), align -> "right", size -> 16);次の図では,拡大ツールを使って全体を少し拡大しています。定義域の範囲が2と一定で狭いためです。
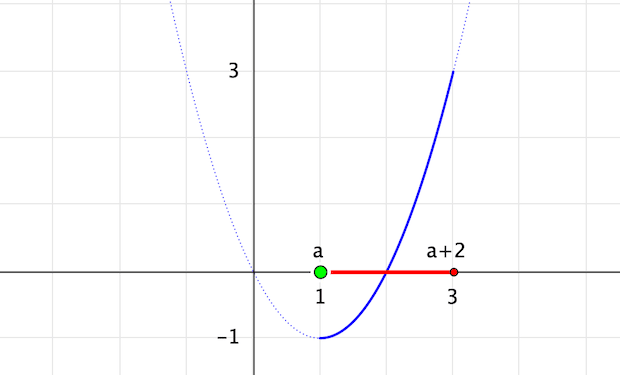
(3) 定義域は一定で,2次関数が変化する
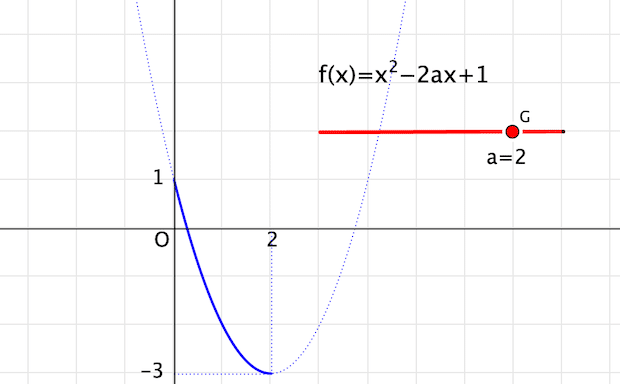
【例】$${f(x)=x^2-2ax+1}$$ ( $${0 \leqq x \leqq 2}$$ )
画面の作図は(1),(2)と同様ですが,定義域は変化しないので,定義域を描いている線分EFをx軸上に置いておく必要はありません。他の場所に移して、係数aを変化させるスライダとして使いましょう。今はx軸にインシデントとなっているので,「点の取り付け取り外し」ツールで軸上から外します。線分EF上に点をとっておきます。線分EFの幅を5,その点をGとして,a = G.x - E.x - 2 とすれば,係数 a を $${-2 \leqq a \leqq 3}$$ の範囲で変化させることができます。このとき,あまり細かい変化をさせるより,0.1 ごとの方が使いやすいでしょう。
a = round((G.x - E.x - 2)*10)/10
とすれば,0.1 ごとにaを変化させることができます。このとき,磁石ツールで格子点へのスナップは解除しておくほうがよいでしょう。
その他,$${f(2)}$$に対応するグラフ上の点と両軸への垂線を点線で描いておくと数値の対応がわかりやすくなります。
f(x):= x^2 - 2ax + 1;
a = round((G.x - E.x - 2)*10)/10;
plot(f(x), dashtype -> 3);
plot(f(x), start -> 0, stop -> 2, size -> 2);
drawtext(G.xy - [0.1, 0.7], "a=" + a, align -> "mid", size -> 16);
drawtext([-0.4, -0.4], "O", size -> 16);
drawtext([1.9, -0.4], 2, size -> 16);
drawtext([-0.2, f(0)-0.1],f(0), align -> "right", size -> 16);
drawtext([-0.2, f(2)-0.1],f(2), align -> "right", size -> 16);
drawtext([3, 3],"$f(x)=x^2-2ax+1$", size -> 18);
draw([[2, 0],[2, f(2)]], dashtype -> 3);
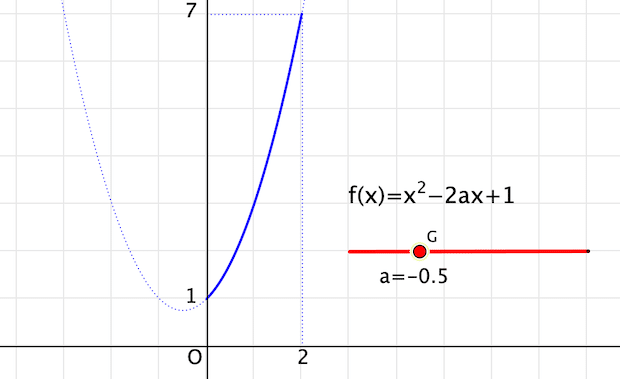
draw([[0, f(2)],[2, f(2)]], dashtype -> 3);(1)(2) はグラフが動かないので比較的イメージしやすいのですが,今度はグラフが動きます。その動きをイメージできるかどうかが鍵になるので,スライダで動かしてみて,グラフがどのように動いていくかを体験するのが肝要です。紙と鉛筆だけではなかなかできないことです。
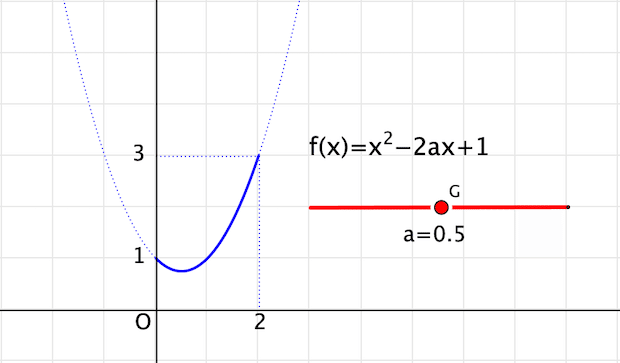
(4) 定義域,関数とも変化する
【例】$${f(x)=x^2-2ax+a^2+2a-1}$$ ( $${0 \leqq x \leqq 1-a, a<1}$$ )
定義域だけでなくグラフの位置も変わるので一番難しいパターンです。ここまでやった3つの例題に共通するポイントは何でしょう。最大値・最小値の候補は、x 座標が定義域の端点と頂点のときです。そして、場合分けの分かれ目は頂点の位置、言い換えると軸の位置です。
では作図します。画面設定は(3)と同様ですが,定義域を示す線分をx軸上に作図しておきます。線分HKになったとします。(Hは原点) K.x = 1 - a とすれば,定義域の右端が決まります。
f(x):= x^2 - 2ax + a^2 + 2*a-1;
a = round((G.x - E.x - 4)*10)/10;
K.x = 1 - a;
plot(f(x), dashtype -> 3);
plot(f(x), start -> 0, stop -> 1 - a, size -> 2);
drawtext(G.xy - [0.1, 0.7], "a=" + a, align -> "mid", size -> 16);
drawtext([-0.4, -0.4], "O", size -> 16);
drawtext([1.9, -0.4], 2, size -> 16);
drawtext([-0.2, f(0)-0.1],f(0), align -> "right", size -> 16);
drawtext([-0.2, f(2)-0.1],f(2), align -> "right", size -> 16);
drawtext([3, 3],"$f(x)=x^2-2ax+a^2+2a-1$", size -> 18);
draw([[2, 0],[2, f(2)]], dashtype -> 3);
draw([[0, f(2)],[2, f(2)]], dashtype -> 3);スライダを動かすと,放物線の位置,定義域の両方が動きます。
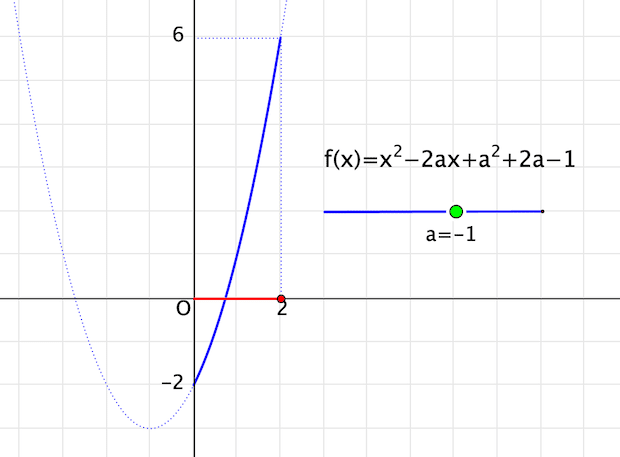
最大・最小が変わる境目はこのあたりでしょう。
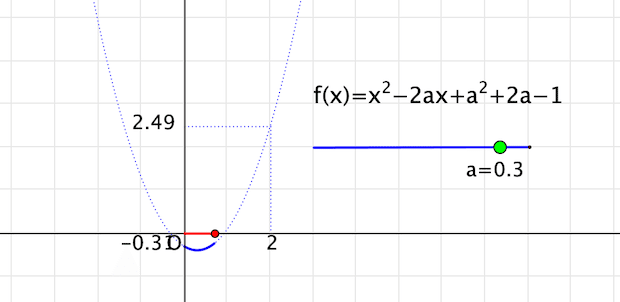
実際には計算で求めないと正確にはわかりませんね。しかし,ここで大切なのは「動かしてみる」ということであり,それが頭の中でできるようになるということです。
