
【統計の勉強】統計量Zとは?
こんにちは。日々の実験データを論文レベルのものにしようとR言語と統計を勉強している、生命科学系研究者のえいこです。
最近は少しずつ、統計の勉強をまともにしようと思っています。(基本的に机に向かってのお勉強は苦手なので、必要に迫られたらやるタイプ)
以前は同じ日本語なのに眠たくなるくらい何が書いてあるかわからなかった統計関連の解説が、少しだけわかるようになってきました。
やっぱり少しずつでも勉強し続ける、その分野の単語に触れ続けると言うのは大切ですね。
で、今回は統計量Zについてちゃんと勉強してみようと思います。
そもそも統計量ってなに?
t検定とかTukey-Krammerとか検定をたくさん使っている割には”そもそも”の検定の考え方、「統計量」というのが、ちょっと理解が曖昧...
Wikipediaで調べてみると、
標本データに目的に応じた統計学的なアルゴリズム(関数)を適応して得た、データの特徴を要約した数値のこと。
日本産業規格では「確率変数だけで規定された関数」と定義している。
なんのことだかさっぱりわかりません。
たとえば、一番身近な統計量は算術平均です。(要は平均を取る)
全てのデータの数値を足して、データの数で割る
(この計算がアルゴリズム)
統計学的には、対象とするデータは母集団から抽出される、(一部の)標本であり、標本から直接算出される「統計量」は、標本の取り方によっていつでも変わるもので、標本を特徴付ける数値となります。
全てのデータを見ることはできないのですが、母集団(全てのデータ)と母数によって特徴付けられる確率分布として仮定して、そこからあるサイズの標本をランダムに取り出して検定してものをいう訳です。
統計量の種類にはいくつかあります。
・要約統計量(標本の性質を要約するための統計量)
正規分布の場合は平均、分散、標準偏差
正規分布から著しく外れた場合は、中央値、四分位点、最大値、最小値、最頻値が使われる
・検定統計量(統計学的検定に利用するために標本から算出する統計量)
パラメトリックにおいては、尤度比が最小十分統計量となる
なにを検定したいのかによって検定統計量を選ぶ(Z, t, χ2, F, U)などなど...
・順序統計量(標本を値の大小で並べたときの順序)
要はランク統計量でノンパラメトリック統計学でよく使われる。最小値、最大値、中央値、分位など。
今回調べたい統計量Zは、「検定統計量」に分類されます。
統計的な検定では、データから算出された検定統計量よりも極端な値を取る確率が有意水準と比較して大きいのか小さいのかに基づいて帰無仮説を棄却するかどうかを判断します。
(統計の時間より)
統計量の基本的な考え方は、「データを元に算出する代表的な値」と覚えておくと良いかもしれません。
統計量Zとは?
平均が0、分散が1となるようにデータを変換したもの。(標準化)
例えば、標本平均を標準化した値は次の計算式で表します。

この統計量Zは標準正規分布に従うので、Zを用いた検定を行うには標準正規分布を使います。
数式で表されても...という感じ。(数式にめっぽう弱いので...)ただ分子は平均を0に、分母は分散を1にする操作をしている感じがします。
統計量Zを使うZ検定は、母平均、母集団の標準偏差がわかっていないと使えないので、実用的ではないというのが実際のところ...
Wilcoxon検定の時にZ値を出すのはなぜ?
この統計量Zはノンパラメトリック二群検定(Wilcoxon検定を使った)の時の効果量を計算する時に出てくるのです。
ではなぜ、Wilcoxon検定で統計量Zを算出するんでしょう?
通常はWilcoxon検定の時は統計量Tを計算します。
統計量Tは統計量Wと統計量wを比較してその値が小さい方がTとなります。統計量WはXi>Yiが満たされる時の順位の合計値、統計量wはXi<Yiが満たされる時の順位の合計値。
T値がWilcoxonの符号順位検定表における棄却限界値以下の時に帰無仮説を棄却し、2群間の母代表値に差があると結論づけます。
でも、N(二群の合計のサンプル数)が25を越える場合は統計量Zを考えて統計処理を行います。

こんな感じの数式を使って標準化してTの分布を正規分布に近似します。
サンプル数が25を越える場合は、統計量Zを使って統計処理をしますが、効果量を計算する時にはサンプル数に関係なく統計量Zを使って計算します。
※なぜサンプル数が25以上なのかは理由はよくわかりません。多分、数式を見たらわかるものなんでしょうけど...
ノンパラメトリックの時の効果量と統計量Z
Wilcoxon検定の時の効果量はZ/√Nで計算します。で、√Nで割るとN(サンプルサイズ)の影響が出てしまうのではないかと、ずっと疑問だったのです。
が、今回Zの計算式を見て√Nで割ることはサンプル数の影響を取り除いているということに気がつきました。
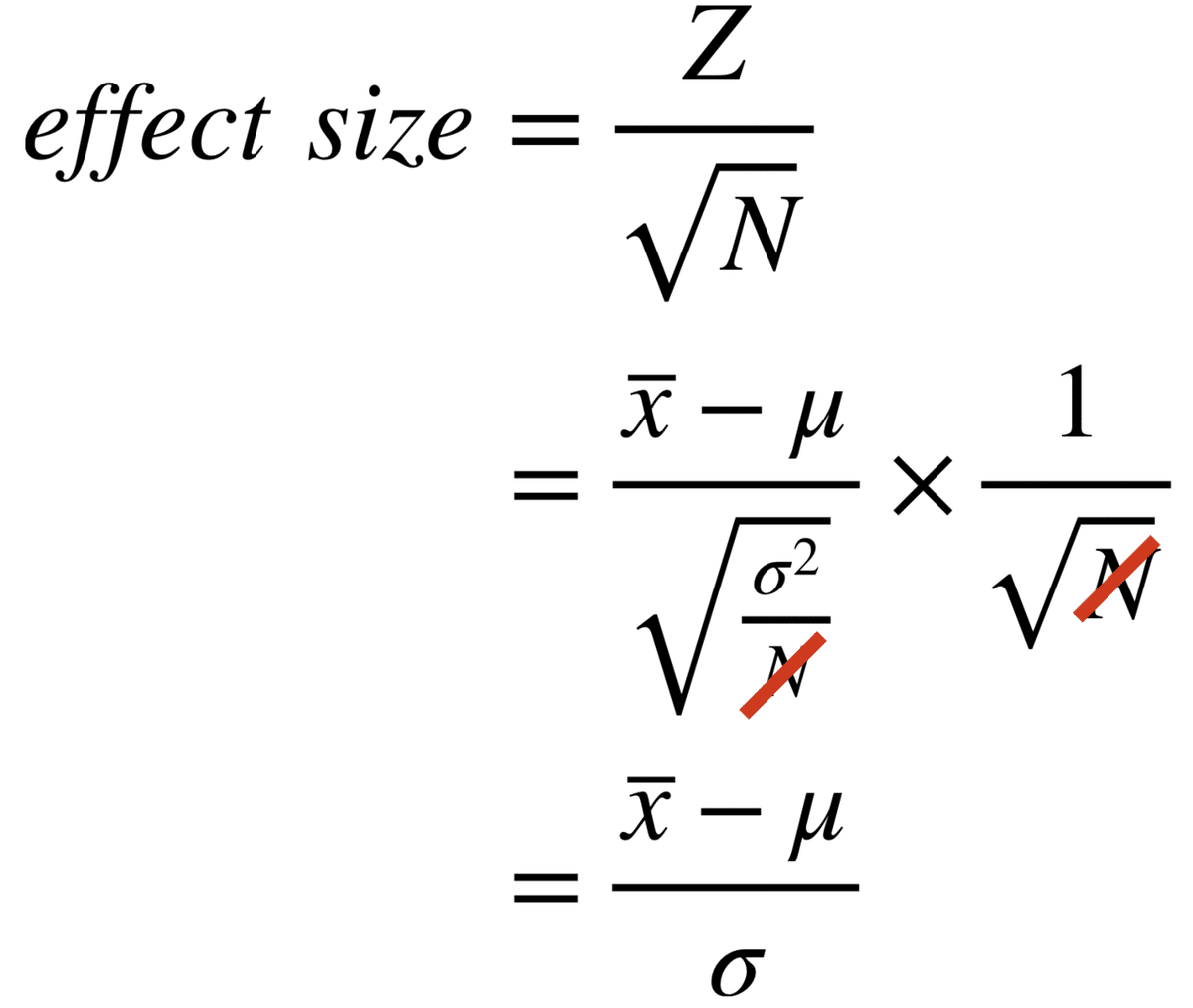
こんな感じで、効果量はデータの平均値、母集団の平均値、母集団の標準偏差(ばらつき)のみで表せました。
この辺で、統計量Zの勉強は一区切りにしようと思います。
ここでのまとめは、
・統計量Zはデータを平均を0、分散を1にした時の統計量で、確率検定に用いる
・ノンパラメトリックの場合の効果量の計算の時に√Nで割るのはサンプル数の影響をなくすため
それでは、また!
今回初めて数式をTeXで書いてみたのですがキレイですね!機会があれば、「初心者がTeXを触ってみた」という内容で記事を書いてみようと思います。
記事、書きました↓
参考文献
いいなと思ったら応援しよう!

