
Google Colabで統計的因果探索手法LiNGAMを動かしてみた
電通デジタルでデータサイエンティストをしている中嶋です。
前回の記事は「Airflow 2.0でDAG定義をよりシンプルに!TaskFlow APIの紹介」でした。
Advent Calendar 10日目となる本記事では因果探索の一手法であるLiNGAM(Linear Non-Gaussian Acyclic Model)の解説及び、Google Colabでの分析例について紹介します。
因果探索とは
最近のトレンド
最近、広告配信やマーケティング分析の文脈で施策の効果を適切に評価する手法として実験計画法や因果推論が注目を浴びています。産業界でも株式会社ソニーコンピュータサイエンス研究所、クウジット株式会社、株式会社電通国際情報サービスの三社が提供するCALCという要因分析ツールや、最近はNECの因果分析ソリューション causal analysisも出ていたりと盛り上がりを見せています。今回紹介するLiNGAMは因果探索という少し違うテーマの分析手法ですが今年の第23回IBISML(情報論的学習理論ワークショップ)のチュートリアルセッションでも統計的因果探索が扱われており、統計的因果推論と合わせて今後ますます注目度が高くなっていくと考えられます。
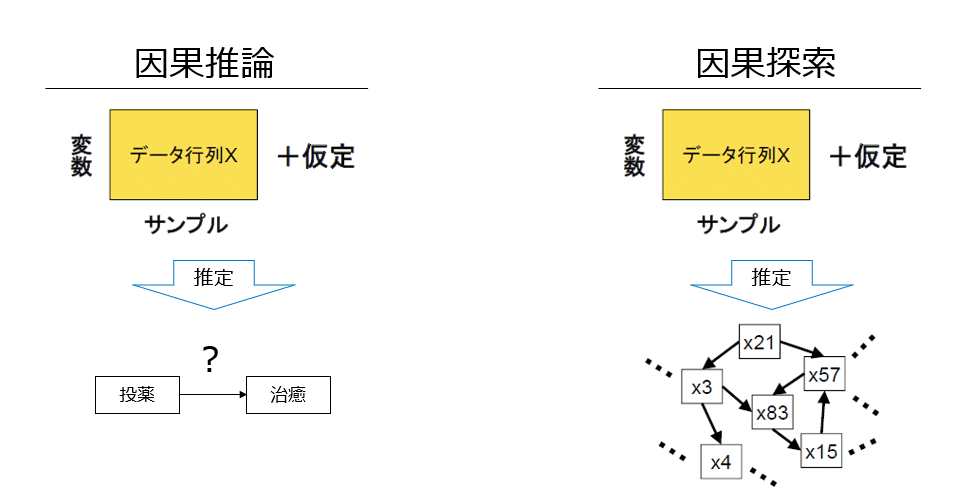
因果推論と探索探索
因果探索とは、効果検証や因果推論のような特定の変数同士の因果関係を調べる仮説検証的分析の文脈ではなく、探索的データ分析の文脈でそもそもどんな因果関係が起きているかを調べるための手法となります。因果推論では下記のように推定したい因果の組み合わせが予めわかっているような状況を想定します。例えば投薬とそれによる病気の治癒の因果関係などがあります。一方、因果探索ではそのような知りたい因果仮説を置かずに観測されたデータから全体の因果構造の推定を行います。データの構造そのものを把握したい場合にはもちろん使えますが、データに関する背景知識が全くない場合に因果探索のアウトプットを仮説として因果推論につなげていくような用途も考えられます。
構造方程式モデル
具体的な因果探索手法の話に入る前に、因果探索において使われる構造方程式モデルという考え方について説明します。
統計的因果探索ではこの構造方程式モデルを用いてデータの生成過程を方程式としてモデル化して、因果構造を考えるベースとしています。
具体的に2変数の場合の構造方程式は下記のように書けます。

ここで式の左辺に出てくるx,yは内生変数と呼び、観測変数を表します。右辺に出てくるexやeyのことを外生変数と呼び、観測されない変動要因などを表します。上記の右図はパス図と呼び、因果関係を矢印と変数を使って図で表現したものです。ここでは例としてexとeyに相関があり未観測共通原因の存在を仮定していますが、以後の説明では未観測共通原因が無い場合を想定しています。
また、fyは観測変数間の関係を表す関数です。特に定まった呼称はないようですが、この記事では以後、関数形と呼びます。
構造方程式に出てくる等号は通常の等号とは少しニュアンスが異なり、もちろん左辺と右辺が等しいという意味ではありますが、右辺から左辺へデータが生成される過程を表しているものと考えます。
次で述べるように統計的因果探索の分野ではこの外生変数の分布と関数形をどう仮定するかで3種類のアプローチが考えられています。
仮定の違いによる因果探索手法の分類
因果探索手法は今回紹介するLiNGAM以外にも、モデルにおく仮定によって3種類のアプローチに分けられます。最初に3つのアプロ―チの違いについて下記の表にまとめます。

- ノンパラメトリックアプローチ
このアプローチでは外生変数の分布や関数形に特別な仮定を置かずに因果的マルコフ条件という仮定を置いて因果グラフの候補を探索します。
・因果的マルコフ条件
因果的マルコフ条件とは、観測変数それぞれがその親となる変数で条件付けた場合、条件付独立になるという条件です。変数xiの親変数群をpa(xi)として式で書くと下記のようになります。

通常はデータから因果グラフを一意に推定することができないため、同じデータから導かれる複数の因果グラフ候補の探索が目標となります。ちなみにデータから一意に因果グラフが定まることを識別性があると言います。
このアプローチの詳細は参考文献[1]のP74以降をご参照ください。
- パラメトリックアプローチ
このアプローチでは外生変数の確率分布と関数形に特定のものを仮定して因果探索を行います。直感的には条件が追加されたことで因果グラフを一意に特定できそうな気がしますが、ガウス分布に従う外生変数で関数形が線形の場合は一意に特定することができません。
具体的に下記のような2変数の例を考えてみます。

因果の方向は逆になっていますがそこから生成されたデータの分布はどちらもほぼ同じ形をしており、この分布から変数の因果順序を正しく推定することはできません。このようなケースがあるため因果モデルの一意推定はできませんが、代わりに平均因果効果(ATE)を推定する方法が研究されています。これも詳細は参考文献[1]のP81以降をご参照ください。
- セミパラメトリックアプローチ
このアプローチでは外生変数の確率分布には仮定を(ほぼ)おかず、関数形に線形性を仮定します。特にこの後説明するLiNGAMはこのアプローチに属する手法です。
この手法では非ガウスな分布に従う外生変数を仮定するところが個人的にはミソだと考えています。詳細は参考文献[1]P92以降をご参照いただきたいのですが、イメージとしてはガウス分布特有の「変数同士が無相関⇔独立である」という性質がなくなることで、独立成分分析を使ったときに独立成分をうまく識別でき、それによって因果グラフを理論上は一意に特定することが可能となります。
・独立成分分析(どくりつせいぶんぶんせき、英: independent component analysis、ICA)
信号処理技術の分野で発展した手法で、例えば複数の話者が話した音声データから各話者ごとの音声データを復元する手法です。
独立成分分析を使わないアプローチでも、ガウス性に関する性質からうまく因果の向きを推定することができ、それによって因果グラフを特定します。
LiNGAM
LiNGAMとはLinear Non-Gaussian Acyclic Modelの略で因果探索のセミパラメトリックなアプローチの手法の一つです。LiNGAMの一般的な定式化は以下になります。

xiは観測変数を表しp個あり、eiは外生変数でモデル式で表現されない変動要素を表します。
さて、LiNGAMの仮定をまとめると下記のようになります。
・外生変数と内生変数をつなぐ関数は線形関数とする
・外生変数の分布は非ガウス連続分布とする
・因果グラフは非巡回とする
・(名称には出てこないですが)外生変数は互いに独立とする
これらの仮定からどのようにして因果グラフが導けるかは今回割愛しますが、この辺りの導出過程に興味がある方は参考文献[1]の第4章P87以降をご参照ください。
次に推定時の計算方法について説明します。
推定時の計算方法
LiNGAMの因果グラフ推定には上記で触れた独立成分分析を用いるアプローチと、LiNGAM特有の方法として回帰分析と独立性評価によるアプローチがあります。
- 独立成分分析によるアプローチ(ICA-LiNGAM)
ICA-LiNGAMに関しては、計算過程がそんなに複雑でなくQiitaにも一通りの解説がある(参考文献[11]参照)点や、次回のBMLiNGAMとの関連も考慮して割愛します。
- 回帰分析と独立性評価によるアプローチ(Direct-LiNGAM)
こちらのアプローチでは、観測変数群から2変数を取り出し因果の始まりとなる変数を探す・その変数の影響を取り除いて残りの変数の中でまた因果の始まりとなる変数を探す・・・という作業を繰り返すことで因果グラフを復元します。
2変数の場合
例えば、観測変数群から2変数x1,x2を取り出し、以下の構造方程式モデルが背後にあるものと想定します。

ここでe1,e2は互いに独立かつ非ガウス分布に従い、b21≠0とします。これについて単回帰分析を行い因果順序を推定します。
まずx2を目的変数、x1を説明変数として回帰する場合を考えます。この場合元の構造方程式モデルの第二式がそのまま成り立ちます。そのため、回帰残差はe2となりこれはx1=e1と独立になります。
一方、x1を目的変数、x2を説明変数とした場合、詳細は割愛しますが、回帰残差は

となりe2の項が出てきます。一方冒頭の構造方程式に戻ると、x2は式としてe2を含みますので、この回帰残差と説明変数x2とは従属します。(実はこの従属性の成立には非ガウス分布の仮定を用いていて、具体的にはダルモア・スキットビッチの定理というものを使いますが、ここでは定理の主張だけ書いて詳細は割愛します。興味がある方は参考文献[1]のP114,115をご参照ください。)
・ダルモア・スキットビッチの定理
2つの確率変数y1,y2が、互いに独立な確率変数si(i=1,...,q)の線形和で下記のように表されているとする。この時、もしy1,y2が独立なら、αjβj≠0となるような変数sjはガウス分布に従う。

上記の考察から、両方のパターンで回帰分析を行い残差と説明変数の独立性を判定することで因果の向きを推定することが可能となります。なお独立性の評価には相互情報量という量を用います。(ここでは式は割愛します。)この量が0となるときに独立であると判定しますが、実際には推定誤差があり正確には0にはならないため、相互情報量が0に近い方を独立とみなして因果の順序を決めます。これ以上の詳細は参考文献[1]のP115以降をご参照ください。
3変数以上の場合
上記の例を基に3変数以上の場合の因果グラフの復元手順は下記のようになります。
1. 観測変数群から因果の大元になる変数を見つける。
1-1. 観測変数群から2変数を取り出し単回帰分析を行い残差と説明変数の独立性分析を行う。
1-2. 全ての観測変数の中で最も多く因果の始まりと推定された変数を大元の変数とする。
2. 大元の変数の寄与を他の変数から取り除いたうえで、次の大元の変数を見つける。
2-1. 大元の変数を説明変数、残りの各変数を目的変数とした線形回帰を行い残りの各変数ごとの回帰残差を求める。
(詳細は割愛しますが冒頭のLiNGAMの式で述べたek(ただしkは因果の大元の変数の添え字)がこれらの回帰残差の成分には出てこなくなります。)
2-2. 独立性分析により最も多く因果の始まりと推定された変数を、次の大元の変数とする。
3. 次の大元の変数の寄与を他の回帰残差から取り除たうえで、更に次の大元の変数を見つける。
3-1. 次の大本の変数を説明変数、大元の変数の回帰残差を目的変数とした線形回帰を行う。
3-2. 独立性分析により最も多く因果の始まりと推定された変数を、更に次の大元の変数とする
4. 手順3. を繰り返して因果の順序を推定し観測変数の因果グラフを抽出する。
Google Colabでの実装
ここでは上記で紹介したLiNGAMをGoogle Colabを使って動かすチュートリアルを紹介したいと思います。
Google Colabとは
Google ColabとはGoogleが開発したJupyter形式で使えるクラウド実行環境のことです。Googleアカウントがあればだれでも基本的には無料で使えるので、まだ使ったことのない方は今回のような機械学習の実行テスト等に活用してみてください。
以下、
の実装に、コメントで解説を入れながらGoogle Colabで実行してみます。
準備
# Google Colabにlingamのライブラリをインストールする
!pip install lingam
# lingamと合わせて分析に必要なライブラリをインポートする
import numpy as np
import pandas as pd
import graphviz
import lingam
from lingam.utils import make_dot
# ライブラリのバージョンを表示する。
print([np.__version__, pd.__version__, graphviz.__version__, lingam.__version__])
# numpyでの小数点以下桁数表示と指数表記の禁止を設定する。
np.set_printoptions(precision=3, suppress=True)
# 再現性のためにランダムシードを固定する。
np.random.seed(0)テストデータ作成
元のnotebookでは一様分布ですが同じにしても芸がないので、今回ジップ分布にしてみます。ジップ分布については参考文献[12] を参照いただきたいのですが、ウェブページへのアクセス頻度等で出てくる分布のようです。
a=2 # zipf関数で使うパラメータです。とりあえず2としておく
x3 = np.random.zipf(a, 1000)
x0 = 3.0*x3 + np.random.zipf(a, 1000)
x2 = 6.0*x3 + np.random.zipf(a, 1000)
x1 = 3.0*x0 + 2.0*x2 + np.random.zipf(a, 1000)
x5 = 4.0*x0 + np.random.zipf(a, 1000)
x4 = 8.0*x0 - 1.0*x2 + np.random.zipf(a, 1000)
X = pd.DataFrame(np.array([x0, x1, x2, x3, x4, x5]).T, columns=['x0', 'x1', 'x2', 'x3', 'x4', 'x5'])
import matplotlib.pyplot as plt
plt.hist(x3, bins=20)
再現する因果グラフの確認
# グラフ構造を表す隣接行列を表示する
m = np.array([[0.0, 0.0, 0.0, 3.0, 0.0, 0.0],
[3.0, 0.0, 2.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 6.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[8.0, 0.0,-1.0, 0.0, 0.0, 0.0],
[4.0, 0.0, 0.0, 0.0, 0.0, 0.0]])
dot = make_dot(m)
# Save pdf
dot.render('dag')
# Save png
dot.format = 'png'
dot.render('dag')
dot
因果探索実行
# インスタンスを生成して、.fitするだけで簡単に実行できる
model = lingam.DirectLiNGAM()
model.fit(X)ここで、lingam.DirectLiNGAMのパラメータについて少し補足します。Direct-LiNGAMの実装によると、random_state, prior_knowledge, measureが設定できます。randam_stateは割愛してそれ以外のパラメータについて説明します。
・prior_knowledge
このパラメータはデータの因果構造に関する事前知識をLiNGAM実行時に反映させるためのものです。観測変数×観測変数の二次元array形式で渡すデータで、下記の定義に沿って中身の値を決めます。
(i,j)成分が0・・・xiからxjへの因果が無いことを表します。
(i,j)成分が1・・・xiからxjへの因果があることを表します。
(i,j)成分が−1・・・xiからxjへの因果が不明であることを表します。
・measure
このパラメータは因果順序を判定するときにkernel法を使うかどうかを決めるもので、pwling, kernelのどちらかを選べます。指定しなかった場合はpwlingとなります。基本的には特に指定しなくて大丈夫ですが、仕組みが気になる方はpwlingに関しては
及び参考文献[1]のP119が参考になります。
結果表示
# LiNGAMで推定された因果グラフを表す隣接行列を表示する
# (i,j)成分の中身の値はx_iからx_jへの因果係数b_ijを表す
model.adjacency_matrix_array([[0. , 0. , 0. , 3.023, 0. , 0. ],
[2.98 , 0. , 1.96 , 0.265, 0. , 0. ],
[0. , 0. , 0. , 5.979, 0. , 0. ],
[0. , 0. , 0. , 0. , 0. , 0. ],
[6.067, 0. , 0. , 0. , 0. , 0. ],
[3.922, 0. , 0. , 0. , 0. , 0. ]]) # 上記の隣接行列から因果グラフを表示する
make_dot(model.adjacency_matrix_)
ぱっと見は異なるグラフに見えますが、
・x2からx4の因果が復元できてない、
・元々なかったx3からx1への因果が出てきている、
・x0からx4への因果効果が若干小さく見積もられている
以外は概ね再現できているようです。
最後に
今回は因果探索のセミパラメトリックなアプローチであるLiNGAM、特にDirect-LiNGAMを扱いました。ただしこの手法では未観測な共通原因がある場合に適切に因果を抽出できないという弱点があります。次回の記事ではこの問題に対応するために通常のLiNGAMを拡張したBMLiNGAM(Bayesian Mixed LiNGAM)という因果探索手法を紹介します。
こちらも合わせてお読みいただければ因果探索についてより理解が深まると思います。是非よろしくお願いします。
参考文献
■因果探索全般
・統計的因果探索(機械学習プロフェッショナルシリーズ)著者:清水昌平
因果推論の基本から丁寧に解説されているので入門に適しています。本記事で割愛した数式部分も丁寧に記述されています。
[1] https://www.kspub.co.jp/book/detail/1529250.html
・構造方程式モデルによる因果推論: 因果構造探索に関する最近の発展
今回話に盛り込めなかった細かいことが色々触れられています。上記と合わせて読むと頭の整理になると思います。
[2] https://www2.slideshare.net/sshimizu2006/bsj2012-tutorial-finalweb
・因果探索入門 滋賀大学e-learning教材
動画で学びたい方やざっくり概要を把握したい方向けにおすすめです。
[3] https://www.youtube.com/watch?v=IfpQdlbskpI&list=PLL4x1Hu-A7jyQvYG3oTidZJJ6-fRF4d4l&index=3
■論文
・ICA-LiNGAM
[4] https://www.cs.helsinki.fi/group/neuroinf/lingam/JMLR06.pdf
・Direct-LiNGAM
こちらはDirect-LiNGAMの論文ですが、P.1228に今回割愛したICA-LiNGAMの計算方法が書いてあります。
[5] https://www.jmlr.org/papers/volume12/shimizu11a/shimizu11a.pdf
■実装
・ライブラリ
色々な機能の使い方や出力結果がNotebook形式で提供されており、実際に使う際には参考になります。
[6] https://lingam.readthedocs.io/en/latest/index.html
・実装サンプル
今回使ったもの以外の色々な使い方がNotebook形式で提供されています。
[7] https://github.com/cdt15/lingam/tree/master/examples
・Direct-LiNGAMの実装例
[8] https://github.com/cdt15/lingam/blob/master/examples/DirectLiNGAM.ipynb
[9] https://github.com/cdt15/lingam/blob/master/examples/DirectLiNGAM(PriorKnowledge).ipynb
[10] https://github.com/cdt15/lingam/blob/master/examples/DirectLiNGAM(Kernel).ipynb
■その他解説
・ICA-LiNGAM
個人の勉強記事ですがICA-LiNGAMについて丁寧に解説されています。
[11] https://qiita.com/k-kotera/items/6d7f5598464e18afaa7c
・ジップの法則
[12] https://ja.wikipedia.org/wiki/%E3%82%B8%E3%83%83%E3%83%97%E3%81%AE%E6%B3%95%E5%89%87
