
非劣性検定を用いたA/Aテストの方法
電通デジタルでデータサイエンティストをしている中嶋です。本記事は電通デジタルアドベントカレンダー2021 14日目の記事になります。
この記事について
この記事では実務におけるA/Aテストがどういうものかを説明し、統計的仮説検定を応用した非劣性検定(non-inferiority test)という手法を用いたA/Aテストのやり方を解説します。予備知識として統計的仮説検定の一般的な考え方、また効果量の概念的な理解を前提としています。もしこれらの内容を知らない場合は以前書いたこちらの記事をご参照ください。
A/Aテストとは
A/Aテストについて説明する前にA/Bテストについて簡単に解説します。
A/Bテスト
無作為化比較試験によって施策の効果を測定する方法です。検証したい集団をランダムに2つのグループ(群)に分けて、片方のテスト群に広告配信などの介入を行い、もう片方の何もしないコントロール群とCVRなどの目標となる成果指標を比較して介入の効果を測定する手法です。

A/Aテストの定義
これに対してA/AテストとはA/Bテストをする前段階で各群が同じ状況になっているかの確認を行うものです。上記のA/Bテストでは最初にランダムに2つの群に分割して同等性を担保していますが、実務においてはランダムに分割していても思わぬ形でバイアスが入ってしまい結果指標に影響を与えてしまうことがあります。これを事前に検証することがA/Aテストの目的です。

A/Aテストが効果を発揮するケース
A/Aテストが効果を発揮するケースとして、下記のような事例があります。
テスト群とコントロール群の抽出比率が偏っているケース
介入実験の後に控える仮説検定においては十分なデータ数があれば平均値を正規分布と仮定してp値を計算することも多いと思いますが、この時に各群の抽出比率が90%/10%等で偏っていると正規分布への収束率に違いが出てきてしまうため、成果指標に差が出てしまうケースがあります。
また、システムがLRU方式のキャッシュの場合、各群でキャッシュエントリーに偏りが生じることで成果指標に差が出てしまうことも考えられます。異なるハードウェアから各群のサンプルを抽出するケース
ハードウェアの違いが各群の成果指標の違いを生むとは、(ハードウェアの仕組みや計算機科学に明るくない筆者一個人の感覚としては)一見考えにくいのですが、Facebookが過去に行ったA/Aテストではこれが原因になっている場合があります。(出典:参考文献[1])出現頻度は低いが結果指標に大きな影響を与える特徴が存在するケース
例えば超高年収かつ超ヘビーユーザーを含む集団から各群をサンプリングし、施策実施後に平均購入金額を比較したいケースなどが考えられます。このような状況では、ランダム分割でテスト群とコントロール群を分けたとしても偶然どちらかの群にその特徴を持ったサンプルが多くなってしまい成果指標に差が出てしまう可能性があります。
いかがでしょうか?ともすると普段はあまり気に留めずにA/Bテストをしてしまうこともあると思いますが、A/Aテストを行わないと意図せずバイアスが生じてしまい気づかないうちに誤った介入効果を結論付けてしまう危険性があります。上記のような例を見ても分かる通り、かなりの注意深さや背景知識がないと事前に気づくのが難しい場合もあるため可能な限りA/Aテストを事前に行うことが推奨されます。 次の節で実際のやり方を見ていきます。
p値の分布を利用したA/Aテストの方法
A/Aテストの具体的な実施方法として、ここでは参考文献[2]で紹介されているp値の分布を検定する方法を紹介します。考え方としては、ランダムに分けた2つの群の間で差がない場合にp値が一様分布に従うことを利用して、p値のサンプルを大量に作り適合度検定にかけることで少なくとも有意差は無いことを検証します。
手順
母集団からテスト群/コントロール群をランダムサンプリングし結果指標を計算する。
二群間で成果指標に関する有意差検定のためのp値を算出する。
手順1. ~2. を1,000回繰り返し、p値を1,000個生成する。
※この繰り返しを行う際は母集団の時点を変えてサンプリングすることで時系列による変化等がないかを考慮することが出来る。同じ指標でのA/Bテストを期間を置いて何度か実施する場合はこのような時点ごとに変えたサンプリングを行うことが推奨される。
※この1,000という数字は、10個の階級の中で最大の比率と最小の比率の差が0.1以上の時に有意水準0.05、検出力0.9を担保するために必要な件数となっている。1,000個のp値を階級幅0.1で10個の階級に分類する。
各階級幅に入るp値の個数を、各階級の確率が1/10の離散一様分布を帰無仮説とした適合度検定にかける。
有意差が出なければ同じように分割した2つの群でA/Bテストを行う。
有意差が出た場合の対応策については割愛します。気になる方は参考文献[2]のP217~218に記載がありますのでそちらをご参照ください。
非劣性検定とは
ここからは上記のA/Aテストを行うためのもう一つの方法として非劣性検定について解説します。そして非劣性検定を組み合わせた同等性検定を使ってA/Aテストを行う方法を紹介します。
非劣性検定の説明に入る前に、統計的仮説検定に関する一般的な注意について補足をします。
帰無仮説に対する誤解
統計的仮説検定の考え方は以前こちらの記事でも述べた通り、帰無仮説を仮定して検定統計量を計算し、その時のp値から対立仮説を支持するかを判断するものです。この時、帰無仮説を棄却しなかった場合はどのように結論付けるべきでしょうか?よくある誤解では帰無仮説が正しいと解釈してしまうことがありますが、帰無仮説が棄却されないからといって帰無仮説が支持されるわけではありません。この場合正しくは帰無仮説が成立するかどうかを結論付けることはできません。
このように通常の仮説検定では差があることを結論付けることはできても、差がないこと=同質であることを結論付けるようには出来ていません。
概要
非劣性検定は元々医療統計の分野で既存薬より副作用の少ないあるいは服用頻度が少なくて済むような新薬の効果が、既存薬と比べて劣っていない(=非劣性)ことを示すために使われていました。非劣性検定では次に説明する非劣性マージンΔという量を導入することで通常の仮説検定の考え方を踏襲しつつも劣っていないこと・差がないことを積極的に示すことができます。
非劣性マージンΔの導入
冒頭の仮説検定に関する補足でも触れた通り、通常の仮説検定では劣っていないこと・差がないことを示すことはできませんが、臨床的に(あるいはビジネス的に)意味のある最小の差Δ(非劣性マージン:non-inferiority margin)を導入することで、仮説検定の形で非劣性すなわち差Δ以上は劣っていないことを検証することができます。このΔという量の決め方については明確なコンセンサスがあるわけではなく、臨床試験では別途用意した効果量を基準として0.2~0.5倍した値が使われることが多いようです。
定式化
非劣性検定で使う各種数値と検定方式を定式化します。なおこれ以降は実務におけるCVRやCTRの検定を想定して、独立な母比率の差の検定に絞って説明します。これ以外の設定での非劣性検定については参考文献[3]をご参照ください。
テスト群、コントロール群の母比率をpA,pBとし、各群のサンプルサイズをnA,nB、出現頻度をrA,rB、また、^pA=rA/nA, ^pB=rB/nBとします。このとき非劣性検定を片側検定
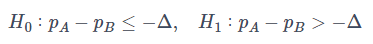
と定式化します。対立仮説のイメージは下記のようになります。

pA−pBが−Δより大きいことがいえると、pAはpBよりも小さくはないことが言えます。厳密にはpA−pBが−Δと0の間の可能性もありこの時には小さいと言えそうですが、Δを意味のある最小の差としていたので、それより絶対値が小さい場合は同じとみなすということです。またあくまで劣っていないことを示すだけなので、可能性としてpAがpBを大きく上回ってしまう(図ではpA−pBがΔよりも更に右側に位置する)こともあり得ます。
検定統計量Z及び片側有意水準 α2 の棄却域は、正規近似を行うことで
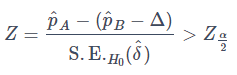
となります。ただし、上式左辺の分母の値は帰無仮説に基づく標準誤差を表し、
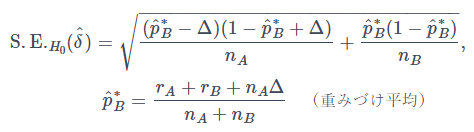
によって計算されます。
ここで ^pB∗ は帰無仮説の下での重みづけ平均を表しますが、元の pA,pB が1に近い場合、この重みづけ平均が1を超えてしまう可能性があります。対策として帰無仮説の下での対数尤度最大化によって算出する方法がありますが、計算が複雑なためここでは割愛します。(詳細が気になる方は参考文献[3]のP138をご参照ください。)
同等性の検定
上記の定式化では検定の結果帰無仮説を棄却しても劣ってないことを示すだけで、同等とまでは言えません。同等性の検定では、上記の非劣性検定を行ったうえで更にAとBを入れ替えて同様の非劣性検定(片側有意水準α2)を行います。
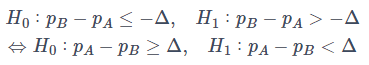
両方で帰無仮説を棄却できると下記のように差の絶対値がΔ以内に収まるので、これをもって同等性を担保します。

ちなみに厳密性には欠けますが、上記の2つの非劣性検定を両方とも棄却することは、pA−pBの信頼区間がすっぽり[−Δ,Δ]の範囲に収まることと近似的には同じになります。ただし、nAとnBの数が大きく異なっていたり、pAとpBがかなり異なる水準の場合はこの近似は正確ではなくなります。
Python実装
ここからは上記の非劣性検定のPythonコードを紹介します。Pythonでは非劣性検定用のライブラリを見つけられなかったため、上記の数式を元に非劣性検定を行う関数を作成します。
# 必要なライブラリのインポート
from scipy.stats import bernoulli
from scipy.stats import norm
import numpy as np
# 実験用データ生成時のランダムシード固定
np.random.seed(seed=123)
# 非劣性検定(独立な母比率の差の検定)の定義
def ratio_non_inferiority_test(A, B, nm_A, nm_B, delta, alpha = 0.05):
'''
A: A群のデータ(list型)
B: B群のデータ(list型)
nm_A: A群の名前
nm_B: B群の名前
delta: 臨床的に(あるいはビジネス的に)意味のある最小の差
alpha: 有意水準
H_0: p_A - p_B <= - delta
H_1: p_A - p_B > - delta
'''
A_size = len(A)
B_size = len(B)
print('{}群の平均:{}'.format(nm_A, np.mean(A)))
print('{}群の平均:{}'.format(nm_B, np.mean(B)))
p_B_hat_star = (sum(A) + sum(B) + B_size*delta)/(A_size + B_size)
SE_h0 = np.sqrt((p_B_hat_star - delta)*(1 - p_B_hat_star + delta)/A_size + p_B_hat_star*(1 - p_B_hat_star)/B_size)
Z = (np.mean(A) - np.mean(B) + delta)/SE_h0
print("Z= {}".format(Z))
if Z >= norm.ppf(1-alpha/2):
print("{}群は{}群よりも発生率で{}以上は劣っていない".format(nm_A, nm_B, delta))
else:
print("帰無仮説は棄却されない")上記の関数を用いて、例えば次のような状況で同等性検定を行うことを考えてみます。
A1群とA2群をランダムに分け、A1群にのみ介入を行いA2群と比較することでCVRの施策介入効果を分析したい。分析にあたっては、事前の検証でサンプリング元の母集団では普段のCVRはおよそ5%であることが分かっている。またビジネス側の担当者に確認して施策効果として0.3%pt以上の差があることが望ましいことが分かっている。
この時に実験的に次の3つのパターンを考え、それぞれで同等性検定の結果がどうなるかを考察します。
A1群とA2群とでCVRが一致している
A1群とA2群とでA1群の方がCVRが0.1%pt大きい
A1群とA2群とでA1群の方がCVRが0.3%pt大きい
最初に各パターンで共通する部分を記述します。
# サンプルサイズを決めるパラメータ
A1_size = 120000
A2_size = 120000
# 臨床的に(あるいはビジネス的に)意味のある最小の差delta(非劣性マージン)を決める
delta = 0.003各パターンごとに0:CV無し、1:CV有りでベルヌーイ分布に従うデータを生成し、非劣性検定を各群入れ替えて2回行うことで同等性検定を行います。まずパターン1の場合を試します。
# パターン1:A1群とA2群とでCVRが一致している
# ベルヌーイ分布のパラメーターを指定
p = 0.05
p_A1 = p
p_A2 = p
# 比率パラメータからベルヌーイ分布を使ってサンプルサイズ分のサンプルを生成
A1 = bernoulli.rvs(p_A1, size=A1_size)
A2 = bernoulli.rvs(p_A2, size=A2_size)
print("---------A1群 vs A2群 の非劣性検定---------")
ratio_non_inferiority_test(A1, A2, 'A1', 'A2', delta, alpha = 0.05)
print("---------A2群 vs A1群 の非劣性検定---------")
ratio_non_inferiority_test(A2, A1, 'A2', 'A1', delta, alpha = 0.05)出力結果
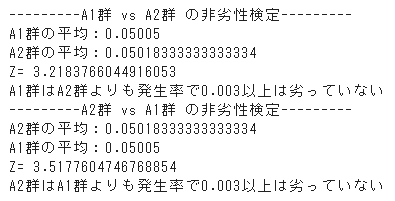
事前のベルヌーイ分布のパラメータが同じなので2回の非劣性検定は両方とも帰無仮説を棄却することができ、同等であることが検証できました。
次にパターン2を試してみます。
# パターン2:A1群とA2群とでA1群の方がCVRが0.1%pt大きい
# ベルヌーイ分布のパラメーターを指定
p = 0.05
p_A1 = p + 0.001
p_A2 = p
# 比率パラメータからベルヌーイ分布を使ってサンプルサイズ分のサンプルを生成
A1 = bernoulli.rvs(p_A1, size=A1_size)
A2 = bernoulli.rvs(p_A2, size=A2_size)
print("---------A1群 vs A2群 の非劣性検定---------")
ratio_non_inferiority_test(A1, A2, 'A1', 'A2', delta, alpha = 0.05)
print("---------A2群 vs A1群 の非劣性検定---------")
ratio_non_inferiority_test(A2, A1, 'A2', 'A1', delta, alpha = 0.05)出力結果

A1群のCVRの方が若干大きく見えますが、事前に設定した非劣性マージン0.003よりも小さいため、パターン1と同じく同等であることが検証できました。
最後にパターン3を試してみます。
python
# パターン3:A1群とA2群とでA1群の方がCVRが0.3%pt大きい
# ベルヌーイ分布のパラメーターを指定
p = 0.05
p_A1 = p + 0.003
p_A2 = p
# 比率パラメータからベルヌーイ分布を使ってサンプルサイズ分のサンプルを生成
A1 = bernoulli.rvs(p_A1, size=A1_size)
A2 = bernoulli.rvs(p_A2, size=A2_size)
print("---------A1群 vs A2群 の非劣性検定---------")
ratio_non_inferiority_test(A1, A2, 'A1', 'A2', delta, alpha = 0.05)
print("---------A2群 vs A1群 の非劣性検定---------")
ratio_non_inferiority_test(A2, A1, 'A2', 'A1', delta, alpha = 0.05)出力結果
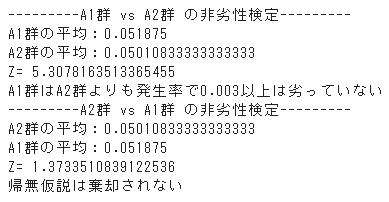
A1群のCVRを非劣性マージン分高く設定しているため二つ目の非劣性検定では棄却できず「A2群はA1群よりも発生率で0.003以上は劣っていない」とは言えないことが分かりました。何度か同様のサンプリングを繰り返しても棄却できないケースが多い場合はサンプリングの仕方にバイアスがないかを確認してみましょう。
最後に
今回の記事ではA/Bテストの前に行うA/Aテストという考え方を紹介しました。巷にあふれるSoTA(State of the Art:機械学習の分野で「最も高精度」なことを指す)を達成した深層学習モデルの話題と比較するとなかなか地味なテーマですが、A/Bテストを用いた因果効果の分析などの場面でより一層の品質を担保する必要がある場合には是非取り入れてほしい考え方となります。
またA/Aテストの実施に当たってp値を検証する方法と非劣性検定を行う方法を紹介しました。非劣性検定は産業界での活用事例はあまり見かけませんが、間違った結論が大きな悪影響を及ぼしかねない医療統計の分野で使われている手法であるため、適切に応用できれば分析結果の品質向上にとても役に立つものだと思います。分野の垣根を越えて活用してみるきっかけとなれば幸いです。
参考文献
[1] Design and Analysis of Benchmarking Experiments for Distributed Internet Services. Eytan Bakshy and Eitan Frachtenberg. 2015. WWW'15
https://dl.acm.org/doi/10.1145/2736277.2741082
分散インターネットサービスにおける適切な実験計画のデザインと分析方法についてFacebookが発表した論文です。
[2] A/Bテスト実践ガイド 真のデータドリブンへ至る信用できる実験とは(著:Ron Kohavi, Diane Tang, Ya Xu 訳:大杉直也 ASCII DWANGO 2021年)
https://www.kadokawa.co.jp/product/302101000901/
主にオンラインシステムから取得したデータを想定したA/Bテストの方法論を様々な観点から網羅的に論じた書籍です。本記事では第19章を参照しており、今回紹介しきれなかったA/Aテストが失敗したときの対応策などが解説されています。
[3] 新版 無作為化比較試験 ―デザインと統計解析―(著:丹後 俊郎 朝倉書店 2018年)
https://www.asakura.co.jp/detail.php?book_code=12881
医学系臨床試験などで使われる統計手法を解説したシリーズの一冊です。出てくる事例は医学系の専門的な話題が多いですが、統計手法の解説は医学知識があまりなくても読み進められます。数式で丁寧に記述されており今回の執筆でも大いに参考になりました。今回割愛した非劣性検定を行う上でのサンプルサイズの設計方法や、連続値を扱う場合・交絡因子を調整する場合など異なる状況下での非劣性検定の手法などが解説されています。
[4]非劣性試験の入門(著:奥村 泰之 2017年)
https://www.slideshare.net/okumurayasuyuki/ss-76150180
臨床疫学研究における報告の質向上のための統計学の研究会 第29回研究集会にて発表された資料です。臨床疫学の文脈ですがこちらも非劣性検定について詳しく解説されています。
