
統計的仮説検定における多重検定の問題とその対処法
この記事について
電通デジタルでデータサイエンティストをしている中嶋です。この記事では統計的仮説検定における多重検定の問題を扱い、その対処法について簡単な手法を紹介します。統計的仮説検定についてある程度知っていることを前提としていますが、もし忘れてしまったり、自信が無い方は前回の記事の復習を先にご覧いただくことをお勧めします。
多重検定とは
多重検定の問題
統計的仮説検定は、予め決めた有意水準に対してデータから算出したp値を用いて大小を評価し、帰無仮説の棄却もしくは採択(保留)を判断する統計的手法です。この時に仮説検定の仕組み上、第1種の過誤が有意水準の確率で発生する可能性があります。言い換えると、本当は有意差が無いはずなのに偶然p値が高くなり帰無仮説が棄却されてしまうことで、検定の結果として有意差ありとなってしまう可能性があるということです。(※1)
※1:普段仮説検定を使う際は確かめようのないところなのですが、有意差があると出た場合、それがまるで「統計学によって保証された間違いのない結果である」と捉えてしまっているかのようなケースもあります。もし有意差ありという結果がビジネス側の知見と異なる・説明できないようなケースでは、なぜそのような有意差が出たのかを検定に使用したデータを可視化したり、その他の特徴量を分析したり、それでも分からなければ検定の過誤の可能性も考慮して再度検定を行ったりすることが望ましいです。
もちろん、正しい実験計画を立ててデータの再収集~再実験~再検定を行うことは相応の時間・費用コストもあるので一概にやるべきというわけではないですが、このような可能性を頭の片隅にでも入れておくことはその後の意思決定において大きな失敗を防ぐことにつながると考えています。
この時、1回だけ検定を行う場合であれば特に問題となることは少ないですが、例えば3つ以上の多群での比較等といった場面で仮説検定を行う場合、その多群から2つの群を抽出して逐一仮説検定を行うと、各検定ごとの有意水準以上に偶然の有意差が出てしまい、偽陽性(本当は有意差が無いにもかかわらず検定結果として有意差が出てしまう)の問題が出てきてしまいます。
具体例
具体的に下記のようなケースにおいては、通常の仮説検定ではなく多重比較検定を考えた方が良いと思います。(※2)
※2:ただし、有意差の誤検出にそれほど大きな損失が発生しえない場合は、分析担当者のコミュニケーション能力や分析結果を受け取る人のリテラシーを考慮して、口頭での補足に留めて良い場合もあると思います。
1. あるユーザー群A,Bの差異を把握するために、両方のユーザー群で取得できているデモグラ属性情報(年齢、年収、性別等)、趣味嗜好情報(スポーツに興味あり/なし等)の平均値や比率の差の検定を各属性・趣味嗜好の項目ごとに行い、有意差が出たものを報告する。
2. 都道府県ごとにユーザーの年収を比較するために、どの都道府県ペアで有意差があったかを逐一 t 検定を行い判断する。
3. 機械学習モデルを実運用に乗せた後、予測に使うデータが学習時のデータから共変量シフト(データドリフト)を起こしているかを調べるために、モデリングに使用した数十個の特徴量それぞれについて学習時のデータと直近の予測用データで比較検定を行う。(※3)
※3:データドリフトについてはこちらの過去記事で解説しています。
これらのケースにおいてはいずれの場合も検定を繰り返し行っており、有意差が出やすくなってしまっています。次の定式化でこの問題を整理します。
問題のからくり
ユーザー群の数を5つとして、各群で得られる比尺度データの平均値の比較のためにt検定を行うケースを考えます。帰無仮説としては
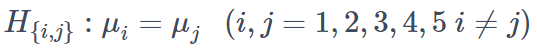
があり、全部で5C2=10個の検定となります。これらに対し対立仮説を
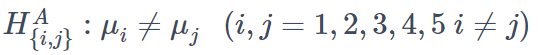
とします。そして各検定における有意水準をα=0.05とします。
この時、各検定個々で考えると有意水準の定義から第一種の過誤は5%です。しかし今回のように複数の検定を同時に行う場合は、第一種の過誤が変わります。第一種の過誤とは、帰無仮説が正しいのに誤って有意差が出てしまう確率のことでした。今回のように複数の検定を同時に行っている場合の全体としての第一種の過誤は、全体で少なくとも一回以上第一種の過誤が起きる確率となります。そのため計算としては全体から一回も第一種の過誤が起きない確率を引くことで
![]()
と求めることができます。
まとめると、個々の仮説検定では有意水準0.05とおいて第一種の過誤がその確率以下になるよう調整して検定していたのにもかかわらず、全体としては40%以上の確率で第一種の過誤が起きてしまう可能性があるということになります。
補足:一元配置分散分析との違い
前述の具体例において特に2. のようなケースでは一元配置分散分析を用いて検定する方法もあるのではないかと疑問に持たれる方もいると思いますので簡単に補足しておきます。
一元配置分散分析では確かに多群での比較検定を行うのですが、この検定の有意差ありの結果は全体としてどこかには差があるとまでしか言えません。具体的にどの群とどの群で有意差があるのか?については一元配置分散分析では分からないのです。
そのため、多群からペアを選んでどの二群で有意差があるのか検定を行いたいわけですが、そのままやると上記の通り第一種の過誤が大きくなりすぎてしまい結果の信頼性を損なってしまいます。
多重比較検定における手法の紹介
上記のような多重比較の問題に対応するための具体的な手法として、ダネットの方法とBH法によるFDR制御について解説します。
ダネットの方法(Dunnett's test)
この手法は多群の比較において、(コントロール群のような)ある特定の群がその他の各群と異なるかどうか、要は1vsその他で仮説検定を行うときに使う手法です。
先述した例とは若干状況が異なりますが、実務上はクリエイティブを変えた複数のテスト群と一つのコントロール群で比較するようなケースで使われることが多いためこちらを採用しました。ちなみに先述のような各ペアでの多重比較に対応する手法としてはテューキーの方法(Tukey's test)というものがあります。
なお、テューキーの方法やダネットの方法では各群の母集団分布は等分散の正規分布を仮定しています。
・考え方
先述した問題において検定全体での第一種の過誤を減らすにはどうしたら良いでしょうか。素朴に考えると個々の検定で使用している有意水準を、よりきつくすれば良さそうです。きつくする方法は色々ありますがダネットの方法ではおおよそ(有意水準)÷(検定の多重数)に調整することで全体での第一種の過誤を小さくします。
今回はこれ以上の詳細な説明は省き実行方法を提示します。具体的な検定統計量の説明等に興味がある方は参考文献[1]をご参照ください。
・実行方法
今回は例として、5つの正規分布に従う群を用意し、うちコントロール群としてN(0,1)、その他のテスト群をN(0,2),N(0,5), N(0.5,2), N(0.5,5)として各群100サンプルを用意します。なお使用言語はRとなります。(Pythonでもstatsmodelsにそれらしい関数はありますがテストしてみたところエラーが取れませんでした。)
set.seed(12345)
a <- rnorm(10, mean = 0.0, sd = 1)
b <- rnorm(50, mean = 0.1, sd = 1)
c <- rnorm(50, mean = 0.5, sd = 1)
d <- rnorm(50, mean = 1.0, sd = 1)
df <- rbind(
data.frame(group = 'A', weight = a),
data.frame(group = 'B', weight = b),
data.frame(group = 'C', weight = c),
data.frame(group = 'D', weight = d)
)
df$group<-as.factor(df$group)
head(df)出力結果(入力データ形式)
下記でダネットの方法を実行できます。コントロール群の指定はカテゴリ名の値が最も小さいもの(今回では"A")が勝手に選ばれるようになっています。
#Dunnett法
library(multcomp)
summary(glht(aov(weight~group, data = df),linfct=mcp(group="Dunnett")))出力結果

出力結果の見方はRでの一般的な検定と同様になっています。今回のデータではA群と比較して平均値に5%有意差があるのは、D群のみとなりました。
BH法によるFDR制御(Benjamini-Hochberg法によるFalse Discovery Rate制御)
BH法は多重比較検定を行う際の偽陽性の問題に着目し、棄却域の下限を調整することでこの偽発見率(False Discovery Rate)をコントロールする方法です。元々は遺伝統計学における塩基配列の統計解析で現れる非常に多数のp値から有意差を判断する方法として知られています。こちらの手法は上記のように検定時に数表を必要とせず検定の種類によらない方法なので、実務では使いやすい方法かもしれません。
・偽陽性の問題:再考
最初にこの手法の元となる偽陽性の問題を具体例を交えて説明します。先ほど説明した第一種の過誤と本質は同じですが、ここでは偽発見率の観点からこの問題を再考します。
例えば100個の仮説検定を行い有意となるものを見つけたい、とします。各検定は有意水準5%かつ検出力80%の検定とします。この時に仮に本当に有意差のあるものが5個あり、それ以外の95個は帰無仮説が正しいとします。そうすると実際の検定を行った時に有意差ありと判定される検定の数の期待値は、

となります。そうすると有意差が出る結果のうち偽陽性の回数の割合(これを偽発見率(False Discovery Rate、FDR)と呼ぶ)は4.75/8.75=0.542と半分以上が偶然の有意差となってしまいます。
・BH法の手順
このような問題の対処法として下記のBH法を用いることで偽発見率(FDR)を調整することができます。
1. 多重検定の個数をNとし、各検定ごとに得られたp値をpiとする。
2. 目標となるFDRをqとする。
3.
![]()
として各p値の棄却域をp∗以下と定める。(ただし p(k) は pi を昇順(小さい順)に並び替えたときの k 番目の p 値である。)
4. この時全体としてFDRはq以下となる。
・証明
上記の手順によりFDRがq以下に抑えられることを示します。
検定の個数をN、そのうち帰無仮説が正であるものをN0(≤N)とします。0以上1以下の任意の値 u に対して、各検定のp値が u を下回る個数を R(u) とし、その中で帰無仮説が正である検定の個数を r(u) とします。
この時、偽発見割合(False Discovery Proposition)をFDP(u)=r(u)/R(u)と表すことができます。ややこしいですがFDPは厳密には確率変数です。FDPの期待値を取ったものがFDRとなっています。
上記のBH法を参考にして、

と定めます。この時、p値がp∗(=p(k∗))以下となる場合を全て棄却するとすると、R(p∗)=k∗となります。これを踏まえて、先ほどのFDPに代入して期待値を取ると、
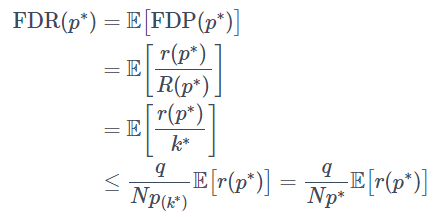
となります。ここで不等式の箇所では k∗ の定義からp(k∗)≤q×(k∗/N) が成立することを用いました。そしてr(p∗)∼B(N0,p∗)となるので(※4)、二項分布の期待値の計算から
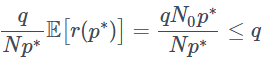
となり、偽発見率がq以下に抑えられることが示せました。
※4:r(u)は帰無仮説が正となるN0個の検定のうちp値がu以下となる個数ですが、帰無仮説が正しいときのp値は一様分布に従い(証明はこちら参照。)一様分布の累積分布の性質からP(p≤u)=uとなるので、u以下となるp値の個数の確率分布は
![]()
となります。
・実行方法
この手法を使うためのPythonライブラリは見つけられませんでしたので、そのまま実装してみます。例として示すだけなので、検定の過程は省略してp値のみが得られている状況で試してみます。
# ライブラリのインストール
import numpy as np
import pandas as pd
np.random.seed(seed=12345)
# 各種数値の設定
N = 100000
alpha = 0.05
beta = 0.1
# 人工データ生成、有意差のないデータは一様分布から生成
insig_ratio = 0.92 # 恣意的
insignificant_size = int(insig_ratio*N)
insignificant = pd.DataFrame(np.random.uniform(0,1,size=insignificant_size))
# 有意差があるデータは検出力0.9となるように有意水準以下となる割合を調整する
significant_1_size = int(np.ceil((1-beta)*(1-insig_ratio)*N))
significant_2_size = int(np.ceil(beta*(1-insig_ratio)*N))
significant_1 = pd.DataFrame(np.random.uniform(0,alpha,size = significant_1_size)).rename(lambda x: x+insignificant_size)
significant_2 = pd.DataFrame(np.random.uniform(alpha,1,size = significant_2_size)).rename(lambda x: x+insignificant_size+significant_1.shape[0])
# データを結合して昇順に整列、indexを保持しておく
p_value = pd.concat([insignificant, significant_1,significant_2]).sort_values(0)
p_value = p_value.reset_index()
# FPRの値を指定する
q = 0.35
# BH法の実行
k_star = max([k for k in range(N) if p_value[0][k] <= q*(k+1)/N])
p_star = p_value[0][k_star]
# 通常の5%有意水準で判定した場合の有意差ありの件数
normal_sig= p_value[p_value[0] <= alpha].shape[0]
# 実際には有意差がない件数 indexを指定することで生成時に有意差なしとしたデータに絞り込む
true_insig = p_value[(p_value[0] <= alpha) & (p_value["index"] < insignificant_size)].shape[0]
print(true_insig,"/",normal_sig,"=",true_insig/normal_sig)4585 / 11605 = 0.3950883239982766
# 参考:上記の期待値は下記で出る。
insig_ratio*alpha/(insig_ratio*alpha + (1-insig_ratio)*(1-beta))0.3963886500429924
# BH法の水準で判定した場合の有意差ありの件数
bh_sig = p_value[ p_value[0] <= p_star].shape[0]
# 実際には有意差がない件数
bh_true_insig = p_value[(p_value[0] <= p_star) & (p_value["index"] < insignificant_size)].shape[0]
print(bh_true_insig,"/",bh_sig,"=",bh_true_insig/bh_sig)13 / 37 = 0.35135135135135137
BH法により、帰無仮説を棄却する数は減ったものの偽発見割合(FDP)を抑えることができました。上記の証明で示したのはあくまで期待値としてなので、実際にはここで見たように予め決めたFDPを超える場合もあります。
最後に
今回は検定の多重性による第一種の過誤の問題について解説し、それに対処する方法として二つの多重比較検定手法を紹介しました。
ダネットの方法は1対多の多重検定において使える方法で、p値を検定の数で補正することでこの問題に対処しています。BH法は偽発見率に着目し指定した偽発見率を下回るようにp値の閾値を調整するものです。
今回扱ったテーマは統計学を学ぶ中ではあまり見かけない話題だと思いますが、第一種の過誤が大きな問題になりうるような検定を行うケース(例えば、有意差ありの対象に対して何かアクションする場合そのコストがとても高くつく場合)で多重比較を行う場合はぜひ試してみてください。
参考文献
・統計的多重比較法の基礎(著:永田 靖・吉田 道弘 サイエンティスト社)
[1]https://scientist-press.com/2019/06/12/igaku-015/
今回のテーマについて、より丁寧な導入から始まり各手法の細かい使い方や具体例まで網羅している本です。詳細について知りたい方はこちらをご参照ください。
・Youtube動画 1.1 多重検定の問題(基本コンセプト)
[2]https://www.youtube.com/watch?v=Mpdlqdnoagw
医療統計の文脈ですが多重検定の問題と各種手法の解説を取り上げています。
・データ科学便覧 Rによるダネット検定
[3]https://data-science.gr.jp/implementation/ist_r_dunnett_test.html
ダネットの多重比較法のR実装が紹介されています。
・データ科学 多重検定 3(著:藤 博幸)
[4]https://sci-tech.ksc.kwansei.ac.jp/~tohhiro/dataScience/dataScience3.pdf
今回扱った偽発見率調整法の詳しい仕組みが解説されています。
・ビジネスデータサイエンスの教科書(著:マット・タディ 翻訳:上杉 隼人、井上 毅郎 すばる舎)
[5]https://www.subarusya.jp/book/b512335.html
本書はビジネスにおけるデータサイエンスの活用法を統計学的な観点から扱った本ですが、本記事で紹介したBH法が紹介されています。本記事にて説明した証明法もこの本を参考にしています。
