統計的仮説検定における効果量の概念と必要サンプルサイズの算出
この記事について
電通デジタルでデータサイエンティストをしている中嶋です。今回の記事では統計的仮説検定における検出力や効果量の概念及び、それらを考慮した事前のサンプルサイズ設計について説明します。読者層としては、既に統計的仮説検定の基本的な使い方を理解している方を主な対象としていますが、そうでない方にもわかるように最初に簡単な復習をします。
統計的仮説検定について
概要
統計的仮説検定(以下、仮説検定)とは、性質の異なるグループ間で平均や分散など各グループを代表するような数値を比較する際に、その差が偶然生じたものか、そうでなく何かしら必然性がありそうかを検証するための統計手法です。例えば比較分析したい2つの群(ex. ユーザーグループ)があった時にある指標(ex. 各群の年齢の平均値)を比較して、統計的に偶然ではないレベルで差異が生じているかを判定したいときに仮説検定を使うことができます。
考え方
仮説検定のアプローチは数学で習う背理法という証明手法に近い考え方をします。背理法とはざっくりいうと、最終的に示したいこと(仮にSと置く)があったときに、その否定(not S)を仮定して論理的な矛盾を導くことです。これにより仮定not Sの正当性が崩れるのでSが支持される、という論法です。
仮説検定においても同様に示したいこと(ex. ある指標が二群間で異なることを示したい)があった時に、その否定(ex. その指標が二群間で等しいということ)を仮定して、矛盾を導きます。示したいことを対立仮説、その否定を帰無仮説と呼びます。
仮説検定では現実のデータを扱うので数学的な意味での厳密な矛盾は示せず、通常は何らかの確率値を計算して「帰無仮説を仮定すると得られる数値が非常に稀なものであるから帰無仮説が適切ではなかったとみなして棄却する」という考え方をします。
実際の判定においてはp値と有意水準という指標を使います。p値とは、帰無仮説を仮定したときに既にあるデータから算出可能な特定の統計量を計算しその統計量が理論上従う分布と照らし合わせて、その値よりも稀な値がでる確率を指します。図で示すと例えば正規分布に従う統計量の値が2.054と出た場合、(両側検定の時)下記の青色の部分の面積がp値となります。
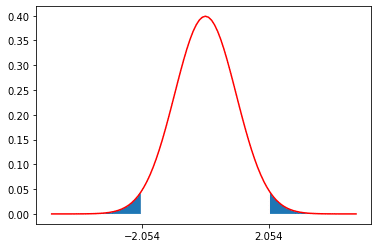
一方、これとは別に予め有意水準という「この値を下回ったら矛盾と言えるくらいに稀な確率」を定めておきます。通常これは5%や1%を使うことが多いです。そして、先ほどのp値と有意水準を比較して、p値が有意水準を下回れば「矛盾と言えるくらい稀な出来事が起きた」として、帰無仮説を棄却し対立仮説を支持します。
説明の都合上p値を先に説明しましたが、実際に検定を行う際は先に有意水準を定めておいてからp値を算出し有意差の判定を行います。
仮説検定に関連する用語
ここからは、実際にサンプルサイズを計算するにあたり必要な概念や指標を紹介します。
検定における二種類の誤り
仮説検定の結果には二種類の誤りがあることが知られています。

・本当は帰無仮説が正しいにも関わらず、検定結果として帰無仮説を棄却して対立仮説が正しいと判定してしまう誤り(第一種の過誤)
・本当は対立仮説が正しいにも関わらず、検定結果として有意差を検出できずに帰無仮説を棄却できない誤り(第二種の過誤)
これらの誤りが発生する確率を通常それぞれ α, βと表記します。
第一種の過誤の確率は有意水準の値と等しくなります。例えば5%有意水準で棄却されるようなp値が得られたときにもちろん帰無仮説が間違っているためにそのような低いp値が得られたという可能性もありますが、一方で帰無仮説が正しくても5%の確率でそのようなp値が出る可能性があり、これが第一種の過誤となります。
検出力(検定力)
上記で説明した第二種の過誤 β に対して、1-βのことを検出力(もしくは検定力)と呼びます。これは対立仮説が正しいときに帰無仮説を棄却する確率となります。
有意水準と検出力はどちらも帰無仮説を棄却する確率を表しますが、それぞれ帰無仮説を仮定したときの棄却確率か対立仮説を仮定したときの棄却確率かで違いがあります。
αとβのそれぞれの特徴及び相互の関係として以下の性質が知られています。
・α は有意水準と等しく、通常は検定を行う分析者が決めることができる。
・β を小さくしようとして棄却域を緩めると、α の値が大きくなってしまう。
・サンプルサイズを大きくすると β を小さくすることができる。
実際に仮説検定を行う際は α の値を予め決めて行いますが、あまり検出力を意識することは無いかもしれません。しかしながら間違いの少ない検定を行うためには検出力も考慮する必要があります。そして実験を行う前にサンプルサイズを算出する時は、予め検出力が満たしてほしい基準を定めたうえで算出します。(このとき上記の3つ目の性質が効いてきます。)
ちなみに事前に決める検定力の基準に関しては特に理論上最適な値というものはなく慣例的に0.8が使われることが多いようです。ちなみにこの数値はCohenによってこちらのP56にて提唱されています。(以下引用)
It is proposed here as a convention that, when the investigator has no other basis for setting the desired power value, the value .80 be used.
(ここでは,分析者が望む検出力を設定するための他の根拠がない場合,値.80を使用することを慣習として提案する。)
効果量
効果量とは、検定を行う際に出てきた差が統計的に有意かとは別に、実質的に意味があるのかを表す指標です。
例えば、ある文房具工場で生産された鉛筆に関して品質検査のために長さが176.0mmと異なるかを検証したいとします。生産した鉛筆からランダムにサンプリングして仮説検定した結果、176.0mmよりも有意に長いことが分かりました。ただ実際のサンプリングした鉛筆の平均長としては176.2mmとなりました。これは実質的にはほぼ同じとみなせそうです。このように有意差は出ているが実質的な違いがあるのかを判定するための一般的な指標として、効果量というものがあります。
・サンプルサイズ設計における効果量の意義
先ほどサンプルサイズ設計においてはα, βを考慮する必要があると書きましたが、実はこの効果量も考慮する必要があります。その効果量の意義について説明します。
仮説検定でのサンプルサイズ設計では、有意水準を決めたうえで上述した検出力を一定以上にするために必要なサンプルサイズを計算します。この時、実際にはほとんど気にならない程度の小さな差にも関わらず検出力を担保しようとする(そのような小さい差でも有意差を検出できるようにする)と、非常に大きなサンプルサイズが必要になってしまいます。こうならないように本質的に意味のある差を設定して、それ以上の差がある場合に高い確率で有意差を検出できる(=検出力を一定以上に保つ)ようにサンプルサイズを設計します。この時の本質的な差として効果量を考える必要があるのです。
・効果量の種類
効果量の概念を提唱したCohenによると、効果量には「グループごとの平均値の差を標準化した効果量」を表すd族と、「変数間の関係の強さを示す効果量」を表すr族の二種類があり、各検定の種別ごとに下記のような種類があります。
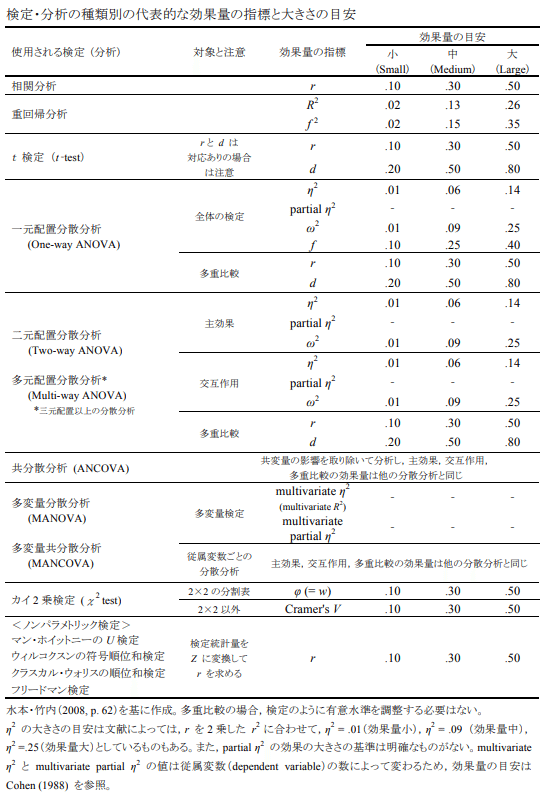
出典:「効果量と検定力分析入門―統計的検定を正しく使うために― 」(外国語教育メディア学会 (LET) 関西支部 メソドロジー研究部会 2010年度報告論集)より抜粋
検定種別ごとの効果量についてその値が大きいのか小さいのか、おおよその目安が提示されています。ただしこの効果量の値はあくまで目安なので、実際に使う場合は基準となる値とそこからどれくらい差があれば効果がありそうかをビジネスサイドの方とすり合わせをしたうえでその差から効果量を算出することが望ましいです。
・事後分析における効果量の考慮
ここまで仮説検定を行う際のサンプルサイズの設計のために効果量を紹介しましたが、実験を行った後の仮説検定結果の分析にも効果量を参考することができます。というよりむしろ、効果量を考慮せずに仮説検定を行った際は、特に有意差が出ているケースではその有意差が本当に意味があるのかを確認するために効果量を見ることが推奨されています。
サンプルサイズの計算方法
上記で紹介した検定における誤り、検出力、効果量を考慮して検定に必要なサンプルサイズを算出します。効果量の種類には上記で列挙したものの他に、平均値の差にはCohen's dやHedges' gというものもありますが、本記事では一例として広告配信におけるCTRの差を検証する状況を想定し、比率の差の効果量として使われるCohen's hを取り上げます。そしてその際に必要なサンプルサイズの計算を説明します。
Cohen's h
効果量の具体例として、二群の比率の差の検定で使われるCohen's hという値を紹介します。二群が従う確率分布をそれぞれX1~B(n1,p1), X2~B(n2,p2)とし、^pi:=Xi/ni (i = 1,2)としたときに、
![]()
と変換します。そしてh = ^φ1 - ^φ2を二群の比率の差の効果量として使います。これがCohen's hの定義です。ただし、この式の三角関数の単位はラジアンです。上記の表の値を使わずに事前に効果量を算出する場合は、社内の過去事例等から適当に当てはめて使います。
なお上記で使った変換は後の数式の導出でも出てきますが、一般的には二項分布の正規近似のための変換の一種で、近似的に
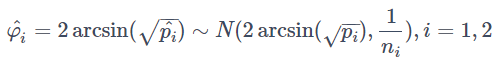
となることが知られています。
状況設定
それでは、ここからは上記のCohen's hを用いて必要なサンプルサイズを計算したいと思います。
例として、ある広告配信キャンペーンで広告クリエイティブを二種類用意しABテストを実施する状況を考えます。具体的には下記の片側検定を行います。
帰無仮説 H0 : test群でのCTR = control群でのCTR
対立仮説 H1 : test群でのCTR > control群でのCTR
この時に、効果量=0.1を有意水準 α=0.05 、検出力 1-β = 0.8 で検定できるようなサンプルサイズ(imp数)を求めることを考えます。ただし簡単のため各群の想定imp数は同じとします。
計算の実行方法
まず先にR(pwrパッケージ)とPython(statsmodelsライブラリ)でのサンプルサイズの算出コードを示します。
# Rコード
# ライブラリの呼び出し
library(pwr)
# pwr.2p.testを使ってサンプルサイズを算出する
# 算出したい数値をNULLにして、それ以外の変数に値を入れる。alternativeは両側/片側検定を指定する。
pwr.2p.test(h = 0.1, n = NULL, sig.level = 0.05, power = 0.8, alternative = "greater")出力結果

# Pythonコード
import statsmodels.stats.power as smp
smp.NormalIndPower().solve_power(effect_size=0.1, alpha=0.05, power=0.8, alternative='larger')出力結果
![]()
結果を見ると、必要なサンプルサイズはtest群、control群それぞれで1,237件あればよいようです。この件数の意味を少し補足すると、test群/control群それぞれで1,237件以上のサンプルが確保されていれば、効果量0.1の差を有意水準0.05、検出力0.8で見つけることができる、ということになります。
計算式の確認
上記のパッケージでは中身の計算が全く分からないので、同じ計算を数式で追ってみます。
結論としては下記の式にそれぞれ代入して、残った変数について解くと必要なサンプルサイズが算出されます。
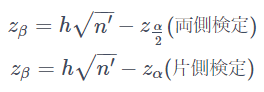
ただし、test群/control群それぞれのサンプルサイズn1,n2に対しn′=n1×n2/(n1+n2)とし、αを有意水準、βを第二種の過誤の確率、hを効果量としています。また、z_γは標準正規分布の上側確率が100γ%となるパーセント点を表しています。上記の例に当てはめてみると、
n1=n2=nとするとn′=n/2、
α=0.05でz_α=z_0.05=1.64485、
β=0.2でz_β=z_0.2=0.84162、
h=0.1なので、
n=2×{(0.84162+1.64485)/0.1}^2=1236.5066
となり、先ほどのR/Pythonの結果を再現することができました。
導出
ここからは先ほどのサンプルサイズの計算式を導出してみようと思います。
まず、検定の概要を整理します。X1 ~ Bi(n1, p1), X2 ~ Bi(n2, p2)$とし、これらは独立とします。この時、片側検定問題は
帰無仮説 H0:p1=p2
(片側)対立仮説 H1:p1>p2
で、^p = (X1+X2)/(n1+n2), ^p1 = X1/n1, ^p2 = X2/n2とすると検定統計量は通常
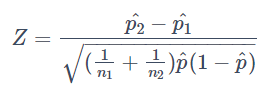
となります。ですが今回の導出ではCohen's hとの整合性を考慮して先ほど出てきた
![]()
の変換を行い、
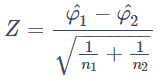
を検定統計量として使います。有意水準αに対する棄却域としてはZ>z_αとなります。この下で検出力の定義からまず
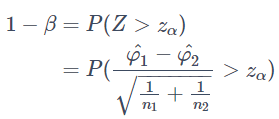
が成り立ちます。ただし、右辺の確率Pは対立仮説を仮定したときの確率です。対立仮説においてはp1−p2>0 で2arcsin(√p1)−2arcsin(√p2) > 0となるので、
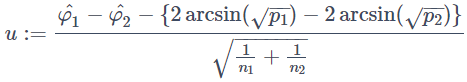
とおくと、u∼N(0,1)となります。これを用いて

となります。ここで最右辺のPの中身の分子の部分をCohen's hとしてhに置き換えてn′=n1×n2/(n1+n2)とおくと
![]()
なります。よって、
![]()
となり冒頭の式が示されます。
最後に
施策の効果検証時に仮説検定を使う方も最近では増えてきている印象ですが、なかなか効果量まで考慮してサンプルサイズ設計を事前に行っている事例は少ないのではないでしょうか?今回紹介したようなweb広告におけるCTRの仮説検定では、サンプルサイズが足りなくなる可能性はあまり無いですが、機会損失をできるだけ減らすためにcontrol群を必要最低数にしたいケースなどでは、今回紹介したようなサンプルサイズ設計をすることで有意水準や検出力といった仮説検定の品質を担保することができます。
また、逆にサンプルサイズが多すぎてしまい、ぱっと見ほとんど意味がないような差にも拘わらず有意差が出てしまうようなケースにおいても、事後的に効果量を見ることで過去施策の効果量と比べながらある程度客観的な議論ができます。
仮説検定の際の差が付くテクニックとして是非身に着けていただければ幸いです。
参考文献
・サンプルサイズ全般の本
サンプルサイズの決め方 永田靖,朝倉書店,2003年
http://www.asakura.co.jp/books/isbn/978-4-254-12665-5/
書名の通りサンプルサイズの決め方について丁寧に説明されています。今回紹介していない仮説検定のサンプルサイズの算出も載っています。
なお、本書では効果量という言葉はほとんど出てきませんが、実際のサンプルサイズの算出において Δ という量を使っておりこれが実質的な効果量の役割を果たしています。
・サンプルサイズの算出式
Tests for Two Proportions using Effect Size(NCSSというサンプルサイズ算出用ソフトウェアのドキュメント)
https://ncss-wpengine.netdna-ssl.com/wp-content/themes/ncss/pdf/Procedures/PASS/Tests_for_Two_Proportions_using_Effect_Size.pdf
Cross Validated How to calculate the power of a test that compares two proportions(海外の機械学習・統計関連の質問サイト)
https://stats.stackexchange.com/questions/258522/how-to-calculate-the-power-of-a-test-that-compares-two-proportions
・効果量の表
外国語教育メディア学会 (LET) 関西支部 メソドロジー研究部会 2010年度報告論集
効果量と検定力分析入門―統計的検定を正しく使うために― 水元篤,竹内理,2010
https://www.mizumot.com/method/mizumoto-takeuchi.pdf
・Rのpwrライブラリに関するドキュメント
https://www.rdocumentation.org/packages/pwr/versions/1.3-0/topics/pwr.2p2n.test
・Cohen's h
Statistical Power Analysis for the Behavioral Sciences Second Edition
Jacob Cohen, LAWRENCE ERLBAUM ASSOCIATES, PUBLISHERS, 1998
http://www.utstat.toronto.edu/~brunner/oldclass/378f16/readings/CohenPower.pdf
こちらの文献のP181の式(6.2.1)、(6.2.2)にてCohen's hの定義が与えられています。
・逆正弦変換
植物防疫 第 56 巻 第 10 号 (2002 年)
正しい分散分析結果を導くための変数変換法 山村光司,2002年
http://jppa.or.jp/archive/pdf/56_10_22.pdf
分散分析文脈での話がメインですが、逆正弦変換についてP438に少しだけ記載があります。
・プールした分散の考察
比率の差Z検定の注意点:統合比率を使う理由
https://biolab.sakura.ne.jp/z-test-proportion.html
