【数学】すぐ分かる集合論入門

1.はじめに

　本記事では、「高校数学でつまずいたけど大学数学を学びたい」、「集合論の概要を理解したい」という方を主な対象として、大学数学の入り口たる集合論の基本事項を解説する。
　解析学、代数学、幾何学、その他応用数学など、その先何をやりたいかというモチベーションは人によって異なるだろうが、モノの集まりとその性質を議論する集合論は全ての数学分野の土台たる位置づけであり、避けては通れない分野である。
　ちなみに、集合論の基本を理解しておけばプログラミングの本も読みやすくなるというメリットもある。
　そして、本記事の位置づけだが、目指すゴールは、文系理系問わず高校1年生ぐらいまでの数学しか覚えていない方でも、現代数学の基本たる集合論の基本概念を理解し、更にその先の分野の教科書を読めるようになることである。
　あくまでも集合論のダイジェストなので、必要に応じて教科書等で補完して頂けたらと思う。

2.集合論入門

2.1 論理と集合

　ここでは、数理論理学における量化子および集合の各種記法について扱う。

定義2.1.1（全称記号と存在記号）
　任意（全て）の$${x}$$に対して、命題$${P(x)}$$が成り立つとき、「$${\forall x P(x)}$$」と書く。
　また、ある$${x}$$が存在して、命題$${P(x)}$$が成り立つとき、「$${\exists x P(x)}$$」と書く。
　尚、全称記号$${\forall}$$、存在記号$${\exists}$$を総称して「量化子(quantifier)」というが、これらは集合論というよりは数学基礎論たる数理論理学（記号論理学）に由来する記法である。

定義2.1.2（集合）
　集合(set)とは「モノ」の集まりのことであり、その集合に属する「モノ」を元または要素(element)という。特に、ある$${a}$$が集合$${A}$$に属しているならば、$${a}$$は集合$${A}$$の元であるといい、$${a \in A}$$で表す。
　尚、集合の記法は2通りあり、$${\{ a,b,c \}}$$のように具体的に集合の元を書き並べてもよいし、命題$${P(x)}$$が真であることを満たすような$${x}$$を全て集めたものという意味で$${\{ x|P(x) \}}$$と書いてもよい。
　また、集合を1つの元とみなし、集合そのものを集めたもの（集合の集合）を集合族(familiy of sets)という。

例2.1.3（集合）
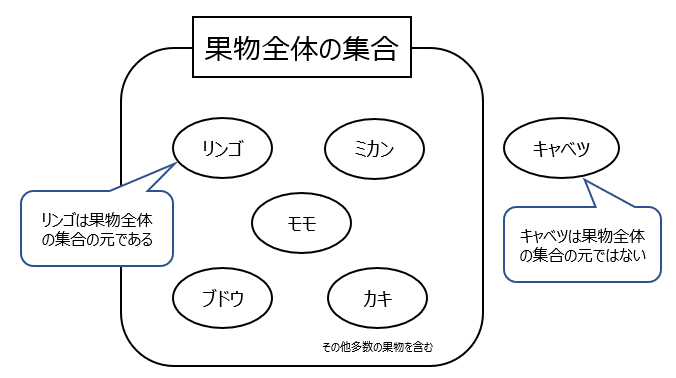
　リンゴを$${f_1}$$、果物全体の集合を$${F}$$としたとき、リンゴは果物全体の集合の元である(リンゴは果物に属する)から、$${f_1 \in F}$$で表すことができる。　
　一方で、キャベツを$${f_2}$$としたとき、キャベツは果物全体の集合の元ではないため、この場合は$${f_2 \notin F}$$で表す。

図1. 集合の例

定義2.1.4（部分集合）
　ある集合$${A}$$に対して、$${A}$$の一部の元から構成される$${B}$$が存在するとき、集合$${B}$$は集合$${A}$$の部分集合(subset)であるといい、$${B \subset A}$$で表す。

例2.1.5（部分集合）
　果物全体の集合$${F}$$から、リンゴとミカンだけを取り出して新しい集合$${S=\{ リンゴ, ミカン \}}$$を定義したとき、集合$${S}$$は集合$${F}$$の部分集合であり、$${S \subset F}$$で表すことができる。

図2. 部分集合の例

定義2.1.6（空集合）
　元が1つも無いような集合を空集合(empty set)といい、$${\emptyset}$$で表す。

定義2.1.7（和集合）
　2つの集合$${A}$$、$${B}$$に対して、少なくとも$${A}$$か$${B}$$のいずれか一方に属する元全体の集合を$${A}$$と$${B}$$の和集合(union)といい、$${A \cup B}$$で表す。

定義2.1.8（積集合）
　2つの集合$${A}$$、$${B}$$に対して、$${A}$$と$${B}$$の両方に属する元全体の集合を$${A}$$と$${B}$$の積集合または共通部分(intersection)といい、$${A \cap B}$$で表す。

例2.1.9（積集合）
　2つの集合$${A=\{ 1,3 \}}$$と$${B=\{ 2,4 \}}$$には、両方に属する元が存在しない。すなわち、$${A \cap B = \emptyset}$$である。

定義2.1.10（直積集合）
　2つの集合$${A}$$、$${B}$$に対して、任意の元$${a \in A}$$と$${b \in B}$$の全ての順序対（順番に意味がある対）$${(a,b)}$$を集めた集合$${\{ (a,b)|a \in Aかつ b \in B \} }$$を$${A}$$と$${B}$$の直積集合(direct product)といい、$${A×B}$$で表す。尚、$${×}$$は「クロス」と読む。

例2.1.11（直積集合）
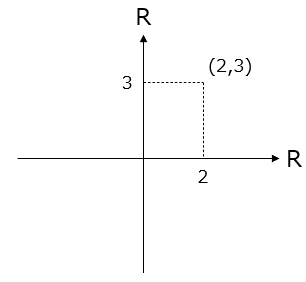
　横軸と縦軸から成る座標があり、それぞれの軸は実数の集合$${R}$$上の値をとるならば、座標上の点$${(x,y)}$$は直積集合$${R×R}$$の元である。
　例えば、座標上のある点(2,3)は、横軸$${R}$$から2をとり、縦軸$${R}$$から3をとってきた順序対であり、この点は座標を表す直積集合$${R×R}$$の1つの元であるといえる。
　また、$${d}$$次元の$${R}$$の直積集合$${R×R× \cdots ×R}$$を考えるとき、$${R^d}$$と表す場合もある。
　さらに、直積集合$${S_1×S_2× \cdots ×S_n}$$であれば$${\prod_{i=1}^{n}S_i}$$という記法もある。

図3. 直積集合の例

2.2 写像

　例えば、関数$${y=2x+4}$$について、$${x}$$の値を入力すれば、$${y}$$の値が一意に定まる。このように、関数とは入力$${x}$$に対応する出力$${y}$$を定めるシステムだと考えてよい。
　そして、この関数という概念を集合論の文脈で一般化したものが写像である。

定義2.2.1（写像）
　集合$${X}$$の元を定めたとき、集合$${Y}$$の元が定まるような操作$${f}$$を$${X}$$から$${Y}$$への写像(mapping)といい、$${f:X→Y}$$で表す。
　また、元$${x \in X}$$に対応する元$${y \in Y}$$を、写像$${f}$$による$${x}$$の像といい、$${y=f(x)}$$で表す。

定義2.2.2（全射）
　写像$${f:X→Y}$$が与えられたとき、任意の$${y \in Y}$$に対して、$${y=f(x)}$$を満たすような$${x \in X}$$が存在するとき、$${f}$$は全射(surjection)であるという。

定義2.2.3（単射）
　写像$${f:X→Y}$$を定めたとき、任意の$${x_i,x_j \in X(x_i≠x_j)}$$に対して、$${f(x_i)≠f(x_j)}$$であるとき、$${f}$$は単射(injection)であるという。

定義2.2.4（全単射）
　写像$${f}$$が全射かつ単射であるとき、$${f}$$は全単射(bijection)であるという。

2.3 濃度

定義2.3.1（濃度）
　ある集合$${A}$$に属する元の個数を$${A}$$の濃度(cardinality)といい、$${|A|}$$または$${#}$$$${A}$$で表す。尚、ここでの$${|・|}$$は絶対値の記号とは無関係で、あくまでも集合論上の記法として用いている。
　また、空集合を含め、濃度が有限であるような集合を有限集合といい、有限集合でない集合を無限集合という。

例2.3.2（濃度）
　ある集合$${A=\{ 1,2,3,4,5,6 \}}$$が与えられたとき、集合$${A}$$の元の個数は6個であるから、$${|A|=6}$$である。

定義2.3.3（可算濃度と連続体濃度）
　自然数全体の集合$${N}$$と濃度が等しい集合を可算集合といい、その濃度を可算濃度という。
　また、実数全体の集合の濃度を連続体濃度という。
　慣例的に、可算濃度を$${\aleph_0}$$（アレフゼロ）、連続体濃度を$${\aleph}$$（アレフ）で表す。

定理2.3.4（ベルンシュタインの定理）
　2つの集合$${A}$$、$${B}$$に対して、$${A}$$から$${B}$$への単射と$${B}$$から$${A}$$の単射が存在するならば、$${|A|=|B|}$$が成り立つ。
　尚、この定理は、集合間の濃度を比較する際に有用となる。

2.4 二項関係

定義2.4.1（関係）
　ある$${x}$$と$${y}$$に何らかの関係(relation)があるとき、$${xRy}$$と書く。関係は、$${=}$$や$${\subset}$$、$${<}$$などを一般化した概念である。

定義2.4.2（反射性、対称性、推移性）
　ある$${A}$$に対して、$${a,b,c \in A}$$とする。
(1) 反射性(reflexive)：$${aRa}$$である。
(2) 対称性(symmetric)：$${aRb}$$ならば、$${bRa}$$である。
(3) 推移性(transitive)：$${aRb}$$かつ$${bRc}$$ならば、$${aRc}$$である。

定義2.4.3（二項関係）
　集合$${A}$$に対して、直積集合$${A×A}$$の部分集合を二項関係(binary relation)という。つまり、集合$${A}$$と集合$${A}$$から元を1つずつ取ってきた順序対の集合のことをいう。

定義2.4.4（同値関係）
　反射性、対称性、推移性を満たすような二項関係を同値関係(equivalence relation)という。

定義2.4.5（順序関係と順序集合）
　$${M×M}$$の部分集合$${\sqsubseteq}$$が反射的かつ対称的かつ推移的ならば、$${\sqsubseteq}$$を順序関係、$${(M;\sqsubseteq)}$$を順序集合(ordered set)という。

2.5 選択公理

　集合論における有名な問題の1つとして、選択公理がある。

定理2.5.1（選択公理）
　空集合を含まないような集合から成る集合族に対して、それぞれの集合から1つずつ元を取り出して新しい集合を構成することができる。これを選択公理(axiom of choice)という。
　詳しくは触れないが、同値な命題として、任意の線形順序部分集合が上限を有する順序集合には、極大元が存在するというZornの補題(Zorn's lemma)もある。

3.集合論の次に何を学ぶか？

　数学科で扱われるような純粋数学を深く学びたいのであれば、通常、集合論の次は位相空間論を学び、そこから更に解析、代数、幾何の諸分野に進んでいくことになる。ちなみに位相空間論については、「集合と位相」のように、集合論とセットで書かれた教科書も多い。
　ただ、本記事の読者は純粋数学をモチベーションにしている方ばかりではないであろうから、工学系向けの微分積分・線型代数の教科書に進むのもよいし、他にもゲーム理論のような経済学、あるいはグラフ理論やオートマトン理論といった離散数学など、集合論のベースを分かっていればある程度着手できるような分野に進むのもよい。
　尚、集合と位相の教科書についていえば、以下に示す参考文献[1]は初学者でも読みやすいと思うので、独習したい方にお勧めである。

参考文献

[1] 内田伏一, 位相入門, 裳華房(2015).
[2] 浪川幸彦ほか, 数学辞典, 共立出版(2017).