Andrew先生の分かりやすすぎるMachine Learning パート② (ともし)
どうも、おしとやか関西人のともしです〜パート1の続きです!
コスト関数が分かったとして、じゃあどうやってコストの最小値を見つけ出すんや?という問いに答えていきたいと思います〜
コストの最小値を見つけ出す2つの方法
1. 最急降下法(Gradient Descent)
2. 正規方程式(Normal Equation)
今回は1の最急降下法についてお話ししていきたいと思います!
微分のおさらい
この最急降下法では微分の考え方を用います。微分についてサクッとおさらいしてみます。
![]()

について考えます。
![]()
微分するとこうなります。
これはどういうことかというと、グラフの各点における傾きを表しています。
例えば
・x = 0の時、2x = 0 なので、
f(x)のグラフはx = 0の時(つまり点(0, 0)の時)、接線の傾きは「0」です。
同様に
・x = 0.5の時、 2x = 1なので、
f(x)のグラフはx = 0.5の時(つまり点(0.5, 0.25)の時)、接線の傾きは「1」です。
グラフ上のある点(p, q)の接線の傾きは、
グラフの方程式を微分したものにおいて、xにpを代入して得られる値になります。
そしてこの仕組みは、「出力yに対して変数がxの1つのみである2次元のグラフ」だけでなく、今回のような「出力Jに対して変数がθ0, θ1の2つ存在する3次元のグラフ」や、高次元においても成り立ちます。
最急降下法
ゴール: 下のコストのグラフから、コストが最小となるような(つまりグラフの最下点における)θ0, θ1の値
最急降下法のイメージは、「山のある地点から、とにかく下を目指して歩いていく」という状態です。

さて、微分の前提知識を頭に最急降下法について考えます。
まず初めにランダムなθ0, θ1を選びます。それが、図の赤い部分にある左端のバツだったとします。この時、先程のお話のように微分を行うことで、この点における接線の傾きの値が得られます。つまり、山の傾きですね。この値/傾きは、微分の仕組み上、θo(もしくはθ1)がほんの少しだけ「増えた」時(つまりあなたが前に進んだ時)にどのくらいJが動くか(どのくらい上に行くのか下に行くのか)、という意味なので、微分値が正であれば、前に進むとJは増えるぞ(山を登ることになるぞ)ということです。前に進めば、θ(その地点の座標)は大きくなります。こうして山を下るための一歩一歩を数式にしたのが、以下になります。

今回はθ0とθ1のふたつなので、この計算をj = 0, 1それぞれの場合で計算します。この値がある値に収束すればそこで終了です。
端的に言えば、θjに「上の式の-αから右端まで」の変化を加えて、θjを更新しています。山の例で言うと、地点θjから、「上の式の-αから右端まで」分だけ進んで、自分の現在地θjを更新するということです。ちなみにその変化は、J方向の高さの変化ではなく、水平方向の変化であることに注意です。
変化分のうち、αの右の塊は、コスト関数J(θ0, θ1)を微分したものです。つまり、(θ0, θ1)地点における、目の前の山の傾きです。正であればあなたは登る向きに立っていて、負であれば下る向きに立っています。我々は最下点を目指しているので下りたいわけです。
αは、learning rate(学習率)です。要は、あなたの一歩の幅で、正の値です。
よって微分値が正であれば、現在地θjから下に進むために後ろに進まないといけない、つまりθを減らさないといけないので、-がαの前に付き、逆に微分値が負であれば、そのまま前に下ればよいのでθjを増やすためには、やっぱり-が必要です(微分値が負なのでθjを増やすためには相殺しないといけない)。


先程の坂を下る公式に、前回のコスト関数の公式をぶちこむと
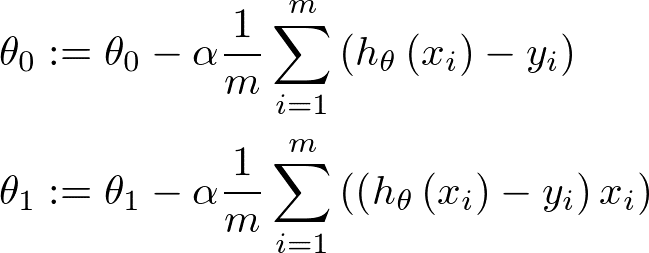
こちらが得られます。若干異なるのは、もちろん微分のせいです。これをコーディングすれば、簡単な機械学習が完成となります。
補足: 学習率αについて
αは一歩の大きさだと述べました。そのαは我々人間が任意に設定することができます。
(i) αが小さすぎる時

一歩一歩が非常に小さいので、解を得るまでに非常に時間がかかってしまいます。
(ii) αが大きすぎる時

αが大きすぎると谷を這い上がるような形で、下から上にどんどん登ってしまい、収束するどころか発散してしまいます。
このようにαは大きすぎても小さすぎてもダメで、うまい具合のαを選ぶことが重要となります。
この記事が気に入ったらサポートをしてみませんか?
