【微積分】 〈３〉 接線（共有点）

　数学の歴史上、「三角比」「図形の性質」などは紀元前から使われていま
すが、「微積分」は、比較的最近の技法のようです。たいへんスマートで、体系的に確立されており、代数と幾何の一対一対応の美しさを味わうことのできる分野です。

---

[Method] 曲線上の点（接点）からの接線

　【微積分】〈２〉 では、接点が与えられ、そこで接する接線を求めました。

接線と曲線の共有点について考えてみましょう。
接している接点は、もちろん共有点ですよね。２次関数では、接点以外の交点はありません。ですが、３次関数では、多くの場合、もう１点共有点（交点）を持ちます。

〈例題１〉

〈例題解答例１〉

[Method] 交点・共有点→連立方程式

　「共有点を求めよ。」は、「連立方程式を解け。」と言っているのと同じ！
（ただし、図で分かれば、その方が最速！）

　例題の解法の中で、３次方程式を解く場面が出てきますが、因数定理を使った因数分解に手こずりそうですが、実は、ここにもMethodがあります！　接点で接しているのですから、接点に対応する解は重解となります。
　つまり、接点の x座標が必ず重解なので、因数定理を使わず、（xーa）^2 が因数なので、３次方程式の定数項をみれば、大まかな因数分解の姿が推測できます。
　例えば、例題では、（x＋１）^2 が因数なので、その定数項は１。３次方程式の定数項は−４なので、（x−４）が残りの因数と推測できるのです。

[Method] 

　接点の x座標が、重解！
　因数定理を使わずに因数分解して、スピードアップ！

---

　実は、３次関数のグラフと直線で囲まれた部分の面積は、３次関数の３次の係数を a とすると、以下で求めることができます。

[Method] 1/12公式

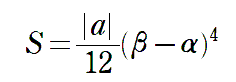
　このこともあって、出題頻度が高いのかもしれません。微分、接線、積分、面積が一連の学習内容が一問で問えるからです。

接点が３重解

　最後に、接点以外の交点がない場合というのは、接点が３重解のになるときです。接していると言えるのか、、、、グラフを見て貰えばわかりますが、交わっているようにしか見えません、、、、が、一応、接しているのです。（微分係数と直線の傾きが一致しているから）
　でも、、、、、どう見ても一般的な接線の概念とは異なってクロスして見えますよね。

---

〈問題２〉

〈問題解答例２〉