ベクトルと中学数学②

ようこそ、クリハロ教室へ
僕はDiscordというSNS上でクリハロ教室の講師をしています。今回は前回から引き続き、高校受験問題を楽して解くべく、Discordの方ではあまり触れない予定のベクトルを学んでいこうと思います。今回は後半戦です。前回の ベクトルと中学数学① をまだご覧でない方は先にそちらを読んでくださると嬉しいです。
(僕のTwitterまでDMを頂けると、クリハロ教室に参加できます。興味の湧いた方は是非！)

そして、あけましておめでとうございます。これが新年一発目の記事になります。より良い2021年にするためにも数学を楽しんでいきましょう！今年もよろしくお願いします。

この記事ではベクトルの上付き矢印を表せないので、ベクトルABやベクトルaは(AB),aと表します。ご了承ください。

＊ 内積の意味を考える

前回の記事のラストで突然出て来た内積
各成分の積の総和にどんな意味があるのでしょうか？結論から言うと、射影です。

ゴルフゲームをプレイしたことはありますか？
風向が矢印で示されたりしていることがあると思います。なんだか風向という向きと風速という大きさを持っていて、ベクトルっぽいですよね。追い風や向かい風なら、飛距離が変わる程度ですが、左右の風は流されてしまって危険です。
ですから、横向きにどれだけ流れるのかを知りたいですが、斜めに吹いたりしていると、結局真右、真左の風向のときと比べて、どれくらい流れるのかよく分かりませんから、困ってしまいます。

そこでこのように、斜めのbという風向と風速でどの程度aの向きに流されるかを考えることができます。
上から光を当てて、aにできた影の部分cの長さということですね。

aとbの内積はこのaとcの大きさ同士の積を表しています。

それでは本当にそれが各成分の積の総和と等しいのか、証明してみましょう。

a₁,a₂,b₁,b₂を用いて、c₁とc₂を表すことを考えてみましょう。
まずaを含む直線の方程式は
y=(a₂/a₁)x …①
またbを含む直線の方程式は
y=(b₂/b₁)x …②

破線を含む直線は(b₁,b₂)を通り(y-b₂=m(x-b₁))
①に直交する(傾きが①の傾きと掛けて-1)
y=-(a₁/a₂)x+(a₁b₁/a₂)+(a₂b₂/a₂) …③

①と③を連立させて、c₁,c₂を求める

(手書きですみません)
こうして、地道に計算すると|a|と|c|の積が前回示した内積と一致していることが分かりますね。特にaを正規化した場合、内積は射影cの長さになります。

垂直だと、この射影の長さが０になるので、零ベクトルでないa,bの内積が０であれば、aとbは垂直と言えたわけです。

ちなみに、大きさ同士の積なので正にしかならないようにも感じますがaとbのなす角が90°を超えて逆側に射影ができる時は負の値になると定義されます。

例えば(0,1)と(1,-2)の内積は-2になります。
このように内積は負の値も取るので注意してください。

＊ 三角関数を使う方法

射影のベクトルcはaとbがなす角θを用いてもっと簡単に表すことができます。その道具が三角関数です。これも高校範囲ですが、今回用いるのは、かなり簡単な部分なので、ベクトルを学ぶのに必要なところだけ少し解説します。

直角三角形において、直角以外の他の一つの角がθと与えられれば、ただ一つの相似形に定まるので(a/c)や(b/c)などはθの関数になります。これを三角関数といいます。

sin(正弦)=対辺/斜辺
cos(余弦)=隣辺/斜辺
tan(正接)=対辺/隣辺

今回はsin,cosの意味とsin²θ+cos²θ=1を覚えておいてくだされば十分です。
先程の内積も三角関数を使うと、図形的に分かりやすく定義できます。
aとbのなす角をθとして、射影の長さを|c|とすると、cosθ=|c|/|b|です。
つまり、|c|=|b|cosθ と示せます。

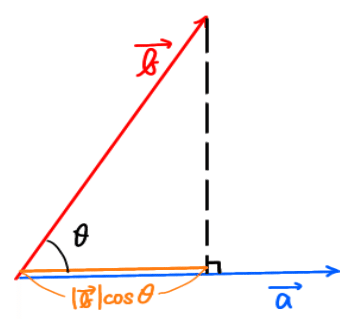
よって、内積はこのように与えられます。

a・b=|a||b|cosθ

これは　a・b=a₁b₁+a₂b₂　の定義と同値です。どちらの定義でも　a・b=b・a　が分かりますね。
|ka|=k|a|から　ka・b=k(a・b)=a・kb
また　cosθ=(a・b)/|a||b|　も言えます。

【面積】

aとbが張る平行四辺形(三角形ならこの半分)の面積は　|a||b|sinθ　になります。

これを式変形してみましょう。

【練習】

A(-3,2),B(2,6),C(4,-2)の３点を頂点とする三角形の面積を求めよう。

(AB)=(5,4) (AC)=(7,-4)
面積は　|-20-28|/2=24

簡単すぎてこれは驚きですね！

＊ ベクトルと空間図形

空間におけるベクトルも成分が３つになるくらいで計算の方法はそこまで変わりません。

a=(a₁,a₂,a₃) , b=(b₁,b₂,b₃) として
ka=(ka₁,ka₂,ka₃)
a+b=(a₁+b₁,a₂+b₂,a₃+b₃)
|a|=√(a₁²+a₂²+a₃²)
a・b=a₁b₁+a₂b₂+a₃b₃=|a||b|cosθ

と、本当に成分が３つになっただけという感じですね。ノルムに関して、しっかりこの定義で大きさになっていることは各自調べてください。

空間においても、平行四辺形の面積を考えてみましょう。√{(|a||b|)²-(a・b)²}とするところまでは、同じ式変形です。これを成分表示に変えてみましょう。

展開して因数分解するのはかなり煩雑なので、省略しましたが、このようにまとめることができます。出て来た式を見てみると
(a₂b₃-a₃b₂ , a₃b₁-a₁b₃ , a₁b₂-a₂b₁)というベクトルのノルムになっていることが分かります。このベクトルをaとbの外積といい、a×bで表します。

a×b=(a₂b₃-a₃b₂ , a₃b₁-a₁b₃ , a₁b₂-a₂b₁)

内積は求めるとスカラーになりますが、外積はベクトルになるので注意です。
また　a×b=-b×a　であり可換ではありません。また、aとka(平行なベクトル)の外積は０になることも確認してください。そして、

a・(a×b)
=a₁a₂b₃-a₁a₃b₂+a₂a₃b₁-a₂a₁b₃+a₃a₁b₂-a₃a₂b₁
=0
b・(a×b)
=b₁a₂b₃-b₁a₃b₂+b₂a₃b₁-b₂a₁b₃+b₃a₁b₂-b₃a₂b₁
=0

となるので、aとbの外積はもとのaにもbにも直交していることが分かります。

つまりaとbの外積とは
aにもbにも直交し、大きさがaとbが張る平行四辺形の面積になっているベクトル
ということです。

a・b=|a||b|cosθ
|a×b|=|a||b|sinθ
内積=0は垂直　外積=0は平行

基本的な学習はこれで終わりです。
あとは問題を解く際に、ベクトルの考え方を使えるように演習をしていきましょう。