ベクトルと中学数学①

ようこそ、クリハロ教室へ
僕はDiscordというSNS上でクリハロ教室の講師をしています。今回は高校受験問題を楽して解くべく、Discordの方ではあまり触れない予定のベクトルを全２回に渡って、学んでいこうと思います。
(僕のTwitterまでDMを頂けると、クリハロ教室に参加できます。興味の湧いた方は是非！)

ベクトルは高校２年生の範囲ですが、簡単な部分だけでも利用できれば、中学生がミスしがちな空間図形などの範囲の問題もスパッと解決することができます。どんな難しい問題も閃き無しの計算問題に早変わり！この裏技を身につけて図形問題を克服または得意にしていきましょう。

＊ ベクトルとその意味

今回は高校範囲の有向線分としての幾何ベクトルを扱いますが、もう少し厳密には大学数学でベクトル空間というものが定義され、それは８つの公理から成り立ちます。

(この公理は今回は読み飛ばして構いません)
集合Vの任意のベクトル　u,v,w
係数体に属する任意のスカラー　a,b として
次の条件が成り立っているとき、Vをベクトル空間と呼ぶ。

　　１、(u+v)+w=u+(v+w) 結合律
　　２、u+v=v+u 可換律
　　３、u+0=u 加法単位元
　　４、u+(-u)=0 加法逆元
　　５、a(u+v)=au+av
　　６、(a+b)u=au+bu 分配律
　　７、a(bu)=(ab)u 乗法の両立条件
　　８、1u=u 乗法単位元

まぁこんな、難しい話は良いとして、図形問題で使える幾何ベクトル(空間ベクトル)を見ていきましょう。
(幾何ベクトルの全体も、ベクトル空間なので、もちろん上の公理を満たします。そのためこの記事でも上記の計算は断りなく使用します。)

注意
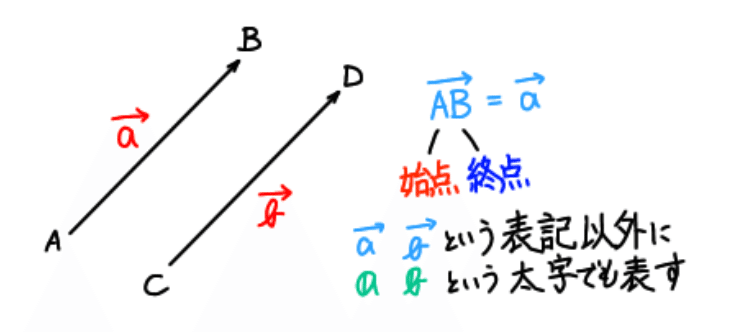
上付きの矢印はnoteでは表せないので、この記事では太字を用いて、ベクトルABやベクトルaを(AB),aという風に表します。

大きさと向きを持った量をベクトル量といい、点Aから点BまでのベクトルはベクトルAB(AB)といいます。
上の図で、点Cと点DはそれぞれA≠C,B≠Dですが(AB)と(CD)が向きが同じで大きさも同じ場合、(AB)=(CD) となります。

つまり、向きと大きささえ同じならどこにあっても同じベクトルです！
(AB)=a , (CD)=b とすると　a=b がいえます。

【スカラー倍(実数倍)】

スカラー(実数)をベクトルに掛けると向きを変えずに大きさを変えることができます。

kを任意の実数として
kaの大きさは単純に、aのkの絶対値倍です。
正の場合は同じ方向、負の場合は反対の方向になります。
よって線分ABとCDが平行であるとき
(AB)=k(CD)と表すことができます。

また、特にk=-1の場合
大きさは同じで向きが反対のベクトルなので終点と始点を入れ替えて　-(AB)=(BA)　といえます。

k=0の場合は大きさが0なので向きを持たず
零ベクトル(ゼロベクトル)となります。
0a a-a (AA) などは 0 となります。

【成分表示】

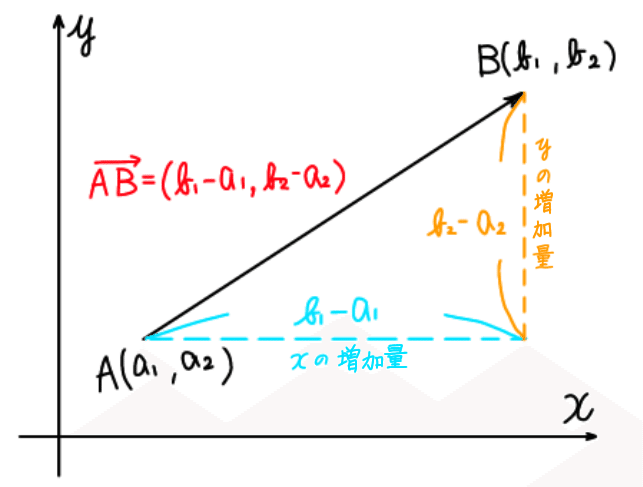
xy平面上の点の座標は(x,y)と書きました。
ベクトルでは始点から終点に向かって、
x座標がu₁増加し、y座標がu₂増加するとき
(u₁,u₂)と書き、これをベクトルの成分表示と言います。成分表示されたベクトルの実数倍は次のようになります。

k(u₁,u₂)=(ku₁,ku₂)

点A,Bの座標を(a₁,a₂),(b₁,b₂)とすると
(AB)=(b₁-a₁,b₂-a₂)となります。

(終点－始点)という形になっていますね。
すなわち、始点が原点Oである(OP)の成分表示は点Pの座標と等しく、これを位置ベクトルと言います。

【ベクトルの大きさ(ノルム)】

a=(a₁,a₂)とすると
xの増加量a₁とyの増加量a₂の大きさを隣辺,対辺とする直角三角形の斜辺にあたる部分がaなので、三平方の定理から、aの大きさ|a|は

|a|=√(a₁²+a₂²)

a/|a|は大きさが１のベクトルで、方向の成分のみを調べるのに適しています。これを単位ベクトルといい、ベクトルをノルムで割り単位ベクトルにする操作を正規化と言います。

＊ 寄り道して和を示せ

u=(u₁,u₂),v=(v₁,v₂)とすると
u+v=(u₁+v₁,u₂+v₂) と定義されます。
図形的に見るとこのようになります。

(AB)+(BC)=(AC)
というように、AからCへ進むのにBに寄り道したような形になっています。例えば
(AB)+(BC)+(CD)+(DE)=(AE)
のように終点に始点を合わせて和を取ると、寄り道をするように、最初の始点と最後の終点を始点と終点とするベクトルになります。

【練習】
正六角形ABCDEFでCDの中点をMとする。
そして　(AB)=a,(AF)=b　とするとき、
(AO),(DF)(AM)をa,bを用いて表そう。

(1)
まず、aやbと平行な線分を辿ってOに行くための道を考えてみよう。例えば、A→B→Oと進めばAからOに辿り着きます。つまり
(AO)=(AB)+(BO)=(AB)+(AF)=a+b

(2)
D→E→O→Fと辿ると
(DF)=(DE)+(EO)+(OF)=-(ED)-(OE)-(FO)
=-a+(-b)+(-a)=-2a-b
反対向きのベクトルもマイナスにして解決

(3)
A→B→O→C→Mと辿ると
(AM)=(AB)+(BO)+(OC)+(CM)
=a+b+a+(1/2)b=2a+(3/2)b
中点ということは、ベクトルの大きさは(1/2)倍になる。

この寄り道の感覚はとても大事です。いくら寄り道しても最後に辿り着けば良いのです！

余力のある人はOを(0,0)、Eを(2,0)などと定義して、各点の座標を求めてから(終点－始点)でベクトルを計算し、確かにaやbの式で表されているか、確認してみましょう。

平面上において
平行でなく零でないベクトルa,bが存在すれば
任意のベクトルpは、実数s,tを用いて

　　　p=sa+tb に一意に示される

このとき、a,bは一次独立であるといいます。

＊ 平行条件と垂直条件

【平行条件】

a=(a₁,a₂) , b=(b₁,b₂) として
aとbが平行ならば　a=kb と表せるので
(a₁,a₂)=(kb₁,kb₂) がいえる

すなわち、　a₁=kb₁ , a₂=kb₂
kについて解いて　k=(a₁/b₁) , k=(a₂/b₂)
つまり、　(a₁/b₁)=(a₂/b₂)

平行条件　
a₁b₂ - a₂b₁ = 0

【垂直条件】

まず、直線の方程式の垂直条件を考えます。

このように証明され、二直線が直交(垂直に交わる)ための条件は、傾き(y=ax+bのaの部分)の積が-1であることと分かりました。

a,bを位置ベクトルになるように平行移動させて、このベクトルを含む直線の方程式を考えると図のようになる。

よって、この傾きの積が-1になるとき、元のベクトルa,bも垂直であるといえる。

すなわち、　(a₂/a₁)(b₂/b₁)= -1
両辺にa₁b₁を掛けて　a₂b₂=-a₁b₁

垂直条件
a₁b₁ + a₂b₂ = 0

特にこの a₁b₁+a₂b₂ のような各成分の積の総和の値を内積といい、a・b と表します。
つまり、内積が０であれば垂直と言えます。

次回はこの内積についてのお話と空間ベクトルを紹介しますので、実際に中学数学の問題で使ってみましょう。

最後まで読んでくださって、ありがとうございました。これが2020年最後の記事となります。2021年もよろしくお願い致します。