
さるぶつ道場 光7解答
2つの凸レンズによる組み合わせレンズ
問題はこちらです.
安易に結像公式(写像公式,レンズの公式)を用いるのではなく,三角形の相似を考えて解き進める.(1)近似式を上手に用いる.(2)Aの実像をBで変換(結像)することに注意する.ただし(4)は,Aがつくる実像を,Bで変換すると考えると解きやすい.
(1)
図3のように,点Aにおける入射角を $${i}$$ ,屈折角を $${r}$$ とする.$${h}$$ に比べて曲率半径 $${R}$$ は十分に大きく,屈折率 $${n}$$ が1よりわずかに大きいので,$${i}$$ も $${r}$$ も極めて小さい角である.したがって,
$$
\begin{array}{}
i & \approx &\sin i=\frac{h}{R}\\
r&\approx &\sin r=n\sin i =n\frac{h}{R}
\end{array}
$$

図3より,
$$
\begin{array}{}
\angle {\rm CAB}+\angle {\rm DAC}+\alpha &=& \frac{\pi}{2}\\
\angle {\rm DAC}+r &=&\frac{\pi}{2}
\end{array}
$$
$${\angle {\rm CAB}=i}$$ なので,上の2式より,
$$
\begin{array}{}
i+\alpha-r&=&0\\
\alpha &=&r-i\\
&=&n\frac{h}{R}-\frac{h}{R}\\
&=&(n-1)\frac{h}{R}
\end{array}
$$
焦点距離は,近似的に $${f=\frac{h}{\alpha}}$$ と近似されるので,
$$
\begin{array}{}
f&=&\frac{h}{\alpha}\\
&=&\frac{h}{(n-1)\frac{h}{R}}\\
&=&\frac{h}{n-1}
\end{array}
$$
(2)
スクリーンに実像が映るとき,図4のように作図されるので正立である.
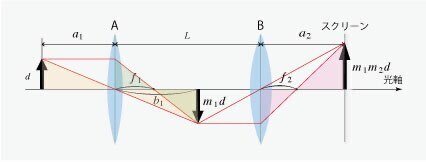
(3)
Aによって作られる実像の長さを $${m_1d}$$ ,Bによって作られる実像の長さを $${m_1m_2d}$$ とする.三角形の相似に注目すると,図3より $${m_1}$$ は,
$$
\begin{array}{}
\frac{b_1}{a_1}&=&\frac{m_1d}{d} \cdots ①\\
\frac{b_1-f_1}{f_1}&=&\frac{m_1d}{d} \cdots ②
\end{array}
$$
①式から,$${b_1=m_1a_1}$$ .②式に代入して,
$$
\begin{array}{}
\frac{m_1a_1-f_1}{f_1}&=&\frac{m_1d}{d}\\
m_1a_1-f_1&=&m_1f_1\\
m_1&=&\frac{f_1}{a_1-f_1}
\end{array}
$$
$${m_2}$$ は,
$$
\begin{array}{}
\frac{a_2-f_2}{f_2}&=&\frac{m_1m_2d}{m_1d}\\
m_2&=&\frac{a_2-f_2}{f_2}
\end{array}
$$
したがって,スクリーンに映る像の長さは,
$$
\begin{array}{}
m_1m_2d&=&\frac{f_1}{a_1-f_1}\cdot \frac{a_2-f_2}{f_2}d\\
&=&\frac{(a_2-f_2)f_1}{(a_1-f_1)f_2}d
\end{array}
$$
(4)

図5よりAがつくる像の位置 $${b_1}$$ は, 結像公式を用いて,
$$
\begin{array}{}
\frac{1}{a_1}+\frac{1}{b_1}&=&\frac{1}{f_1}\ \cdots ③\\
-\frac{1}{b_1}+\frac{1}{a_3}&=&\frac{1}{f_2}\ \cdots ④ \\
\end{array}
$$
③,④式より,
$$
\begin{array}{}
\frac{1}{a_1}+\frac{1}{a_3}&=&\frac{1}{f_1}+\frac{1}{f_2} \\
\frac{1}{a_1}+ \frac{1}{a_3}&=&\frac{f_1+f_2}{f_1f_2}\\
\end{array}
$$
⑤式の右辺が,A,Bを1つのレンズと見なしたときの焦点距離の逆数なので,
$${f_3=\frac{f_1f_2}{f_1+f_2}}$$
(5)
⑤式より,
$$
\begin{array}{}
\frac{1}{a_1}+ \frac{1}{a_3}&=&\frac{f_1+f_2}{f_1f_2}\\
\frac{1}{a_3}&=&\frac{f_1+f_2}{f_1f_2}-\frac{1}{a_1}\\
&=&\frac{a_1(f_1+f_2)-f_1f_2}{a_1f_1f_2}\\
a_3&=&\frac{a_1f_1f_2}{a_1(f_1+f_2)-f_1f_2}
\end{array}
$$
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
