さるぶつ道場 電場と電位1解答

2つの電荷がつくる電場中での粒子の運動

　問題はこちらです．

 (1)，(2)電場はベクトル，電位はスカラーである点に注意しましょう．(3) $${\Delta W=q\Delta V}$$ を用います．電位の定義を思い出しましょう．(4)静電気力は保存力なので，力学的エネルギー保存則が成り立ちます．(5)では無限遠点での電場の位置エネルギーは0である点に注目しましょう．また(4)の結果を上手に使って，解答を表しましょう．

(1)

図2

　O，Cにおける，A，Bの電荷がつくる電場は図2のようになる．

　Oでの電場 $${E_O}$$ は，

$${E_O=\frac{kQ}{(4a)^2}-\frac{kQ}{(4a)^2}=0}$$

　Cでの電場 $${E_C}$$ は，三角形の相似を考えると，図3より $${\cos\theta =\frac{3}{5}}$$ ，$${\overline{\rm AC}=5a}$$ なので，

$$
\begin{array}{}
E_C&=&2\cdot \frac{kQ}{(5a)^2}\cos\theta\\
&=&2\cdot \frac{kQ}{(5a)^2}\cdot\frac{3}{5}\\
&=&\frac{6kQ}{125a^2}
\end{array}
$$

　向きは $${x}$$ 軸負の向きである．

(2)

　Oの電位を $${V_O}$$ ，Cにおける電位を $${V_C}$$ とすると，

$$
\begin{array}{}
V_O&=&2\cdot \frac{kQ}{4a}\\
&=&\frac{kQ}{2a}\\
V_C&=&2\cdot \frac{kQ}{5a}\\
&=&\frac{2kQ}{5a}
\end{array}
$$

(3)

図3

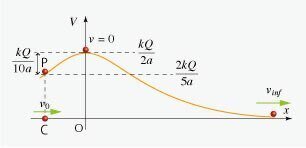
　CO間の電位差 $${\Delta V_{CO}}$$ は，図3より，

$$
\begin{array}{}
\Delta V_{CO}&=&V_O-V_C\\
&=&\frac{kQ}{2a}-\frac{2kQ}{5a}\\
&=&\frac{kQ}{10a}
\end{array}
$$

　したがって，正電荷PをCからOまで移動させるのに必要な仕事 $${W_{CO}$$ は，

$$
\begin{array}{}
\Delta W_{CO}&=&q\Delta V_{CO}\\
&=&\frac{kqQ}{10a}
\end{array}
$$

(4)

　PのCでの電場による位置エネルギー $${U_C}$$ ，及びOでの電場による位置エネルギー $${U_O}$$ は，

$$
\begin{array}{}
U_C&=&\frac{2kqQ}{5a}\\
U_O&=&\frac{kqQ}{2a}
\end{array}
$$

　Pを最小の初速度 $${v_0}$$ で発射したとき，OでのPの速さは0なので，力学的エネルギー保存則より，

$$
\begin{array}{}
K_C+U_C&=&U_O\\
\frac{1}{2}mv_0^2+\frac{2kqQ}{5a}&=&\frac{kqQ}{2a}\\
\frac{1}{2}mv_0^2&=&\frac{kqQ}{10a}\\
v_0^2&=&\frac{kqQ}{5ma}\\
v_0&=&\sqrt{\frac{kqQ}{5ma}}\\
\end{array}
$$

(5)

　Pの無限遠方での運動エネルギーを $${K_{inf}$$ ，電場による位置エネルギーを $${U_inf}$$ とする．力学的エネルギー保存則より，

$$
\begin{array}{}
K_C+U_C&=&K_{inf}+U_{inf}\\
\frac{1}{2}mv_0^2+\frac{2kqQ}{5a}&=&\frac{1}{2}mv_{inf}^2+0\\
v_{inf}^2&=&v_0^2+\frac{4kqQ}{5ma}\\
&=&v_0^2+4v_0^2\\
v_{inf}&=&\sqrt 5v_0
\end{array}
$$