
さるぶつ道場 力のつりあい1解答
滑車を利用して台ごと引き上げる人
問題はこちらです.
まず力を図示することが大切です.このとき作用反作用の法則を考えるようにしましょう.この問題では,人が台を押す力 " $${ -N }$$ "(その反作用が人が台から受ける垂直抗力 " $${N}$$ ")を忘れてしまう人が多いので注意しましょう.
台が床から離れるときは,台が床から受ける垂直抗力が0になることや,人がロープを引き続けるためには,人が台から離れないこと(人が台から受ける垂直抗力が正)というような条件を,文章から読み取りましょう.
a 図1のように,ロープの張力を $${T}$$ ,人が台から受ける垂直抗力を $${N}$$ ,台が床から受ける垂直抗力を $${n}$$ とする
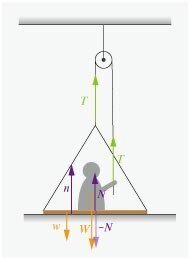
鉛直方向の力のつりあいは,
人:$${T+N-W=0}$$ …①
台:$${T+n-w-N=0}$$ …②
台が床から離れるとき $${n=0}$$ なので,上の2式から,
$${2T-W-w=0}$$
$${T=\frac{W+w}{2}}$$
①式の $${T}$$ に代入すると,
$${\frac{W+w}{2}+N-W=0}$$
$${N=\frac{W-w}{2}}$$
人がロープを引き続けるためには $${N>0}$$ でなければならないので $${W>w}$$ が条件である.
b aと同様に力を図示すると,図2のように表される.
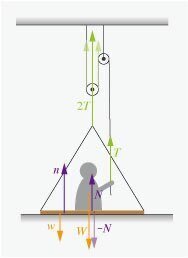
力のつりあいは,
人:$${T+N-W=0}$$ …③
台:$${2T+n-w-N=0}$$ …④
台が床から離れるとき $${n=0}$$ なので,上の2式から,
$${3T-W-w=0}$$
$${T=\frac{W+w}{3}}$$
③式の $${T}$$ に代入して,
$${\frac{W+w}{3}+N-W=0}$$
$${N=\frac{2W-w}{3}}$$
人がロープを引き続けるためには $${N>0}$$ でなければならないので,$${2W>w}$$ が条件である.
詳しい説明はテキストを参考にしてください.
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
