
デジタル一眼カメラにおけるボケの考察~フルサイズとAPS-Cの比較~(最終更新日:2023,Jun.25)
1.はじめに:本記事の目的
CANON EOS R6とR10 (いずれも所有している) を比較していて気になったので、所謂ボケについて調べてみた。
よく知られたようにボケを活かした表現はポートレート撮影やマクロ撮影で撮影テーマ/主要被写体の強調や視線誘導手段として使われる。
より大きなボケを使うことで、強調効果が強くなると考えられる。
そして「大きくボカす」ために使われる手法として、
・撮像素子が大きい方がボケやすい (例:フルサイズ>APS-C)
・明るいレンズの方がボケやすい (例:F1.4>F4.0)
・レンズの焦点距離が長い方がボケやすい (例:70mm>35mm)
・被写体から背景までの距離が長い方がボケやすい (背景ボケの場合)
これら「定性的」な表現としては直感的に理解できる。
ではフルサイズとAPS-Cのカメラで「どの程度、ボケ量が違うのか?」を「定量的に」把握しておくことは、以下の様な状況で有意義と考えられる。
・フルサイズのカメラが使えない時、APS-Cで代用する際にも同じぐらいのボケを使いたいが、どうすれば良いか?
・ボケを重視してカメラを買う際にどの程度の投資が必要か?カメラに投資するか、レンズに投資するか?
これらの疑問に答えを出すことが、この記事の目的である。
2.ボケ量の考察
1) ボケとは何か
ピントが合っていない場所にある被写体 (点の大きさ) が、撮像素子上で1点に結像せず、広い範囲に映像として記録される範囲をカメラ用語で「錯乱円」と言う。 (下図参照)

ではボケとは何か?ボケという言葉は「暈ける」「ぼやける」という言葉から出てきたもののようである。
すなわち、元々は「暈けている状態」を示す言葉であったものが、いつ頃からか名詞のように扱われるようになった。
ボケの量とは、錯乱円の大きさに「近い」と言える。同じでは無いと考える。
なぜなら、錯乱円の大きさはあくまで撮像素子上で測定される。
だが、写真は本来、撮像素子で検知された光学信号を何らかの媒体上に投影して鑑賞するものである。
その「鑑賞可能状態」での「錯乱円の大きさ」がボケの量と言える。(下図参照)
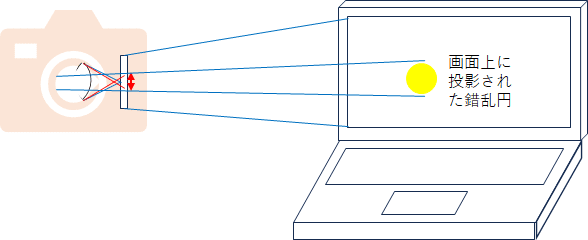
以下では、そのような定義で論を進める。
2) ボケ量の計算
ボケ量の算出については、すでにいろいろなページで紹介されている。
https://analogstd.com/photography/relationship-between-bokeh-and-focal-aperture
それでも敢えてこの記事を書いているのは、R6 (フルサイズ)とR10 (APS-C)の比較のための理論値を定量的に導出したかったためである。
撮像素子上での錯乱円の直径を計算する式は以下である。
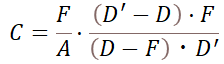
式1で、
Cは、撮像素子(フルサイズ) 上での錯乱円の直径
Fは、フルサイズカメラに付けたレンズの焦点距離
Aは、フルサイズカメラに付けたレンズの絞り値
Dは、フルサイズカメラから被写体までの距離
D’は、フルサイズカメラから背景(暈かしたいもの) までの距離
である。
次に、同じ式をAPS-Cカメラについて書いた式2を挙げておく
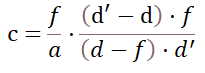
式2で、
cは、撮像素子 (APS-C) 上での錯乱円の直径
fは、APS-Cカメラに付けたレンズの焦点距離
aは、APS-Cカメラに付けたレンズの絞り値
dは、APS-Cカメラから被写体までの距離
d’は、APS-Cカメラから背景(暈かしたいもの) までの距離
である。
式1と式2は、数式としては同じものである。
3) フルサイズとAPS-Cのボケを同じにする
本節冒頭に書いたように、論じたいのは「鑑賞可能状態」での「錯乱円の大きさ」である。
鑑賞方法は鑑賞者それぞれで異なる。だが、鑑賞可能状態にした時の錯乱円の大きさをフルサイズのカメラで撮った画像と、APS-Cのカメラで撮った画像の間で、同じ尺度で測る方法として、撮像素子の寸法に対する錯乱円の大きさの比率を考えることが出来る。
例えば、フルサイズの撮像素子の大きさは、一般的に24mm x 36mmである。
よって、フルサイズの撮像素子の短辺に対する錯乱円の大きさの比率は、式1から、C÷24で表現できる。
同じくAPS-Cの撮像素子の大きさは、キヤノン製カメラの場合、14.9mm x 22.3mmである。これを近似的に15mm x 22.4mmと考える。
そうすると、APS-Cの撮像素子の短辺に対する錯乱円の大きさの比率は、式2から、c÷15で表現できる。
さて、フルサイズのカメラとAPS-Cのカメラで、同じ被写体を同じ撮影距離から「同じ画角で」撮影する場合を考える。
この「同じ撮影距離」という仮定を置いたのは、撮影距離を自由に変えられない場合が存在するからである。
また「同じ画角」という仮定をおいたのは「被写体をどの程度の大きさで撮像素子上に結像させるか?」は「表現意図」から決定されるからである。
これらはポートレート撮影においては、「同じ撮影距離」で「同じ画角」が求められることが多いという現実からも適切な仮定と考えている。
例えば、しばしば「標準レンズ」と呼ばれる焦点距離50mmのレンズをフルサイズカメラに取り付けて撮影した画像と、同じ撮影距離で同じ画角の画像をAPS-Cカメラで撮影するためには、焦点距離31.25mmのレンズを使う必要がある。
この関係を数式で表すと、式3の様になる。Fとfの意味は、式1/2と同じである。
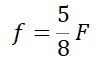
フルサイズのカメラとAPS-Cのカメラで撮影した「同じ画角」の写真の「鑑賞可能状態」での「錯乱円の大きさ」が同じ (つまりボケ量が同じ) である場合を数式として表現すると、以下の様になる。
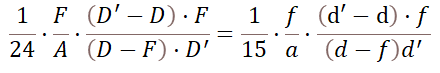
式4で、F/A/D/D'/f/a/d/d'の意味については、式1および式2と同じである。但し「同じ撮影距離」という仮定をおいたので、D=d、D'=d'である。
更に、Fとfの関係については式3で定義されるので、これらD/d/D'/d'/F/fの関係を式4に代入して整理すると以下の様になる。
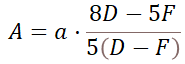
この式の分子 (8D-5F) は、「撮影距離の8倍から焦点距離の5倍を減算する」であるが、ポートレート撮影では撮影距離は数m、焦点距離は数十mmであり、8D-5Fはほぼ8Dと同じである。
同じ理由から、分母もほぼ5Dと同じである。
よって、次の式が出来る。

フルサイズカメラとAPS-Cカメラで「同じ撮影距離」で「同じ画角」で撮影する場合、フルサイズカメラの絞り値の1.6倍(つまり撮像素子の大きさの比率)と同程度のボケになるということだ。
3. 結論:ボケを活かすならやっぱりフルサイズ
つまり例えば、フルサイズでレンズ絞り値2.0で撮影したのと同じ条件(撮影距離、画角)で、同じボケ量の写真をAPS-Cで撮影するためには、APS-Cのレンズの絞り値は、1.25となる。
ただし、気をつけないと行けないのは、フルサイズの焦点距離50mmの画角は、APS-Cでは焦点距離30mmぐらいになるので、
焦点距離30mmで開放F値1.25なんていうレンズは存在しない
ってことだ
「お金がないからAPS-Cカメラを買う」はもちろん否定しないが「ボケを活かした写真を撮りたい」なら、寧ろ安価なフルサイズカメラを買う方が現実的である場合もある
更新履歴
2023/06/25 誤記訂正
2023/06/20 新規公開
