
徒歩で『メネラウスの定理』を証明してみた
※この記事は
鉄道を使って『メネラウスの定理』を証明してみた
の続編です
■前回のあらすじ
容赦なく浴びせられる銃弾と爆風の嵐──
街のあちこちで巻き上がる炎は、敵陣営の勝利を祝う舞を踊っていた。
辛うじて逃げ延びているデイブレイク軍の残滓。次に背中にタマが撃ち込まれるのは誰か……。その緊迫感の中、俄に立ち止まり後ろを振り返った男がいた──いや、彼にとっては“前を向き直した”だけだ──……シノ=ノーメスだ。
「どうしたシノ! 休んでるヒマは……ま、まさか……!!」
『……私は子供の頃、“コンピュータ人間”なんて渾名を付けられましてね……』
「無茶な真似はよせ!! お前、……天才数学者なんだろ……? こんな状況じゃ俺らにはどうすることもできねえって、証明されてるようなモンじゃねえか!! お前ほどの頭脳なら……そんなこと……」
『ええ、勿論わかっています…………だが“コイツ”がわからないそうですよッ!!』
彼は太腿をパンと叩いて駆け出し、豪煙の中へ消えていった。
「シノ!!!!!」
「待て! ……見たか? “コンピュータ人間”のアツいハート、いや、ハムストリングスをよ……」
「……ああ……」
「……俺らはどうだ?」
「…………そうだな……俺も同じだよ…………奴等の今日のディナーは、大盛りのローストハムかもしれねえなァ!!」
彼らもまた“前”を向いて走り出し、豪炎の中へ飛び込んだ──
■証明手法を確認
シノとその同僚たちの両脚はバカでしたが、東雲の両脚はかしこいのでメネラウスの定理を証明します。
まずは、徒歩でメネラウスの定理を証明するその手法を確認しよう。


基本的には前回と同じで、各区間の徒歩時間を計測し、メネラウスの定理に当てはめ、成立することを確認するだけである。
また、例によって東急大井町線区間と東急目黒線区間はどちらか一方のみ計測すればいいが、念のたゴホンゴホンどちらを採用する場合でも成り立つことを示し東雲の徒歩の圧倒的精確性を知らしめるために、計測しておく。
徒歩時間の計測においても、以下のようにルールを設けた。
アップダウンの平面変換? 踏切・信号待ち? うるせえ! 俺の脚はかしこいんだからそんなのも計算ずくだ! ストップウォッチは止めねえ!
徒歩はタダ? 5往復できる? うるせえ! 俺の脚はかしこいんだから一発で充分だ! 1回しかやらねえ!
朝ご飯? 鮭の塩焼き定食だ! 美味しいよねえ!

■俺の一歩一歩が震源地だぜ
ということで、早速計測しにいこう。
しかし、徒歩でメネラウスの定理を証明、か……。前代未聞、前人未到、唯一無二、混浴風呂……そんな言葉が似合う。東雲が繰り出すマグニチュード5兆の徒歩力が、数学界に激震を与えるぜ……。これから数時間、途切れることなく数万回の激震が発生し、気象庁は震源地の分布を見て驚愕する──それはまさしく、メネラウスの定理を想起させるキツネ顔が浮かび上がるからだ。これが俺の論文代わりさ──
ちょっとその前に
行かなければならない場所がある。それは……

千代田区にある、日枝神社である。
東京から日光まで歩きにいく前、今までにない厳しい闘いになると予想されたので、自分の中で交通安全のイメージがあった日枝神社にお参りして、無事達成して帰れるようにお願いしたのだった。そして結果は皆さんご存知の通り、VICTORYである。
日光の最終盤で、降ってきた雨に対して「神様が感動して泣いておられるのかもしれない」というトークをしたが、あれは日枝神社の神様を意識したもので、どこかで事前参拝エピソードを話すための伏線にしておこうと、ノープランで種を蒔いていたのである。
今回歩く総距離ははっきり言って鼻クソだが、かなりブランクがあるし、色々あって体型も随分変わってしまった。何が起こるかわからない。
財布からなけなしの御縁玉を取り出す。すみません、今の俺にはこれしか……
パンパン
「日光の時はありがとうございました。今回も無事達成できますように!!」

■さあ、証明しよう──メネラウスの定理と、徒歩の復活を
前回同様、自由が丘出発で、大岡山→大井町→目黒→渋谷→自由が丘→田園調布→大岡山→目黒の順に歩いていく。
※各区間の所要時間は後でまとめて発表します
【自由が丘→大岡山】

写真の空気感からわかるように、夕方スタートである。朝食の鮭は最早関係なくなっているだろう。
私は、何年か振り(ちゃんと調べろ)の一歩を、この自由が丘駅正面口から踏み出した。
アタック!東雲は「鉄道×徒歩」ジャンルの元祖にしてレジェンドであると評価する人もいる。もちろん嬉しいし、誇りたいことであるが、驕ってはいけない。今の私は別人と思おう。再びここから鍛錬を積んで、鉄道系歩行者界の最前線に復帰するのだ。長い距離にこだわらなくていい。不眠にこだわらなくていい。歩みを止めないことだ。少しずつでも、続けられるかたちで続けること……とにかく“立ち止まらない”ことが何よりじゅ

オイイイイイイイイイイ!!!!!!!
俺が一歩一歩を踏みしめながら心の中で決意を新たにしている時に!! ボケ洪水の中に気休め程度の感動シーンをつくろうとしている時に!! 始まって何分、いや何秒だよ!?

フ、フン、まあいいさ……なんせ俺の脚はかしこいからな……発揮し甲斐があるってもん

テメエエエエエエエエエ!!!!!!
二度しかない踏切で二度止めやがって……!!
いやまあわかりますよ、東雲の徒歩と言えば鉄道と最も競合する移動手段スもんね? そりゃあ東急さんも全力で邪魔しますよね〜〜〜だってレジェンドっスから〜〜〜(早速驕っていく)


短いくせに無駄に時間喰った気がするけど、とりあえず到着。
【大岡山→大井町】
この辺は住宅街だし、道に気を付けながら行きましょ。

東京あるある:住宅街にV字谷ありがち

中原街道と交差。太い道を渡る時の赤信号は出来れば引きたくないところ。

東雲あるある:細い裏路地撮りがち


荏原中延駅至近のこの公園は、すぐ下に東急池上線が通っている。本当にすぐ下で地面は皮膚程度の厚さしかないので、鉄道に注射したい時はこの公園を利用するといい。

国土交通省は感謝しなければならない。もし私が究極の精確性を見せるために男塾名物・直進行軍をしていたら、あの中央分離帯は木っ端微塵になっていた。本来起こる予定だった損失を回避してやったのだから、浮いた修繕費用を私の口座に振り込むべきである。



もうええわ!!!!!!!!

……と見せかけて、この踏切は渡る必要がない。私が踏切渡りフェイントをした瞬間、慌てて遮断棹を下ろしてきたのだ。東急もケッコーかわいいとこあんじゃねえか(cv:諏訪部順一)

みんな大好き下神明トライクロス。今名付けた。
今回は駄目だったが、この前フラッと来た時は何も狙ってないのに東海道新幹線・品鶴線・大井町線が同時に全部来た。なんて俺は幸運に恵まれた男なんだと感慨した。
ちなみにその日、家を出て5秒で車に水をかけられ、チャーシュー麺のチャーシューを忘れられている。

帰路につく人々で賑わう大井町に到着。
【大井町→目黒】
休憩は一切しない。道中はもちろん、ペースが乱れるため区間の境でもしないので、意外とハードな旅である。

夕暮れの都会を、JR東京総合車両センター越しに望む。


ついさっきまで住宅街だったのに、少し歩いただけで高層ビルがバンバン建つ。街は紙一重に形成されていくのだな……
てか全部の信号引っかかってないか???

五反田駅手前の山手線高架下の壁画。未来行きとのことで、超長時間運転のようだが、果たして使用車両は103系でよかったのだろうか……?
いや、国鉄・JRを長年支えた代表的な車両として「未来まで語り継がれる」だろう、ということを表現しているのかもしれない。




ちなみに目黒駅は目黒区ではない(品川区)。こういうのは東京ではよくある。
更にちなむと、その品川区に品川駅はない(港区)。
【目黒→渋谷】

なんか見所なくてもう着いちゃいました。
じゃあ、尺稼ぎになぞかけでもしますか……
え〜では
徒歩に命をかけまして〜
2本の宝刀の封印をときます
その心は!?
ウォーク(多く)のファンが待ってるから……///


【渋谷→自由が丘】
最長区間である。ここを乗り切ればだいぶ楽になる。

渋谷駅周辺は魔境みがあったが、それでもまた少し歩けば閑静な住宅街である。東京は狭いねえ……

祐天寺と池尻大橋の真ん中ぐらいに蛇崩(じゃくずれ)交差点がある。目黒区が生活圏と思われるさまぁ〜ず三村が、「どこ住んでんの?」と聞かれると「蛇崩の近く」と答える人が多いと内村さまぁ〜ずで言っていた。重要な通りが交わるポイントなのでこの辺りの人は皆知っているだろうし、説明に使うのにちょうどいいのだろう。
ちなみに地名としての蛇崩は今や存在せず、上目黒にあたる。


極太道路が建設中なのを発見した。


ここをブチ抜く予定らしい。何とも大掛かりだ。
途中の校庭みたいな所は、台形の面積を求める練習以外の用途が無くなっていそうだがいいのだろうか?


フッフッフッ、私がもし男塾めいぶ

前回、学芸大学に学芸大学はないという件があったが、首都大学東京が東京都立大学となり再び現実が駅名と合致したにもかかわらず、やはり都立大学に都立大学はない。


一周してきました。
【自由が丘→田園調布→大岡山】
短い区間が連続するので、大岡山まで一気に行っちゃいましょう。

もういいスて。。。。。。
しかもまた両側から来ますやん。。。これもう好きじゃんね? 好きな人にいじわるしたいっていうヤツでしょ? 東急と255系のラブコメ漫画描くか????






正直、自由が丘・田園調布・大岡山のトライアングルが小さすぎるんですよ。だから一歩が担う重みが全然違う。これが昨今世間を騒がせている「一歩ょうの格差問題」である。


大岡山は大岡山にない(大田区北千束)。と言っても駅前の道路を渡ったら目黒区大岡山だけどね。
【大岡山→目黒】
いよいよラストである。ちょっと長いけどガンバルゾー!

荏原中延の時と同じように、この公園のすぐ下を東急目黒線が通っている。すぐ下がトンネルの時、地上は公園か駐車場になりがちである。街中に急に細長い公園や駐車場が現れたら、真下に線路や地下道がないか探ってみよう。


大岡山の1つ目黒寄りは「洗足」である。一方、大井町線で大岡山の1つ大井町寄りは「北千束」である。「せんぞく」に2種類の表記があることを不思議に思った人も多いだろう。中世、この辺りは「荏原郡千束郷」という地名であったが、この地にあった大池で日蓮が足を洗ったという伝説から、この大池は「洗足池」と呼ばれるようになり、千束の一部地域は「洗足」と書き換えられるようになったという。
(2022年9月9日参照)
ちなみに洗足池は大田区南千束にあり、洗足・北千束・南千束の中では洗足が洗足池から最も遠い。謎である。

過去の実績で驕ってはいけない、またイチからのスタートだ! みたいな感じで始めていたが、実はナメ腐っていて、ケツに摩擦軽減クリームを塗ってこなかった。その結果、もうケツが擦れて痛い。多分今種田ぐらい股開いて歩いてる。皆さんは5〜6時間ぐらいの徒歩でも油断せずにクリーム塗ってくださいね。

住宅街を歩く時あるあるとして、お風呂の音だけ丸聞こえがちというのがある。換気のために窓を開けている人が多いからなのか、シンプルにシャワーがうるさいからなのか、真相は湯けむりの中だが、お風呂で歌うのはやめとこう……と思った。
あと、お風呂のいい匂いも漂いがち。

正直ちょっと疲れてきた。ケツも痛いしペースが乱れてる気がする。俺の力はここまで落ちたのか……
歌を歌ってテンポを揃えよう。今日のテンポに合った歌は……
♪なんのためーにーうーまれてー♪
♪なーにをしーてーよーろこぶー♪
……
わからねえ……
やめよう……

山手通りだ! これを越えればもう少しで到着するぞ!

ラストぉーーーーー!

おい誰だ最後坂来るようにしたの!!!(お前や)



終了〜〜〜!!
ふぃ〜〜疲れた〜! さっ、か〜えろ!(駅の写真1枚撮って即帰宅)
■ま、余裕でしたね
数時間程度なのに達成を願って神社に行ったり、実力低下実感謙虚発言をしたり、人間アピールをするのも一苦労だぜ……。今回の計測はTAS(Toho Assisted Shinonome)が行ったのだ。しんどいとか大変だとかいうことは実際有り得ない。読者サービスの一環でそういう演出をしていただけである。まったく俺は罪なヤツだぜ(ケツにオロナインを塗りながら)
それでは、TASによる各区間の徒歩時間を確認してみよう。

ということで、前回同様まずは東急大井町線を採用して計算……していきたいところだが、日枝神社の神様から「東急目黒線から先にやったほうがいいよ」とお告げがあったので、仰せの通りにします。
東急目黒線を用いる場合
東急目黒線を使うかたちでメネラウスの定理に各区間を当てはめると、このようになる。

ここに各区間の徒歩時間を当てはめると、

さあ東雲フリークの諸君、フィールズ賞受賞が決定する瞬間に刮目しなさい!!
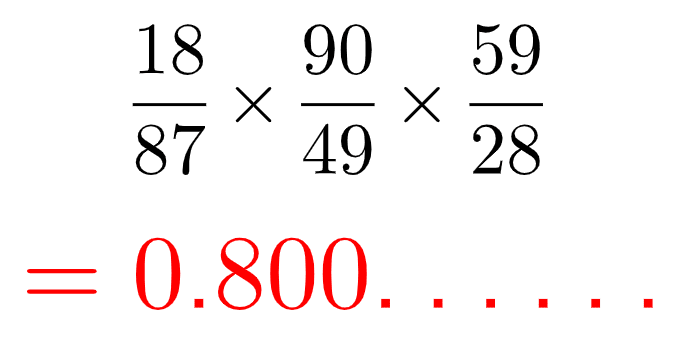
この計算結果をpと置く。
メネラウスの定理が主に登場するのは受験の場面であり、受験と言えば「8割で充分」というスローガンが定番である。天下の理三でも、総合で8割取れれば"余裕で"合格できる。つまり、8割取ろうが満点を取ろうが同じである。従って、
8割 = 10割
割 ≠ 0であるため、
8 = 10
⇔ 0.8 = 1 ・・・①
また、pは0.8に等しいと言っても過言ではない。・・・②
①、②より、p = 1であり、メネラウスの定理が証明された。(Q.E.D.)

証明としては既に充分なのだが、東雲の徒歩の圧倒的精確性を示すため東急目黒線・東急大井町線どちらを通るパターンでも行うと余計なことを言ったので、次は東急大井町線の場合で証明する。
東急大井町線を用いる場合
メネラウスの定理に各区間を当てはめると、

各区間の徒歩時間を代入すると、

計算すると、

ッスゥ~~~………………
(惜しくもないな……どうこじつけるか……?)
…………

先程の計算結果をqと置く。qの値は、三角関数表を見ると、ほぼtan67°である。
ところで、以下の図を見てほしい。
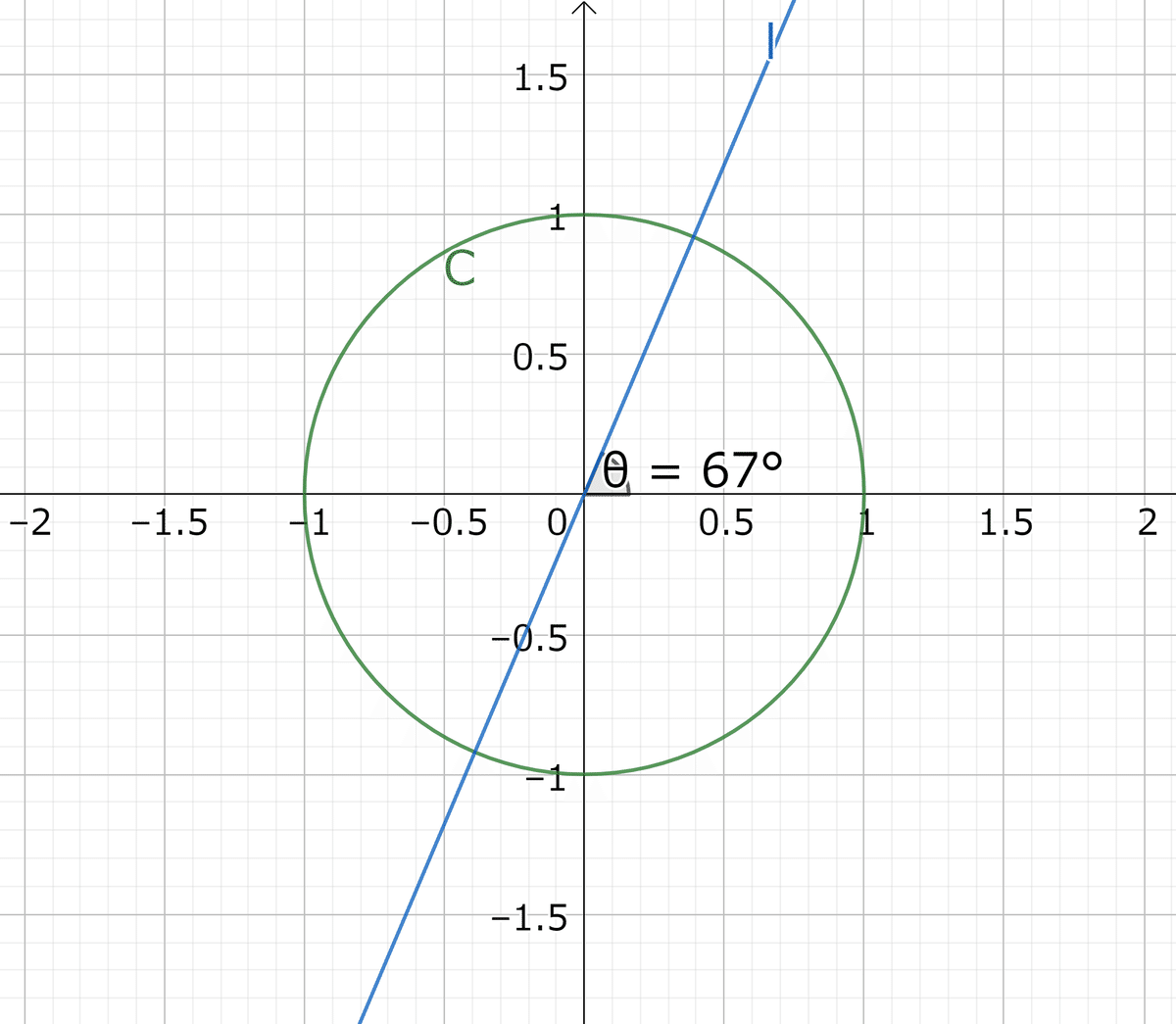
xy座標における円Cと直線lである。
直線lとx軸のなす角が67°であることから、直線lの傾きはtan67°であり、qとも表せる。
この図が何を表しているか、皆さんはもうお解りだろう。
そう、地球である。
地球の自転軸、即ち地軸は、公転面に対して約66.6°、つまり67°傾いており、円Cを地球と見做すと、直線lと完全に一致する。qは、地軸の傾きを表していたのである。
ところが、実はqは他のものも表していた。
さて、メネラウスの定理においては、各分数の分子と分母を逆にしてもよい。従って、

となり、今回の計測結果は0.423であったとも言える。
しかし、これは真実ではない。
この結果は、実際は23.4だったのだが、地球が傾いていることにより数字が全て右に転がってごちゃごちゃに集まった結果順番があべこべになり、更に整数部に数字が無くなったため無を表す0が充填され、0.423になってしまったのである。
そして、今回の徒歩は、とても暑い日本、つまり夏の北半球で行われた。
夏、北半球、23.4……これらが何を表しているかは明白である。
qは、夏至の北回帰線をも表していた。
公転面に対する地軸の傾きを66.6°とした時、北回帰線は北緯23.4°に位置する。夏至の北回帰線における最も特徴的な現象と言えば、太陽の南中高度が90°になることである。
ここで、「太陽の南中高度が90°」を言い換えてみたい。
まず、「90°の空中にある太陽」と言い換える。
太陽はsunであるため、頭文字を取ってsと置くと、「90°の空中にあるs」となる。
そして、語句中の「空」を「何もないこと」の意味で捉えると、ないのと同じなのだから、消去することができる。従って、「90°の中にあるs」と更に言い換えられる。
これを英訳すると、

「sin90°」となる。
当然、sin90° = 1 である。
従って、qはなんやかんやで結局1を表していたのである。
以上より、東急大井町線を用いる場合でもまた、メネラウスの定理が証明された。(Q.E.D.)
前回も述べた通り、古代ギリシャの数学者であったメネラウスは、天文学者でもあった。そんな彼が示したメネラウスの定理の証明に、地球、太陽が用いられる──
果たしてこれは、「偶然」だったのだろうか──?
■またひとつ歴史に名を刻んでしまった
かくして、東雲の徒歩によるメネラウスの定理の証明は、大成功を収めたのであった。
いや、成功とか失敗とかの話ではない。当たり前のことなのだ。私の完璧に論理的な両脚が、普通のことを普通にやっただけなのである。もしかしたら皆さんは、歴史に名を刻んだところで「でしょうね」としか思っていないかもしれない。大変申し訳ない。至極当然の内容がひたすら続く、長いくせに平坦で面白みのない文章をお見せしてしまったことに対し、深くお詫び申し上げます。
それでは皆様、淡々と↓のページの編集準備をお願いいたします。
https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A3%E3%83%BC%E3%83%AB%E3%82%BA%E8%B3%9E
■茶番はここまで
正直これと同レベルのクソガバ論理(笑)を大真面目な顔で展開する人大勢いるやろ。みんなは引っかからないように、そして自らもクソガバ論理を展開しないようになという啓発の記事だったのである(違います)
ということで、前回も合わせて1万字を超える茶番にお付き合いくださりありがとうございました。ここからは真面目タイムです。
■徒歩の振り返り
今回歩いたコースはこのようになっています。

まあ……プールに潜ったキツネの顔見たらこんな感じだと思うんで、綺麗なキツネ顔なんじゃないですかね……?
総距離29.7kmということで、これは東京~大宮とほぼ同じです。東京から大宮まで行くだけで「ふぃ~~疲れた~」とか情けないにも程がありますね。
あと、いつも計測している歩数なんですが、なんか歩数計アプリが調子悪くて途中で止まってしまったので、今回はありません。
ところで、今回の話には東雲の徒歩の精確性が重要なテーマとしてあったわけですが、実際精確だったのでしょうか。各区間の徒歩スピードを確認してみましょう。
【自由が丘→大岡山】
1.9km/22分 5.2km/h
【大岡山→大井町】
4.9km/65分 4.5km/h
【大井町→目黒】
4.1km/49分 5.0km/h
【目黒→渋谷】
3.3km/41分 4.8km/h
【渋谷→自由が丘】
7.1km/87分 4.9km/h
【自由が丘→田園調布】
1.4km/18分 4.7km/h
【田園調布→大岡山】
2.4km/28分 5.1km/h
【大岡山→目黒】
4.6km/59分 4.7km/h
【総合】
29.7km/6時間09分 4.8km/h
まあそりゃ精確じゃないですね()
さすがに信号とか踏切の待ち時間を考慮してペースを調整するなんて技術は持ってません。ストップウォッチをいちいち止めるのをめんどがらなかったら、また違ったかもしれないけど……
あと総合で時速4.8kmとのことですが、これは東京から日光まで歩いた時の冒頭30kmの速度とあんま変わんないですね。つまり、全盛期におけるケツに100km以上控えてる状態で出すスピードが、今のMAXになってしまっていると……
ちなみに2回目の足柄駅乗換(25.3km)の時は、平地パートで時速6.4km、山下りパートで時速6.9km、山上りパートでも時速5.5km出してるので、やはり明らかに実力低下してます。
まあまあ、何年も休んだ後の一発目なんでね……また慣れていけば速くなるでしょ。輝く宝も磨かなければくすむということで、これから毎日キュッキュしようぜ?
ちなみに、地図上でもキツネ顔に見えるかは別として、線路を真っ直ぐにすればキツネ顔になる場所は他にも存在するので、探してみてください。
■一応真面目に証明します
その前に、前回の冒頭で触れた「拡張版」の話をします。
まず、「キツネ顔の図形」を、三角形ABCと直線lによってなされる図形と見做します。直線lと、直線AB、直線BC、直線CAの交点をそれぞれ点P、点R、点Qとします(各交点は全て異なるとする)。

これは、ここまで使ってきた、いわば「通常版」ですが、交点が三角形ABCの各辺上にひとつもなくても構いません。即ち、以下のような場合でも同様に成立します。これが「拡張版」です。

ただ、よく見ると拡張版もキツネ顔になってはいることがわかると思います。つまり、鉄道路線のほうのキツネ顔も拡張版だったと見做すと、また別の計算結果が数パターン得られたかもしれませんが、茶番が複雑になりすぎるのでやめました。
それでは証明してみましょう。なお、通常版・拡張版どちらも同じ方法で証明できます。
※カジュアルな書き方で失礼します
まず、点Cを通り直線lと平行な直線mを引き、直線mと直線ABの交点を点Dとします。


三角形BDCと三角形BPRはいわゆる「ピラミッド型の相似」であるため、

2行目の式を①とします。
また、三角形AQPと三角形ACDも「ピラミッド型の相似」であるため、

2行目の式を②とします。
※「ピラミッド型の相似」では以下が成立します
①、②は下図の3番目を利用して導かれています

①、②より、

となり、メネラウスの定理が証明されました。
noteで数学の証明を見やすく書くの難しいですね……。よくわからないという方はもちろん質問していただいてもいいですし、調べればもっと見やすいサイトがわんさか出てくるので、検索してみてください。
最後に、興味のある方向けの発展問題を用意しました。暇な時に解いてみてください。
解説投稿はいつかやる……かも?
〔発展問題〕
問1
「通常版」におけるメネラウスの定理の逆を証明せよ。
即ち、三角形ABCにおいて、辺AB上に点P、辺AC上に点Qがあり、辺BCの延長線上に点Rがある場合に、以下の式が成り立つ時、点P、点Q、点Rが一直線上にあることを証明せよ。

問2
下図の四角形ABCDにおいて、∠DABの大きさは150°、∠ABCの大きさは60°、∠BCDの大きさは90°である。辺BCの長さが辺ABの長さの5倍である時、辺CDの長さは辺DAの長さの何倍か。(2022 灘中)
※問題文の表現を一部改変しています

この記事が気に入ったらサポートをしてみませんか?
![アタック!東雲 [鉄道系歩行者]](https://assets.st-note.com/production/uploads/images/64809939/profile_22010e87d6e69e22d35c251775ade79e.jpg?width=60)