
物理学概論:量子論
私たちが日常生活で見かけるような物体の運動は,ニュートン力学によってよく記述できることが知られています.運動の三法則をもとに,地上にあるボールやバネといった身近な物体だけでなく,遠く離れた巨大な天体の運動までも記述できるこの理論を用いると,初期条件さえわかれば原理的には宇宙のすべての物質についてその後の状態を予言できるように思われます.
1812年,フランスの科学者ピエール=シモン・ラプラスは,宇宙にあるすべての物質の状態を知っていて,その未来をすべて予言することのできる超越的な存在を考えました.ラプラスの魔物と呼ばれる存在です.あらゆる物質について物理学にもとづいてその時間発展を記述できるなら,宇宙にあるすべての物質に対して,初期条件をもとにその未来すべてを予言できることになります.宇宙が始まったときから,宇宙の未来はすべて決まっているという考え方です.

https://unsplash.com/photos/bnZ8_95Q8NE
しかし,20世紀に入って新たに台頭した理論により,未来を予言することは原理的には不可能であることが示されるようになります.量子論です.量子論は,原子に相当するようなきわめて微小なスケールにおいて,物質を構成する粒子や光などの振る舞いを記述できる理論です.
原子の大きさは10のマイナス10乗メートル程度です.どれくらいのスケールかというと,直径1センチメートルほどのビー玉を地球程度の大きさにまで拡大したとき,ようやく野球のボールと同じくらいのサイズに相当するような,ごくごく小さいスケールです.原子を構成する原子核や電子の大きさはさらに小さいことになります.

量子論では,私たちの日常生活にもとづく常識とは大きく異なる現象が起こることが知られています.たとえば,ミクロな物質や光は波の性質と粒子の性質を併せ持つと考えられています.いわゆる波と粒子の二重性です.また,ミクロな物質や光は,同時に複数の場所に存在することができ,状態の重ね合わせとして表されます.今回はそんな不思議な性質を示すミクロな世界を記述する量子論について紹介していきます.
光の波動性と粒子性
1807年,イギリスの物理学者トーマス・ヤングは,位相のそろった光を二つのスリットに通すと,その先で干渉縞ができることを明らかにしました.ヤングの実験と呼ばれます.光が粒子だとすると,スリットの先に用意されたスクリーン上では光源と二つのスリットの延長線上のあたりだけが明るくなると考えられます.しかし実際は,スクリーン上では二つのスリットで回折した波が干渉したと考えられる縞模様が観測されました.このことから当時,光は波であるという考え方が主流となりました.

https://commons.wikimedia.org/wiki/File:Ebohr1_IP.svg
光の波動性は,電磁相互作用に関する現象を記述する電磁気学からも示されます.スコットランドの物理学者ジェームズ・クラーク・マクスウェルは,電場と磁場は互いに関連していて波のように進む性質があることを示しました.いわゆる電磁波です.そして,電磁場を記述する基礎方程式であるマクスウェル方程式から,電磁波の進む速さは,光の速さとよく一致することがわかりました.このことから,光は電磁波であると考えられるようになりました.
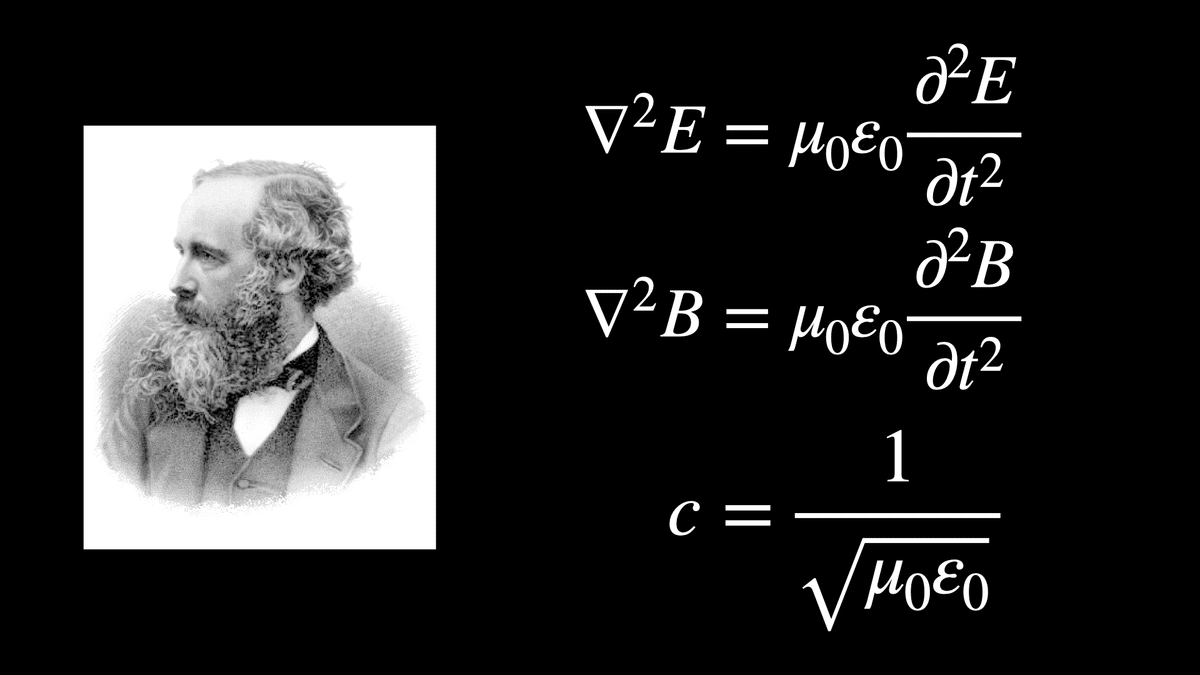
しかし一方で,光の粒子性を示唆する結果も得られるようになります.物体はその温度に応じた色の光を放射する性質があって,黒体放射と呼ばれます.ただ,さまざまな温度を持つ物質からの黒体放射の強度と波長の関係が調べられましたが,当時の物理学をもとにその関係を幅広い波長に渡って説明することはなかなかできませんでした.
1900年,ドイツの物理学者マックス・プランクは,量子仮説と呼ばれる新しい考え方を取り入れることで,この問題が解決できることを示しました.量子仮説というのは,光のエネルギーはとびとびの値しかとることができない,という考え方です.このことは,光のエネルギーは連続的なものではなく,分割できない最小単位(エネルギー素量)があることを示唆しています.
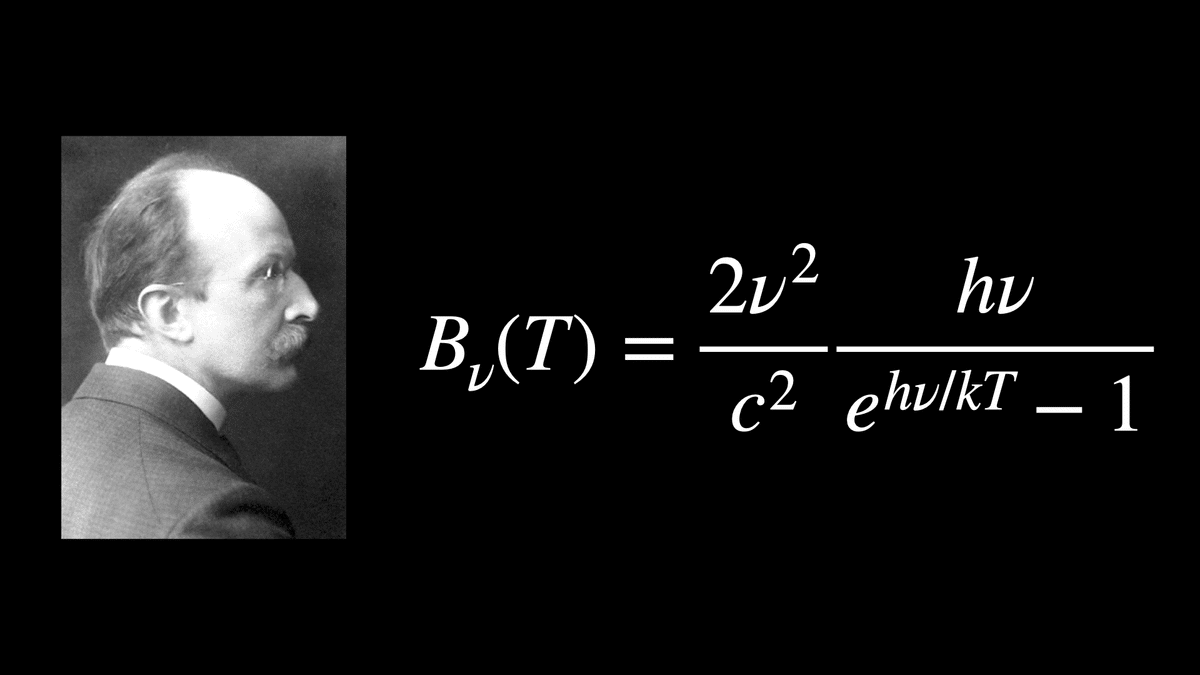
光の粒子性は光電効果の研究からも示されます.光電効果は,物質に光を当てると,光からエネルギーをもらった物質中の電子が放出される現象のことを指します.電子の放出は,ある一定の波長より短い光を当てた場合にしか起こらず,長い波長の光でいくら明るく照射しても電子は放出されません.光が波である場合,明るい光ほど電子に大きなエネルギーを与えられるため,物質から電子が放出されやすくなると考えられます.しかし実際は,そうした波の性質にもとづく予測とは反する結果が得られていました.
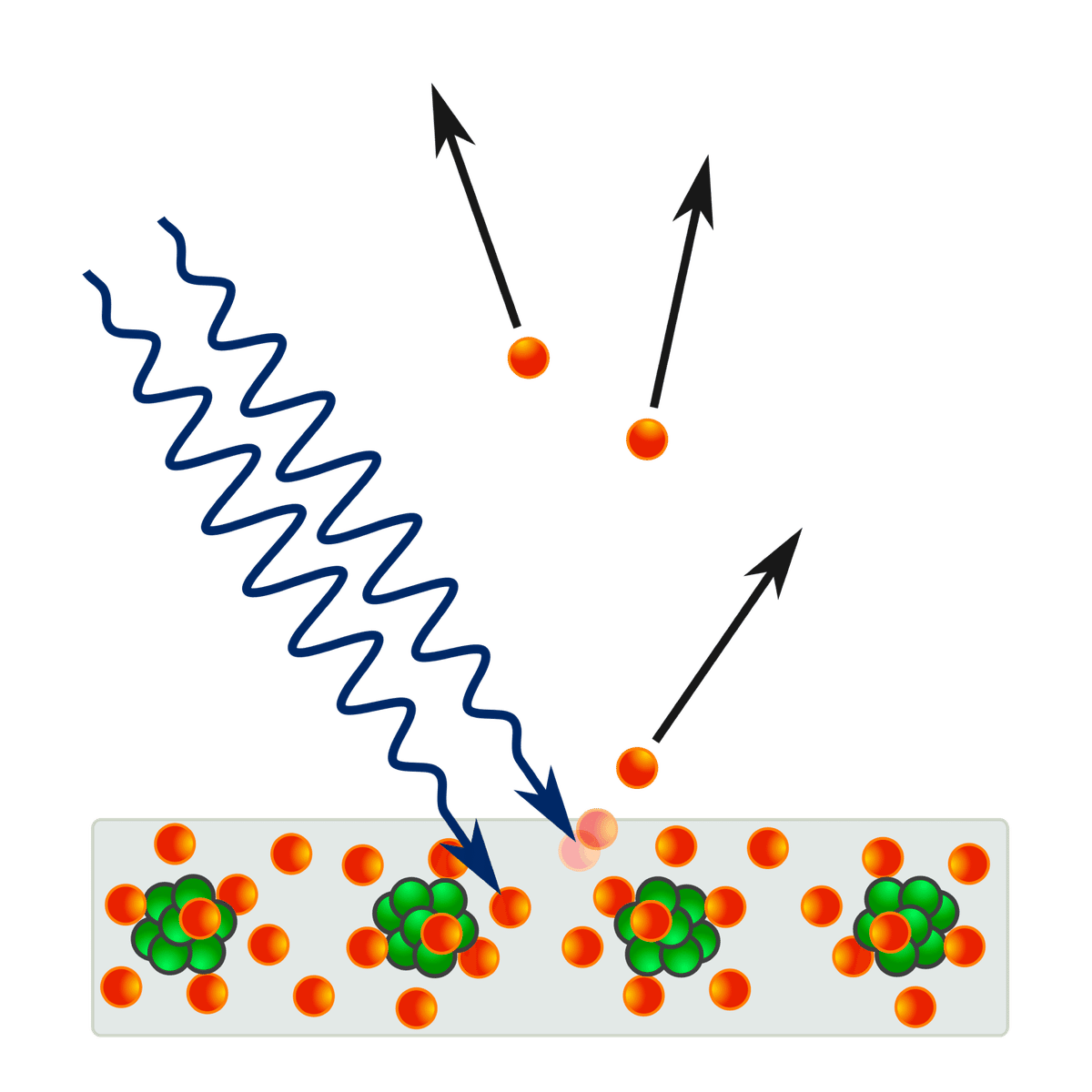
これを解決したのがドイツの物理学者アルベルト・アインシュタインです.アインシュタインは,光が光の粒子(光子)の集合体であると考えました.明るい光は光子の数が多く,逆に暗い光は光子の数が少ないという考え方です.そして,光の波長が短いほど,光子のエネルギーは高いと考えました.そのため,物質に対してある一定の波長より短い光を当てた場合に,物質から電子が放出された,というわけです.

電子の波動性
これらのことから,光は波としての性質と粒子としての性質を併せ持っていると考えることができます.そしてミクロな物質のひとつである電子も同様に波の性質と粒子の性質を併せ持つことが知られています.
電子はレプトンに分類される素粒子のひとつで,陽子や中性子とともにさまざまな原子を構成しています.原子の大まかな構造を明らかにしたのはイギリスの科学者アーネスト・ラザフォードです.ラザフォードはきわめて薄い金箔に対してプラスの電荷を持つアルファ線を照射する実験を行ない,多くのアルファ線がほぼ直進していく中,少数のアルファ線が進路を曲げられたりはね返されたりすることを発見しました.このことは,原子の中央付近のきわめて小さい領域に,プラスの電荷を持つ原子核が存在していることを示唆しています.そして電子はそうしたごく小さい原子核の周囲を回転運動していると考えられるようになりました.
しかし,そうしたラザフォードの原子模型には重大な問題がありました.原子核の周りを電子のような荷電粒子が回転運動すると,荷電粒子は光を放出してエネルギーを失ってしまうという性質があります.そのため,ラザフォードの原子模型では,電子は螺旋状の軌道を描きながら時間とともに原子核へと落ちていくため,原子は安定して存在できないことになってしまいます.

この問題を解消するため,デンマークの物理学者ニールス・ボーアは1913年,ある仮説にもとづく原子模型を提唱します.電子は離散的なエネルギー状態に属していて,それに対応する軌道を運動している電子は光を放出しないという仮説で,ボーアの量子条件と呼ばれます.具体的な表式は角運動量が$${\dfrac{h}{2 \pi}}$$の整数倍のみの値をとることを示していて,角運動量の量子化を表していると解釈できます.

さらに1924年,原子の構造を考える上で重要なアイデアがフランスの物理学者ルイ・ド・ブロイによって発表されます.ミクロな世界では物質粒子も光子と同様に波の性質を持っているという考え方です.運動量$${p}$$の粒子は,プランク定数$${h}$$を運動量で割った波長を持つ波とみなせるというもので,そうした波のことをド・ブロイ波もしくは物質波と呼びます.これはアインシュタインによる光子の考え方に影響を受けたものとされています.光が波動性と粒子性の両方を持つとされるようになった中で,電子などの物質粒子も粒子としての性質だけでなく波の性質も持つと考えたのです.

ボーアの量子条件にド・ブロイ波の式を代入すると,興味深い結果が得られます.電子の運動量が質量と速度の積であることに注意すると,$${2 \pi r}$$すなわち電子軌道の一周の長さは,$${n \lambda}$$すなわち物質波の波長の整数倍に等しいということになります.このことから,電子が存在できる軌道はとびとびであることが示唆されます.
$$
\begin{align*}
m_e v r
&= n \dfrac{h}{2\pi} \\
\to \,\,\,
p r
&= n \dfrac{h}{2\pi} \\
\to \,\,\,
2 \pi r
&= n \dfrac{h}{p} = n \lambda
\end{align*}
$$
各軌道は電子の異なるエネルギー状態に対応していて,外に行くほどそのエネルギーは高くなります.通常,電子はエネルギーが最も低い軌道にいて,その状態は基底状態と呼ばれます.そこにちょうどよいエネルギーを持つ光子が飛んでくると,電子はその光子を吸収することでより高いエネルギー準位へと遷移し,励起状態になります.励起状態にある電子はしばらくするとまた低いエネルギー準位へと遷移します.その際,遷移前後の軌道間のエネルギー差に相当するエネルギーを持つ光子が放出されます.
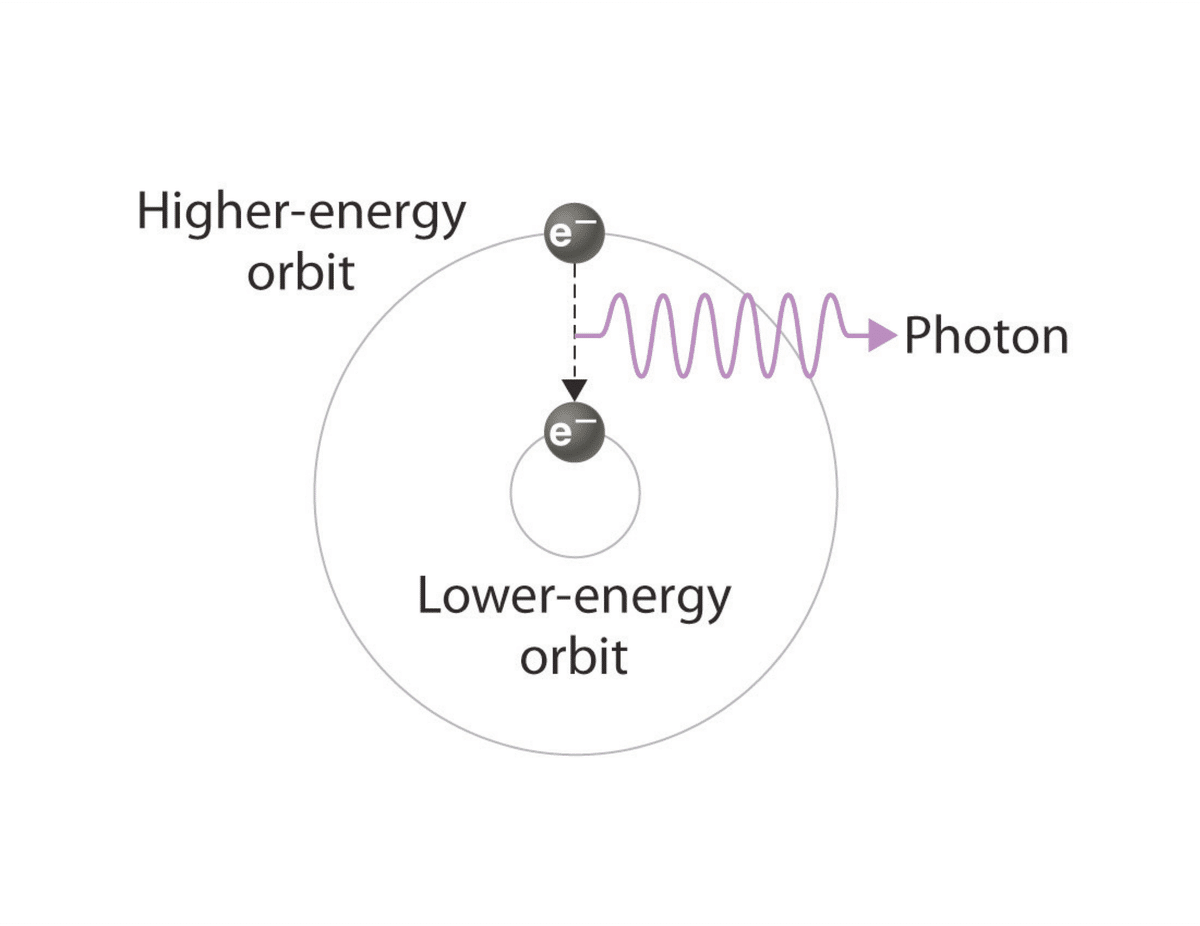
基底状態や励起状態に対応するエネルギーは原子によって決まっているため,軌道間のエネルギー差も決まっています.そのため,各原子は軌道間のエネルギー差とちょうど同じエネルギーを持つ光子を吸収したり放射したりすることになります.たとえば,水素原子が放射する光を観測すると,量子論的な原子模型から予測されるエネルギーとよく一致することが知られています.このことから,電子は波の性質も持つと考えられるようになりました.

状態の重ね合わせ
量子論において私たちの常識と大きく異なるもうひとつの現象は,状態の重ね合わせです.まず日常生活において,中を見ることのできない箱に小さなボールを入れて,適当に箱を振った後で箱の真ん中に仕切りを挿入することを考えます.当然このとき,ボールは箱の中で仕切りで区切られた領域のいずれかに存在しています.
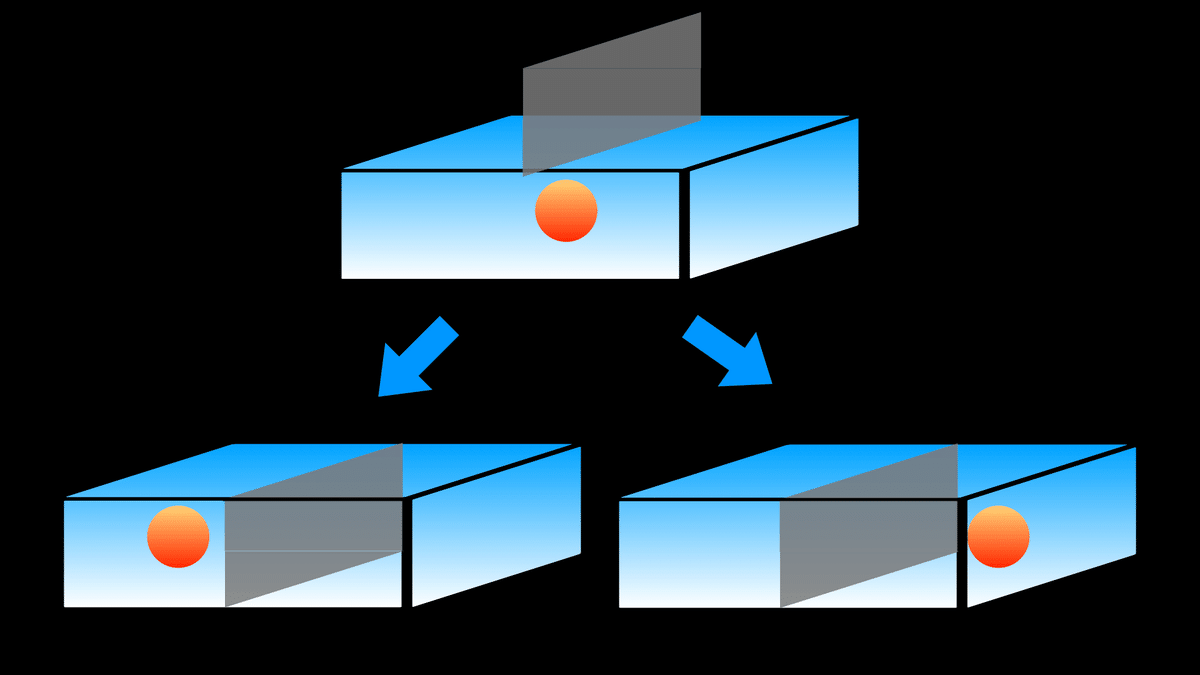
ところが量子論で扱うミクロな世界では状況が変わります.仮想的なとても小さい箱の中に電子を入れることを考えます.電子が箱の中のどこにいるかはわかりません.そして先ほどと同様に,箱に仕切りを挿入します.先ほどの例では,ボールは仕切りで区切られた領域のいずれかに存在していました.しかし電子の場合は,仕切りで区切られた両方の領域に同時に存在していることになるのです.

この現象は,電子が複数個に増えたために生じているのではないことに注意が必要です.電子は観測するまでは仕切りで区切られたそれぞれの領域にいる状態が共存していますが,観測するといずれかの状態に確定します.とても奇妙な性質のように聞こえますが,そのように考えないと説明できない現象が実際に見つかっています.その代表例が二重スリット実験です.
二重スリット実験とコペンハーゲン解釈
ヤングの実験では,位相のそろった光を二つのスリットに通した場合,その先のスクリーンで干渉縞が観測されることを紹介しました.ここでは光ではなく電子を用いることを考えます.電子を1つ打ち出すと,スクリーン上には1点だけ電子が観測された跡が現れます.この結果だけを見ると,電子は粒子として振る舞っているように見えます.

しかし,繰り返し何度も電子を発射していくと,スクリーン上にはしだいに縞模様が現れてきます.もし電子が単に粒子の性質しか持たないのであれば,スクリーン上で電子が観測されるのは,電子の発射元と二つのスリットの延長線上のあたりだけになると期待されます.しかし実際は,スクリーン上では二つのスリットで回折した波が干渉したと考えられる干渉縞が観測されるのです.これは電子の波としての性質が現れたためと考えられます.

量子論では,電子の波は電子の発見確率と関係していると考えます.1926年にドイツの物理学者マックス・ボルンによって提案された考え方で,電子は波として広がって存在していて,電子の波の振幅が高い場所ほど電子の発見確率が高くなるというものです.確率解釈と呼ばれます.
二重スリット実験で打ち出された電子は波として二つのスリットに向かい,それらのスリットを通過して二つの波となります.そしてそれらの波が干渉しながらスクリーンに到達することで,スクリーン上では電子の発見確率の高い場所と低い場所が干渉縞のように交互に生じることになります.電子をひとつ発射するとスクリーンには1点だけ観測点が得られますが,たくさんの電子を発射すると電子の発見確率の高い場所に多くの電子が観測されるようになり,実際に干渉縞が現れる,というわけです.
また,電子の波は,スクリーン上で観測される直前まではスクリーンいっぱいに広がっていますが,スクリーンで観測された瞬間に1点に収縮して粒子として観測されることになります.こうした波の収縮と確率解釈を合わせた考え方は,コペンハーゲン解釈と呼ばれています.コペンハーゲン解釈はさまざまな観測事実と矛盾しないため,量子論において標準的な解釈とされています.ただ,そもそもなぜ波の収縮が起きるのか,収縮前に広がっていた波はどこへ消えたのか,といった根本的な問題は解決されていません.

ミクロな世界の振る舞いをさらによく理解するために,二重スリット実験において,電子がスリットを通過する際に電子を検出できる装置を置いて同じ実験をしてみます.発射された電子は波として二つのスリットを通過することから,両方のスリットで電子が検出されると考えるかもしれません.しかし実際は,いずれかのスリットでしか電子は検出されません.そしてこのとき,興味深いことに繰り返し電子を発射してもスクリーン上に干渉縞は現れません.多数の粒子の発射を想定したときに期待されたように,電子が観測されるのは,電子の発射元と二つのスリットの延長線上のあたりだけになるのです.

https://www.oist.jp/ja/photo/%E4%BA%8C%E9%87%8D%E3%82%B9%E3%83%AA%E3%83%83%E3%83%88%E5%AE%9F%E9%A8%93
コペンハーゲン解釈にもとづくと,スリットに置いた装置で電子が検出されると,電子の波は収縮して粒子として振る舞うようになります.そのため電子はスリットのいずれか一方しか通らないことになり,粒子性を示すようになって干渉縞は消えてしまう,というわけです.

電子の波を数学的に表したものは波動関数と呼ばれます.1926年,オーストリアの物理学者エルヴィン・シュレディンガーは,波動関数の変化を記述する方程式を導きました.シュレディンガー方程式と呼ばれます.この方程式を駆使すれば電子や原子の発見確率を計算することができ,それらの振る舞いを詳しく知ることができます.
$$
\begin{align*}
i\hbar\dfrac{d}{dt}\psi(t)
= \hat H \psi (t)
\end{align*}
$$
不確定性原理
ミクロな世界には,さらに不思議な性質があります.多くの状態が共存しているため,位置と運動量を同時に正確に決めることはできない,というものです.1927年にドイツの物理学者ヴェルナー・ハイゼンベルクにより提唱されたもので,不確定性原理と呼ばれます.

不確定性原理によると,ミクロな粒子の位置の不確かさと運動量の不確かさの積には最小値が存在しているため,位置を正確に決めると運動量の不確かさが大きくなり,運動量を正確に決めると位置の不確かさが大きくなります.電子一つに着目しても未来を正確に予言することは不可能ですから,ラプラスの魔物のように初期条件をすべて知っている存在がいたとしても,その先の未来をすべて予言することはできないことになります.
不確定性原理は,エネルギーと時間の間にも成り立つことが知られています.そのため,ある程度長い時間スケールで見ると粒子のエネルギーをほぼ正確に決めることができますが,きわめて短い時間スケールで見ると粒子のエネルギーは大きな不確定性を持つことになります.
$$
\begin{equation*}
\Delta E \Delta t \geq \dfrac{\hbar}{2}
\end{equation*}
$$
ところで特殊相対性理論から,質量とエネルギーの等価性が示されています.このことは,あるエネルギーをもとにして,それに対応する質量を持つ物質を生成することが可能であることを意味します.実際,粒子加速器ではきわめて高速に加速した粒子を衝突させて,そのときの膨大なエネルギーをもとにさまざまな粒子を生成する実験を行なっています.

エネルギーと時間の間の不確定性関係と,質量とエネルギーの等価性から,真空で粒子の生成と消滅が起きていることが期待されます.真空は量子論的な最低エネルギー状態を表していて,その意味でエネルギーは確定していますが,きわめて短い時間スケールで見ると場所ごとのエネルギーは不確定で揺らいでいます.そして中には非常に高いエネルギーを持つ領域が生じることがあり,そのエネルギーをもとに電子などのミクロな粒子が生成する可能性があります.ただし,長い時間スケールでは不確定性はなくなりますから,真空で生じた粒子は基本的にはすぐに消滅してしまいます.量子論をもとにすると,真空の持つエネルギーのゆらぎによってミクロな粒子が生成しては消滅している,という描像が得られます.
カシミール効果とダークエネルギー
真空のエネルギーの存在は,カシミール効果の実験で確かめられています.カシミール効果は,とても小さい距離を隔てて設置された二枚の平面金属板が真空中で互いに引き合う現象のことです.真空では短い時間スケールで仮想粒子の生成と消滅が起こります.仮想粒子は波の性質を持ちますが,金属板の間の距離がきわめて小さい時,金属板間では量子化された飛び飛びの波長の仮想粒子しか存在できません.それに対して金属板の外側ではそうした波長の制限がないため,仮想粒子が多く存在できます.金属板間と外側での仮想粒子の差が真空のエネルギーの差を生むことで,カシミール効果が起こります.

さらに真空のエネルギーはミクロな世界だけでなく宇宙全体にも影響を及ぼしているかもしれません.Ia型超新星などの観測から,宇宙の膨張史は加速膨張に転じていると考えられていて,宇宙には「反発する重力」として作用する未知のエネルギー成分があると考えられています.いわゆるダークエネルギーです.その正体は解明されていませんが,その候補の一つと考えられているのが真空のエネルギーです.

https://www.nobelprize.org/prizes/physics/2011/summary/
真空のエネルギーは,真空で生成したり消滅したりする仮想粒子のエネルギーすべてを足し合わせたものです.そして,真空のエネルギーは理論的にはまさに反発する重力として作用すると考えられています.ただ,真空のエネルギーを単純に計算すると,観測で得られているダークエネルギーの値より120桁も大きい値になってしまいます.この食い違いの原因は,真空のエネルギーの絶対値を扱うことのできる理論がまだ構築されていないためとされています.
トンネル効果(アルファ崩壊と核融合反応)
不確定性原理で説明される有名な現象がもうひとつあります.ミクロな粒子が一時的に大きなエネルギーを持ち,本来越えられない「壁」を越える現象で,トンネル効果と呼ばれます.

1928年,アメリカの物理学者ジョージ・ガモフは,原子核のアルファ崩壊に量子論を適用し,トンネル効果によってアルファ粒子が原子核周りのポテンシャルの壁を透過することで起きる現象であることを示しました.
アルファ粒子は陽子二個と中性子二個からなるプラスの電荷を持つ粒子です.原子核中ではプラスの電荷を持つ陽子がきわめて小さい領域に存在しているため,陽子同士は互いに電気の力で反発しています.しかし,原子核内のようなきわめて小さいスケールでは,それにも増して強力な強い核力がはたらくため,たくさんの陽子が集まった状態で原子核を形成することができます.
通常,原子核中のアルファ粒子は強い核力によって結合していて,エネルギーの山に囲まれたくぼ地にいるような状態にあります.ただ,不確定性原理によると,ミクロな粒子は短い時間スケールでは大きなエネルギーを持つ可能性があります.そして,エネルギーの山を越えるのに十分なエネルギーを持ってポテンシャルの壁をすり抜け,強い核力の及ばないところまで飛び出すことがあります.すると,原子核とアルファ粒子はともにプラスの電荷を持っているため互いに反発し,そのままアルファ粒子は原子核から放出されることになります.これがアルファ崩壊のメカニズムです.

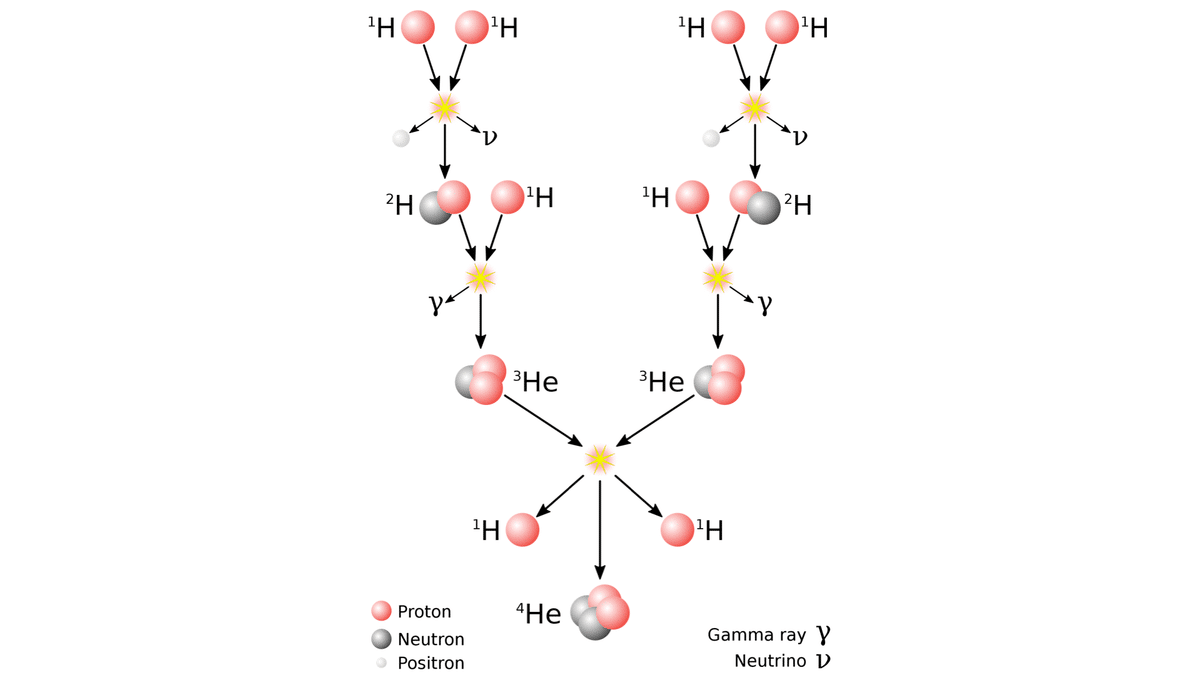
また,恒星内部の核融合反応もトンネル効果のおかげで起きていると考えられています.恒星の内部では陽子同士が衝突することで核融合反応が起きていますが,陽子はプラスの電荷を持つため,二つの陽子がクーロン障壁を越えて反応するためにはきわめて高速で近づく必要があり,そのためには温度が10の10乗ケルビンを越えるきわめて高温である必要があります.

しかし太陽の場合,中心の温度は10の7乗ケルビン程度と見積もられているため,核融合反応を起こすには温度が十分高くないことになってしまいます.そこで適用されるのがトンネル効果です.トンネル効果のおかげで,陽子は十分な速さを持っていなくても,互いのクーロン障壁をすり抜けて衝突することが可能となるわけです.
今回は物理学で重要な理論のひとつである量子論について,波と粒子の二重性や状態の重ね合わせ,不確定性原理といった,日常生活にもとづく常識では理解することの難しい現象に着目して紹介してきました.実はそうした不思議な性質を示す量子論は,私たちの生活に大きく貢献してくれています.例えば金属・半導体・絶縁体といった固体の性質や,化学反応,超電導などの仕組みは量子論によって理解することができます.さらに,超高速計算を可能にする量子コンピュータや,量子もつれを使った量子テレポーテーションなど,これからの社会に大きく貢献する可能性のある技術の研究も進められています.量子論にもとづいた新しい技術がよりよい未来をもたらしてくれることに期待したいです.
参考文献
東京大学の先生伝授 文系のためのめっちゃやさしい量子論
https://amzn.to/3Itwvkp
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
