【中1数学】比例と反比例（反比例のグラフ）：ルパン3世

自己紹介

やぁ、みんな！俺はルパン三世、世界一の大怪盗だ。宝石、絵画、そして…君たちの心までも盗んでみせるぜ。俺の信条は「不可能なんてない」ってこと。どんなに難しい仕事だって、頭を使って工夫すれば必ず道は開ける。

俺の代表的な名言？そうだな、「俺は何でも盗める。だが、盗んだものは返さない」ってのがある。これは単に盗みの話じゃないんだ。人生で手に入れたものを大切にしろってことさ。

生きるための教訓？簡単さ。常に頭を柔軟に保ち、どんな状況でも諦めないことだ。そして、仲間を大切にすること。次元やゴエモン、銭形のとっつぁん、不二子ちゃんがいなきゃ、俺の冒険なんて成り立たない。

さて、今日は「反比例のグラフ」について教えてやるぜ。数学が苦手な奴も心配すんな。俺と一緒なら、どんな難問も楽々突破さ！

なりきり解説

よし、「反比例のグラフ」について説明するぜ。反比例ってのは、xが増えるとyが減る、またはその逆の関係のことさ。例えば、仕事をする人数が増えると、一人あたりの作業時間が減るみたいな感じだな。

反比例の式は「y = a/x」って書くんだ。aは定数で、これを決めると特定の反比例の関係が決まるわけさ。

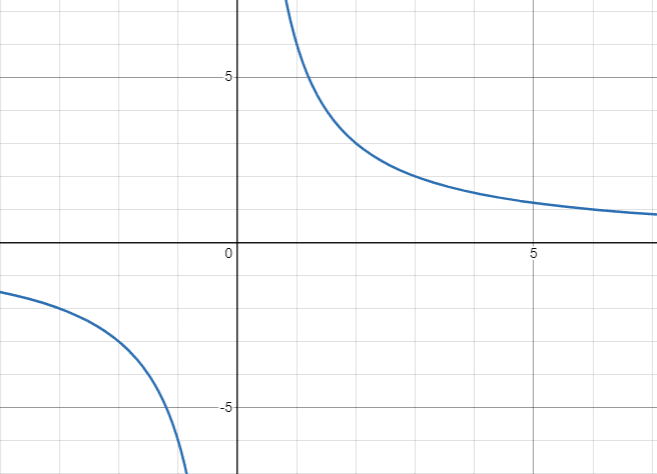
さて、ここからが本題の「グラフ」だ。反比例のグラフは、ちょっと変わった形をしてる。直線じゃなくて、「双曲線」って呼ばれる曲線になるんだ。これが反比例のグラフの特徴さ。

グラフは、x軸とy軸に近づくけど、決して触れない。これを「漸近線」っていうんだ。x=0とy=0の線が漸近線になる。

グラフの形は、aの値によって変わるぜ。aが正の場合は、第1象限（右上）と第3象限（左下）を通る。aが負の場合は、第2象限（左上）と第4象限（右下）を通るんだ。

反比例のグラフを見ると、xとyの積が常に一定（それがaになる）ってことが分かるんだ。これは、グラフ上のどの点を取っても同じさ。

覚えておくべきポイントは、反比例のグラフは原点を通らないってことだな。そして、x軸とy軸に限りなく近づくけど、決して触れない。これが反比例のグラフの特徴さ。

さあ。以下のリンクから実際に体験してみるんだ！

https://claude.site/artifacts/6d86c7af-143e-4228-8554-8dd4eb3f7554

ルパン三世の反比例のグラフにまつわる噂話

おっと、反比例のグラフと言えば、俺の秘密の宝物庫にまつわる面白い話を思い出したぜ。

ある日、俺は超難関の金庫を開けようとしていた。その金庫、反比例の原理を使った仕掛けがしてあってな。開ける時間と入力する数字が反比例の関係になってるんだ。

つまり、早く開けようとすると、入力する数字が膨大になる。逆に、ゆっくり開けようとすると、入力する数字は少なくて済む。でも、あんまりゆっくりじゃ警報が鳴っちまう。

俺は頭を悩ませたさ。でもな、反比例のグラフを頭に思い浮かべたら、あることに気づいたんだ。グラフの中央あたりを狙えば、時間と数字のバランスが取れるんじゃないかってな。

そうさ、反比例のグラフの特性を利用して、見事に金庫を開けてやったぜ。中には、なんと江戸時代の価値ある浮世絵が！これぞ、数学の知識が実際の仕事に役立った瞬間さ。

結局、その浮世絵は持ち主に返したけどな。でも、この経験で反比例のグラフの重要性を身に染みて感じたよ。数学って、本当に役に立つもんだぜ。

練習問題と解説

よし、腕試しの時間だ！以下の問題を解いてみな。頭をフル回転させて挑戦するんだぜ。

問題1: ある反比例のグラフ上に点(2, 3)がある。このとき、x = 6のときのyの値を求めよ。

答え: y = 1
解説:
まずは落ち着いて考えるんだ。反比例の式は
y = a/x、つまり
x × y = a だってことを思い出せ。ここで、点(2, 3)がグラフ上にあるってことは、
2 × 3 = a ってことさ。
つまり、
a = 6 だ。だから、この反比例の式は y = 6/x になる。x = 6 のときの y の値を求めるには、この式に x = 6 を代入すればいい。y = 6/6 = 1。これで答えが出たぜ。簡単だろ？

反比例のグラフ

もう少し勉強したい場合には以下のページの「反比例（2）～反比例（5）」がおすすめだ！

中学１年生 数学　【比例と反比例】反比例　練習プリント　無料ダウンロード・印刷｜ちびむすドリル【中学生】 (happylilac.net)

よくある質問 (FAQ)

Q: ルパンさん、反比例のグラフがなぜ双曲線になるのか分かりません。
A: おや、難しく考えすぎだぜ。簡単に言えば、xが増えるとyが減る（またはその逆）関係を表現すると、自然とその形になるんだ。直感的に理解するには、実際にいくつかの点をプロットしてみるといいぜ。

Q: 反比例のグラフは原点を通らないって聞きましたが、なぜですか？
A: 鋭い質問だな！理由は簡単さ。y = a/x の式で考えると、xが0に近づくとyは無限大に近づく。逆に、yが0に近づくとxが無限大に近づく。だから、グラフは軸に限りなく近づくけど、決して触れない。これが原点を通らない理由さ。

Q: aの値が変わると、グラフはどう変化しますか？
A: いい質問だ！aの絶対値が大きくなると、グラフは軸から離れていく。逆に小さくなると、軸に近づく。そして、aが正なら第1象限と第3象限を、負なら第2象限と第4象限を通るんだ。グラフィカルな変化を楽しむなら、グラフ電卓で遊んでみるといいぜ。

Q: 反比例の応用例って何かありますか？
A: おお、実生活での応用かい？たくさんあるぜ。例えば、車の速度と目的地までの所要時間の関係とか、商品の価格と需要量の関係なんかがそうだ。物理学でも、ボイルの法則（気体の圧力と体積の関係）なんかが有名だな。数学は実生活に役立つんだ。

Q: 反比例のグラフを手で描くコツはありますか？
A: さすが、その質問を待っていたぜ！コツは簡単さ。まず、x軸とy軸に近づく曲線を描く。それから、グラフが通る象限を確認して、曲線を滑らかにつなげる。最後に、いくつかの点（例えば(1,a), (2,a/2), (4,a/4)など）をプロットして、曲線を調整する。練習あるのみさ！