
プロデューサーと篠澤広が「CHAOS」について話すようです
*篠澤広の親愛度1~10話のネタバレが含まれています。また独自の設定を追加している部分があります。
*非線形物理学のカオス理論について、カオスの定義とローレンツ・アトラクターの紹介を目標にした怪文書です。物理に詳しくない人でもわかるように、極力数式を出さないようにして、定性的な話に留めています。誤字脱字含めて、何か間違ってる部分があったら教えてください。
*(DDRにおけるCHAOSの話はほとんど)ないです。
*この記事はKBD合同アドベントカレンダー企画によるものです。他の記事も見てみてねー
プロローグ
P「~♪」
プロデューサーとの会議をするために教室に入ると、先に教室にいたプロデューサーがリズムに乗りながら音楽を聴いていた。
彼があんなにノリノリなところは、いつもの冷酷な扱いからは想像できなくて、おもしろい。
…….それにしても、リズムが変。プロデューサー、リズム感ないのかな?
広「(そうだ。)」
気づかれないように、こっそり背後に忍び寄る。
広「わっ!」
P「うわっ!……なんだ、篠澤さんですか。」
広「ふふ、プロデューサーが驚いてるところ、初めて見た。」
広「いま、何聞いてたの?」
P「えっと……これは説明が難しいのですが」
話を遮るようにして、プロデューサーが外したイヤホンを耳につける。
ジャカジャッ ジャン! ジャ カッ ジャ カッ ジャ ジャカハイ!
これは……何だろう。いつも彼は私の理解を超えてきてくれておもしろい。
広「……なるほど。Dance Dance Revolutionに収録されている、CHAOSのExpert譜面を覚えるための音MADだったんだ。」
広「曲名を聞いたら、プロデューサーが不規則なリズムに乗っていたのも納得。」
P「そういえば篠澤さんの専攻は物理でしたよね。物理にもCHAOSという用語は登場するのですか?」
広「それほど詳しくはないけど、聞いたことはある。」
広「プロデューサー、わたしがCHAOSの講義、してあげようか?」
多分、「講義する体力があるならアイドルのレッスンをしてください。」なんて言われるけど、冗談のつもりで訊いてみる。
P「せっかくなので、素人でもわかるようにお願いします。」
……意外。この前わたしの経歴をアイドル活動には使わない、って話をしたはず。わたしのアイドルとしての才能を見限って、高学歴アイドルとして売り出すことにしたのかな。
広「それじゃあ、講義をはじめるよ。」
第一章~相空間とトラジェクトリー~
わたしは最初に質問を投げかける。
広「プロデューサー、フラクタル次元って言葉、聞いたことある?」
P「いや、聞いたことがないです。」
広「じゃあ、アトラクターは?」
P「英単語としては聞いた事がありますが、物理用語としての意味はわからないです。」
広「……うーん、相空間くらいは、きいたことある?」
P「……いえ。」
たしかに、通常のカリキュラムでは相空間あたりの話は2年で触れる話題だったかも。物理専攻でもない1年の彼がわからないのは至極当然といえる。
広「ふふ、教え甲斐がありそう。」
P「そんなニヤニヤした顔で見つめないでください……」
広「じゃあ、まずは相空間について、話していくよ。」
そう言って、わたしは黒板に簡単な図を書いていく。
……
広「プロデューサー、垂直投げ上げ運動って、覚えてる?」
P「それは覚えています。物体を真上に投げると、最初は上向きに動きますが、重力によって徐々に減速していき、ある地点で下向きに動くように切り替わる、という運動だと記憶しています。」
広「その通り。この物体のトラジェクトリー(軌跡)を座標平面上に描くと、こうなるよね。」

高校で見たことある人も多いはず
P「すみません、大まかなニュアンスは把握しているのですが、一応座標平面とは何か説明してくれませんか?」
広「うん、いいよ。座標平面とは、平面上の物体について、x軸、y軸への垂線を引いた時、軸との交点の値で物体の位置を1つに特定できる平面のことだね。今回の例だと、物体は高さ方向にしか動かないから、x軸だけで十分。」
広「言い換えると、座標平面は物体の「位置のみ」を示した平面、ということ。」
……
広「これに対して、相平面は位置に加えて速度(厳密には運動量)の情報を新しい成分として付け加えた平面のことだよ。相空間はさらに他の状態変数を付け加えたもの。」
P「……?いきなりよく分からなくなりました。」
広「さっきの例に戻ってみよう。」
広「垂直投げ上げ運動について、物体のトラジェクトリーは座標平面上に描くと図1.1の通りだった。」
広「プロデューサー、さっき物体の速度は下向きに増加していくって言ってたよね。」
広「物体の位置を横軸、速度を縦軸として、今度は相平面上に物体のトラジェクトリーを描いてみる。」

(凸凹ミスってるかも)
P「なるほど。初速度は正であるから縦軸の正の切片からスタートする。そして時間が経つにつれ速度は負の方向に増加するから、下方向にトラジェクトリーが描かれているのですね。」
広「その理解で合ってる。さすがプロデューサー、ものわかりがいい。」
……
広「ここで1つ、重要なトラジェクトリーの性質を紹介するよ。」
広「その性質は、相空間上でトラジェクトリーが交わることは決してないということ。」
P「そうなんですか?座標平面しか知らない身としては、交わっても特に矛盾がないように思いますが…」
広「たしかに、座標平面上ではトラジェクトリーが交わっても問題ない。」
広「でも、例えばある位置、ある速度で斜面を下っているボールが重力を無視して減速したり、逆走し始めたら変、だよね。」
広「直感的な理由は、そんなイメージ。」

この系では(x0, y0)上の物体が赤の軌道に移ることはできない
P「まだ上手く噛み砕けてはいませんが、納得はできました。」
広「相空間についての話は、とりあえずこんなところ。これからは基本的に相空間を用いて議論するよ。」
広「つぎに、アトラクターの話をしていく。プロデューサー、大変そうだけど、頑張ってついてきて。」
P「篠澤さん、自他共に追い込むのが好きなので自分の得意分野に関してはスパルタ教師ですね……」
……
わたしは、大学で経験したことについては、すべてつまらないものだと考えている。プロデューサーは物理専攻でもないのに、どうしてこんなつまらない講義を受ける気になったんだろう。本当に、見限られちゃったのかな……。
第二章~「変じゃない」アトラクター~
第一節 アトラクターの定義
広「じゃあ、次はアトラクターの話をする、よ。」
広「プロデューサー、英単語としてのアトラクターってどんな意味だったか、おぼえてる?」
P「確か、引き寄せるもの、みたいな意味だったはずです。」
広「そう。物理においても、ニュアンスはおおむねそんな感じ。」
広「とりあえず、アトラクターの厳密な定義を引用しておく。」
多分わからないだろうなと思い、ちょっとわくわくしながら定義を書いていく。
より正確には、アトラクターは次の性質を満たす閉集合Aとして定義される。
(1)Aは不変集合(invariant set)である。すなわち、A内から出発するどのような軌道x(t)もその後ずっと常にAに留まる。
(2)Aは初期条件からなる開集合を吸引する。すなわちx(0)∈Uであるならば、その後のx(t)とAとの距離がt→∞で0に漸近するようなAを含む開集合Uが存在する。このことは、Aがその十分近くから出発するすべての軌道を吸引することを意味している。そのようなUのうち最大のものをAの吸引領域(basin of attraction)とよぶ。
(3)Aは極小集合(minimal set)となっている。すなわちAのどのような真部分集合も以上の条件(1)および(2)を満たすことはない。
P「申し訳ないのですが、書いてあることが何にもわかりません。」
広「ふふ、流石のプロデューサーも、くるしそう。」
広「これから具体例でわかりやすく説明するから、安心して。」

広「上の図のような相平面上のグラフについて、考えてみる。」
広「このグラフは、3つの領域に分けられるね。」
P「中心の真横の部分に対して、左右に突起が出来ていますね。」
広「えぐざくとりー。中央の部分がアトラクター、突起が吸引領域、突起の外が吸引領域外に対応してる。」
……
広「まず、(1)について考えてみる。簡単に言い換えると、中央からスタートした物体は決して底から斜面に出てこない、ということ。」
P「何となく言いたいことはわかりました。しかし、物体に十分な初速度を加えれば坂を登れそうな気がしますがどうなのでしょう。」
広「プロデューサー、今は相平面について議論してることを忘れてる。図2.1.1において、縦軸は「高さ」じゃなくて「速度」だよ。」
P「そういえばそうでした。つまり、斜面上では物体は底に向かう方向の速度を常に持つため、逆に底から斜面に移動することはできない、ということですね。」
広「おふこーす。(1)については理解できたみたい。」
……
広「そしたら、次は(2)について考えてみる。文章は1番長いけど、言ってることは簡単。要するに、突起からスタートした物体はいつか必ず中央に着く、という意味だね。」
P「確かにこれは直感的にも分かりやすいです。ちなみに(3)はどういう意味ですか?」
広「うーん……一応説明すると、中央を一部切り取ったものだけを考えてもアトラクターとはならない、という意味。」
広「でも、(3)はあまり重要じゃないから理解できなくても、大丈夫。」
P「わかりました。とりあえずこれで、アトラクターの定義については概ね理解できたと思います。」
第二節 「変じゃない」アトラクターの種類
広「じゃあ、次は「変じゃない」アトラクターの種類について紹介する、よ。」
P「すみません。「変じゃない」とはどういう意味かちょっと気になります。」
広「プロデューサー、意欲的で優秀な学生だね。でも、今説明するとかえって難しくなるから、ちょっとがまん。」
広「まずは、1点からなるアトラクターから始めよう。」

広「上の図は、座標平面上について考えた落とし穴を示してる。物体と落とし穴の斜面の間には摩擦があると仮定した。ちなみに、x軸は落とし穴の斜面に沿って設定してあることに注意。」
広「この落とし穴の斜面上に物体を置くと、どんな運動をすると思う?」
P「物体が斜面を下って、その勢いで対面の斜面を登ると思います。摩擦があることを考慮すると、その運動を繰り返しながら、いつかは落とし穴の底で止まるのではないのでしょうか。」
広「うん、その通り。じゃあ、物体のトラジェクトリーを相平面上に、描いてみて。」
P「篠澤さん、初学者に対してスパルタすぎませんか……えっと……恐らく、こうだと思います。」

原点に向かって収束していることが分かる

広「すごい。プロデューサーが、正しいトラジェクトリーを描けると思わなかった。物理の才能もありそう。」
P「解けないと思ってる問題を出さないでください……ところで、これが1点からなるアトラクターなのですか?」
広「うん。トラジェクトリーがある1点に向かって吸い込まれているから、そう呼ばれているよ。」
……
広「じゃあ次は、リミットサイクルについて説明する。」
P「リミットサイクル?サイクルとついているので、物体が回っているのでしょうか。」
広「まちがってはない。でも、回るのは相平面上での話。」

(これ摩擦強すぎると止まっちゃうから、十分風が強いと考えてください。)
広「さっきの落とし穴について、考えてみよう。でも、今度は物体に対して3箇所から風を送ることにした。」
広「物体が風から受ける力は、近い程強く、遠いほど弱くなるよ。」
広「この場合、相平面上のトラジェクトリーはどうなると思う?ヒントは、物体は最終的に同じ運動を繰り返す。」
P「最終的には、物体が対面の斜面を登って、帰ってきたら元の状態になるループを繰り返すから……これで合っていますか?」


広「正解。トラジェクトリーが最後には1つの楕円となって、ぐるぐるとまわってるね。」
広「このように、トラジェクトリーが1つのループ上で回りながら安定するアトラクターのことを、リミットサイクルと呼ぶよ。」
広「実は、1点からなるアトラクターが存在しない相平面上には、必ずリミットサイクルが存在するという定理が存在する。(ポアンカレ-ベンディクソンの定理)」
広「この定理は3次元以上の空間では成立しないんだけど、この事実がCHAOSの発生に関係しているよ。」
P「ようやく、CHAOSという言葉が出てきましたね……」
広「とりあえず、物体がずっとぐるぐる回るようなアトラクターもある、ということを知っておけば、大丈夫。」
……
広「さいごに、トーラスについて確認しよう。」
広「プロデューサー、角速度って言葉、聞いたことある?」
P「角速度は、高校で聞いたことがあるかもしれないです。」
広「わかりやすくいうと、物体がどのくらい早く円運動を1周するかのパラメーターのこと。」
広「さっき考えたリミットサイクル上では、物体がある1つの固有の角速度をもってループしていたといえる、よね。」
P「なんとなくですが、リミットサイクル上の運動を円運動と見なせば、そんな気がします。」
広「1つの角速度で物体を動かすアトラクターがあるなら、回転する方向が異なる、複数の角速度で物体を動かすアトラクターも存在しそう。そんな発想で考案されたアトラクターが、トーラスだよ。」
P「複数の角速度……?どんなアトラクターかちょっと想像がつきません。」
広「プロデューサーの感想は正しい。実際に、普通の空間上では角速度の種類が3つ以上のトーラスは図示できない。」
P「図示できないアトラクター、いよいよ抽象的な世界になってきましたね。」
広「ちなみに、角速度が2つのトーラスはドーナツみたいな形になる。」

そういえば弐寺にドーナツホールが収録されたらしい(!?)

広「これで「変じゃない」アトラクターの紹介は終わり。」
……
広「ようやく、「変じゃない」とはどういうことか説明するときがきたね。」
広「物体はリミットサイクル・トーラス上では必ず周期的な運動をする、つまり、「変じゃない」アトラクター上の物体は同じ動きをループすることが証明されている。これが、「変じゃない」の意味だよ。」
広「ちなみに、この証明は最初の方で話したトラジェクトリーは交わらないという性質を使うとできる。」
広「……プロデューサー。険しい顔になってるけど、大丈夫?」
P「篠澤さん、そろそろ休憩をはさみませんか?脳がオーバーヒート寸前です。」
広「うん。そうしよう。おやつは、ドーナツにする?」

……
プロデューサーから休ませてくれなんて、いつものレッスンでは絶対に聞けないからとても新鮮。
……さっきから、こころがもやもやする。なんでだろう。
彼の手腕なら、わたしを高学歴アイドルとして売り込み、成功させるのは容易だと思う。
でも、わたしはそんなことを望んでいない、人気アイドルを目指す過程を楽しんでいることを彼は理解していると思ってた。杞憂だと思うけど、このまま講義を進めてしまったら、「わたしにとって楽しい」学園生活が終わってしまいそうで、少し怖い。
どうして講義を受けようと思ったのか、講義を中断する気はないか、これらの疑問を直接訊き、真実を確定させる勇気はわたしにはない。
どうすればよいかわからず、ただドーナツを食べることしかできなかった……
第三章~「変な」アトラクターから生まれる、CHAOS~
第一節 CHAOSを発見するための道具
不安を悟られないよう、できるだけ自然な形で声をかける。
広「……ふぅ。そろそろ、講義を再開する?」
P「だいぶ頭の中が整理されたので、再開できそうです。」
広「わかった。それじゃあ、いよいよCHAOSの話に入るよ。」
広「だけど、その前にCHAOSを発見するための道具を準備しないといけない。」
P「確かに次元が大きく、図示できないアトラクターを考えるのなら、間接的に観測する道具が必要そうですね。」
広「それはちょっと違うかも。詳しくは触れないけど、どれだけ高次元なアトラクターであっても、それが整数ならばCHAOS的な運動はしないことが分かっている。」
広「むしろ、わたしたちが観測したいのは、次元が整数でない、フラクタル次元で表現されるアトラクター。ただ、説明するのがちょっと難しいから、今回はあまり深入りはしない。」
P「次元が整数ではない、ですか。哲学的な話ですね。」
広「プロデューサー、怖がる必要はありませんよ。わたしがひとつずつ、丁寧に教えていきます。」


……
広「まずは、トラジェクトリーX(t)に対して、自己相関関数C(τ)という、τについての関数を定義する。[2]によると、関数の形はこう表される。」

P「トラジェクトリー同士を掛けたものをある時間の区間で積分してることはわかるのですが、この計算で何が求まるのでしょうか。」
広「この計算をすると、時刻tとt+τの間で、トラジェクトリーに相関関係があるかどうかがわかる。」
広「積分の計算結果が大きいほど、トラジェクトリーに相関関係が強くなる。その場合は、相関関係を調べることで、過去の動き方からトラジェクトリーの動き方が予測できるということだね。」
広「一方で、計算結果が0に近くなった場合は、トラジェクトリーが過去の動き方から予測できない運動をしているといえる。」
広「過去の動きから予測ができない。CHAOSの本当の面白さは、ここから始まります。」
P「なるほど。トラジェクトリーに対して自己相関関数を用いれば、その物体の運動が過去の運動から予測可能か分かるんですね。」
広「その通り。さらに、自己相関関数の考察を進めていくよ。」
……
広「自己相関関数に逆フーリエ変換という操作を施すと、パワースペクトルというスペクトル図が得られる。」
P「スペクトル図って確か、横軸が周波数、縦軸が強さ(振幅の二乗)のグラフのことでしたよね。」
P「もしかして、リミットサイクル・トーラス上のトラジェクトリーのパワースペクトルを求めると、アトラクター上の物体が持つ周波数が求まるということですか?」
広「まさにそう。実際に求めてみると、下の図のようにアトラクター上を動く物体が持つ周波数のところだけがとんがってることがわかる。」
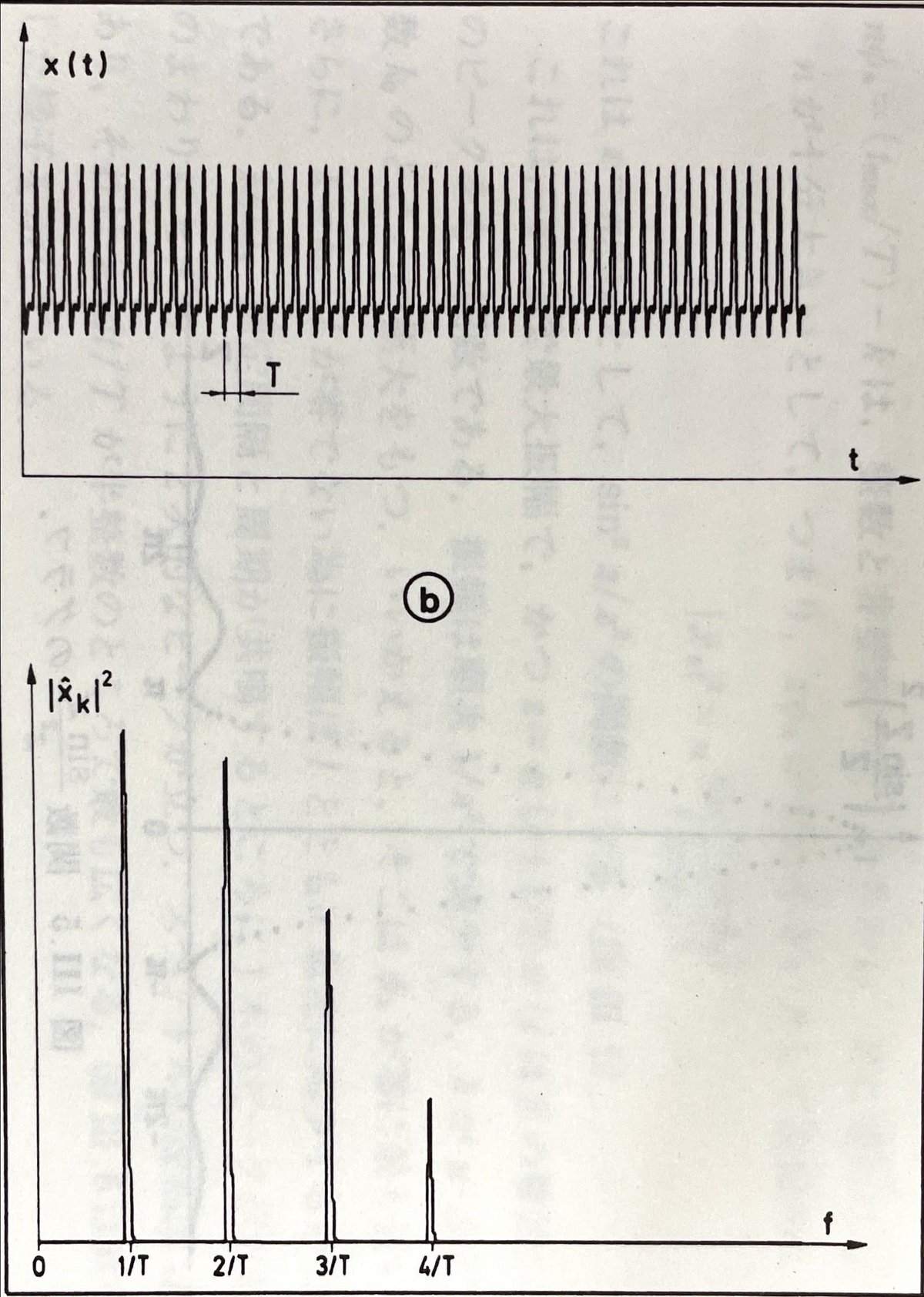
[2]p47より引用
第二節 (やっと)CHAOSの定義(諸説あり)
広「じゃあ、今度はτが大きくなるにつれ0に近づく自己相関関数を取るようなトラジェクトリーのパワースペクトルを求めてみるよ。」
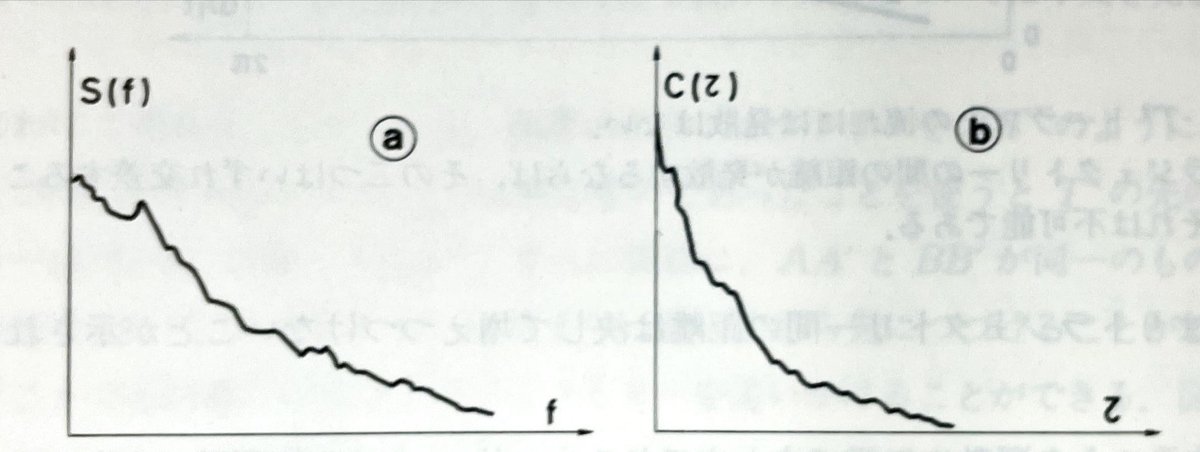
[2]p108より引用
P「パワースペクトルがとんがっている形とは異なり、徐々に減少する形になっていますね。」
広「プロデューサーがbeatmaniaやってるときみたい。」

P「このパワースペクトルに対応する運動は……。あれ、これどうなるんですか?」
広「ようやく、CHAOSのお出ましだね。」
~CHAOSお出ましシリーズ~




ここのCHAOSってゲーム内で重要な曲なのかな

……
広「このように、あるアトラクター上のトラジェクトリーをパワースペクトルで解析したとき、特別強調された周波数をもたないようなアトラクターのことを、ストレンジ・アトラクターと呼んでいる。」
広「そして、ストレンジ・アトラクター上での物体の動きを一般にCHAOSと呼ぶようになった、よ。」
広「CHAOSの定義は人によるから、あくまでこの定義は[1]によるものということは留意しておいて。」
P「「変じゃない」アトラクター上の物体は周期的な運動をすると言っていましたが、ストレンジ・アトラクター上では違う動きをするのですか?」
広「うん。ストレンジ・アトラクター上の物体の動きは非周期的で、微小な初期条件の違いでその後の運動が大きく変わる性質を持っているよ。」
広「簡単に言うと、スタート位置を少しずらしただけでその後の運動が全く異なるものになるということ。」
第三節 バタフライエフェクトと蝶のようなアトラクター
P「すみません、振り出しに戻るような質問をしてもよろしいですか……?」
広「もちろん。物理は基礎を繰り返し振り返ることが大切。」
P「まず確認しておきたいのですが、ストレンジ・アトラクター上でも初期条件が分かっていれば、そのトラジェクトリーは方程式を解いて求めることができるのですよね?」
広「そう。ストレンジ・アトラクターの特徴はあくまで初期条件の違いによって運動が大きく変わることであって、初期条件に対してトラジェクトリー自体は一対一で確定する。つまり、初期条件さえ正確に分かっていればストレンジ・アトラクター上の運動も予測することは可能だよ。」
P「それならば、わざわざ普通の運動とCHAOSとしての運動を区別する意味ってあるのでしょうか……?どちらも初期条件から一つのトラジェクトリーが確定するという点では変わらないと思うのですが……」
……
広「なるほど、確かに初期条件を一切の誤差なく設定できるなら、CHAOSとして区別する必要はないかもしれない。」
広「でも、現実に起きている現象を一切の誤差なく測定し、初期状態を決定するのは無理。それはコンピュータ上で行われる仮想的な実験でも同じ。」
広「下のグラフを見れば、CHAOSの初期値に対する敏感性がわかりやすいかも。」

P「確かに、ほんの少し最初の値を変えただけでその後の運動がバラバラになっています。」
P「しかし、逆に考えると最初の数秒間は多少の誤差があってもほぼ正確に予測できていそうですね。」
P「技術の発展により測定誤差を小さくしていけば、欲しい未来までの運動は予測できそうじゃないですか?」
広「……うーん、測定誤差を小さくする方法だと、あんまり効果がなさそう。[1]p.p351-352によると、測定誤差を数百万分の一にしても予測できる時間は約2.5倍にしかならない。」
広「分子レベルまで誤差を小さくできたとしても、それ以上は不確定性原理より位置を完璧に特定するのは不可能。」
広「このような理由で、実質的に運動を十分な未来まで予測することが不可能な運動のことをCHAOSと呼んで区別するようになった、よ。」
……
広「例えば、天気の移り変わりはCHAOS現象の一例として挙げられる。」
広「気温・湿度・気圧などのパラメーターがちょっと変わるだけで天気が大きく変わるから、今の技術でも予報が外れることがまだまだ多い。」
P「CHAOS現象の具体例が全く思い浮かびませんでしたが、意外と身近なところで起きていたんですね。」
……
広「そういえば、プロデューサーはバタフライエフェクトって言葉聞いたことある?」
P「それは聞いたことがあります。時々映画などでもテーマになっていた気がします。」
広「バタフライエフェクトは気象学者のエドワード・ローレンツによる『Predictability: Does the Flap of a Butterfly's Wings in Brazil Set Off a Tornado in Texas?』というタイトルの講演が由来になっている。」
広「テキサスでのトルネードがブラジルでの蝶の羽ばたきのようにささやかな現象で引き起こされたとして、果たしてわたし達には蝶の羽ばたきが原因であることを特定できるのか。CHAOSの本質がよくわかる、俊逸な例えだね。」
……
広「せっかくだから、ローレンツが発見した最初のストレンジ・アトラクター、『ローレンツ・アトラクター』を見てみよう。」
広「三次元相空間上の成分をそれぞれx, y, zとおいて、次のような非線形常微分方程式を考える。」
dx/dt = 10(y - x)
dy/dt = x(28 - z) - y
dz/dt = xy - 8/3 * z
広「この微分方程式に(x, y, z)の初期条件を与えると、こんな感じのトラジェクトリーが得られる。トラジェクトリーが蝶みたいな領域上で描かれていることが確認できて、この領域がローレンツ・アトラクターだよ。」


🛡元気を半分にして、減少前の🛡元気の130%分パラメーター上昇
レッスン中1回
広「mathematicaが使えるプロデューサーなら、次のコードをコピペして実行すると3Dでトラジェクトリーが確認できるから、色んな初期条件で観察してみて。」
P「大体の輪郭はハート、あるいは蝶みたいな形になっていますが、しっかり見るとトラジェクトリーは全然違いますね。」
tend = 50;
eq = {x'[t] == \[Sigma] (y[t] - x[t]),
y'[t] == x[t] (\[Rho] - z[t]) - y[t],
z'[t] == x[t] y[t] - \[Beta] z[t]};
(*initは初期条件、値を微小変化させて再度実行するとトラジェクトリーが
アトラクター内で大きく変化することが確認できる。*)
init = {x[0] == 10, y[0] == 10, z[0] == 10};
pars = {\[Sigma] -> 10, \[Rho] -> 28, \[Beta] -> 8/3};
{xs, ys, zs} = NDSolveValue[{eq /. pars, init}, {x, y, z}, {t, 0, tend}];
ParametricPlot3D[{xs[t], ys[t], zs[t]}, {t, 0, tend}]エピローグ
広「これでCHAOSの講義はおわり。プロデューサー、どうだった?」
P「話についていくのがやっとでしたが、CHAOSの概要はなんとなく理解できました。篠澤さん、人に教える才能はありそうですね。」
P「最初にCHAOSは聞いたことがある程度と言っていましたが、専門は別の学問領域だったのですか?」
広「そう。専門は素粒子物理学だった。CHAOSについては、ひまなときに論文をちょっと読んでたくらい。」
あまり聞きたくないけど、そろそろはっきりさせないと。
広「……そういえば、今回どうしてCHAOSの講義を受けようって思ったの?」
P「昔、あさり先生からプロデューサーは担当アイドルについて深く理解することが大事ということを学びました。」
広「うん、プロデューサーはわたしのことを一番理解してる。」
P「これまでのレッスンを通して、篠澤さんは簡単なことではなく困難なことに挑戦したい、また純粋に可愛くなりたいということがアイドル活動のモチベーションになっていることは既に把握できています。」
広「……うん。」
改めて面と向かって言われると、恥ずかしい。
P「しかし、これは俺の個人的な考えですが、他人を十分に理解するためにはその人の過去の経験も知る必要もあると思っています。それがたとえ本人にとってつまらないものであっても。」
P「篠澤さんの場合、大学で飽きるほど褒められるという経験がありました。その経験が、今の変態的ともいえる逆境への渇望・レッスンへのモチベーションに繋がっています。」
P「今まではアイドルを目指したい理由について理解しようとしてきました。しかし、篠澤広という人物をさらに理解するためには、アイドルを志すより前の経験についても知る必要があると考えています。」
P「そこで今回篠澤さんには、大学で経験したことについて教えてもらいました。」
広「……プロデューサー、わたしを理解するためにそこまで考えてくれたんだ。」
広「……好き。」
わたしも、プロデューサーになる前の彼のことを知りたい。
広「じゃあ、次はプロデューサーの番。」
P「はい?俺の番とはどういう意味ですか?」
広「DDRのCHAOSについて、おしえて。」
あとがき
こんにちは、KBD合同アドベントカレンダー企画12月21日を担当したなかちん(BBD17th、@nakachin3292)です。今回は学園アイドルマスターに登場する篠澤広の視点から、プロデューサーとCHAOSをテーマにして話すssっぽい怪文書を書いてみました。冬コミで篠澤広が物理について語る同人誌が頒布されるらしいので、それに触発されたのがきっかけです。
……
怪文書を書くにあたって、まずは非線形物理学の本を読みなおす必要がありました。今回話題にした内容については概ね理解できていたつもりでしたが、改めて読み直すと勘違いしている部分があったりして中々大変でした。やっぱり復習は大事。
今回触れたCHAOSの話は弊大学の授業ではまだちょっとしか触れておらず、ほぼ自分の趣味で勉強していました。そのため根本的に勘違いしているところがあるかもしれません。許して
……
物理の復習はまだスムーズに進みましたが、大変だったのがプロデューサーや広の性格・口調をインストールすることでした。
ただでさえ物語文を書いたことがないのに、特定の人物になりきって物語を書くのは本当に難しかったです。でもいざ書いてみると結構楽しかったかも。自分の妄想が言語化されるの癖になるかもしれない。←めっちゃ疲れたので当分は書きません(11/30の自分より)
……
今回の怪文書を執筆するにあたって、RGB/シグさん(@sigu10170921)にはプロデューサーと篠澤広の口調・性格の確認、文章の添削に協力していただきました。この場を借りてお礼申し上げます。
(追記)全部書き終わって今気づいたけど、CHAOSのジャケットの線ってもしかしてトラジェクトリーじゃね?
(追記2)広の新曲のタイトルは【メクルメ】らしいですね、みんな聞きましょう。
参考資料は、
[1]Steven H. Strogatz. 田中久陽 中尾裕也 千葉逸人訳. ストロガッツ 非線形ダイナミクスとカオス. 丸善出版. 2015.
[2]ピエール・ベルジェ イヴェ・ポモウ クリスチャン・ビダル. 相澤洋二訳. カオスの中の秩序 乱流の理解に向けて. 産業図書. 1992.
(グラフとかはwikiから引っ張ってきた)
最後に一言、
広、お誕生日おめでとう!!

しんどいけど楽しそうに走ってるのが広らしくていいよね
