見出し画像

[Python]医療費データを160次元から2次元に圧縮してみた：PCA, MDS, t-SNE, UMAPによる次元削減

あおじる

はじめに

こんにちは、機械学習勉強中のあおじるです。
前回の記事では、医療費データ（160次元）を主成分分析（PCA）してみました。今回は、他の次元削減（次元圧縮）の手法を使って、160次元を2次元に圧縮してみました。

言語はPython、環境はGoogle Colaboratoryを使用しました。

使用するデータ

データは、前回の記事で作成した、全国健康保険協会（協会けんぽ）の加入者基本情報、医療費基本情報から作成した、10年間×47都道府県ごとの医療費の160次元のデータ（性別、年齢階級別の診療種別ごとの「医療費の３要素」）df_yt_C10_sn を使います。
　（10年×47都道府県）×（10指標×性別2区分×年齢階級8区分）
　　＝　470行 × 160次元
の形のデータです。

$$
\def\arraystretch{1.5}
\begin{array}{c:c|c:c:c:c}
\textsf{y} & \textsf{t} & \textsf{KperP\_1\_1\_1} & \textsf{KperP\_1\_1\_2} & \cdots &  \textsf{TperN\_4\_2\_8} \\ \hline
2010 &  1 & {} & {} & {} & {} \\
2010 &  2 & {} & {} & {} & {} \\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\
2010 & 47 & {} & {} & {} & {} \\
2011 &  1 & {} & {} & {} & {} \\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\
2019 & 47 & {} & {} & {} & {}
\end{array}
$$

  • y：年度
    2010～2019 の10年度分

  • t：都道府県
    1：北海道、・・・、47：沖縄 の47都道府県

  • C10_s_n：性別s、年齢階級n別の10指標
    KperP_1_1_1、KperP_1_1_2、・・・、TperN_4_2_8 の160項目

    • C10：診療種別ごとの「医療費の３要素」で、XperY_k（診療種別kのYperX、YperX ＝ Y／X）の形の10指標：

      • KperP_1：１人当たり件数_入院

      • KperP_2：１人当たり件数_外来

      • KperP_3：１人当たり件数_歯科

      • NperK_1：１件当たり日数_入院

      • NperK_2：１件当たり日数_外来

      • NperK_3：１件当たり日数_歯科

      • TperN_1：１日当たり点数_入院

      • TperN_2：１日当たり点数_外来

      • TperN_3：１日当たり点数_歯科

      • TperN_4：１日当たり点数_調剤

    • s：性別
      1：男性、2：女性

    • n：年齢階級
      1：0～9歳、2：10～19歳、・・・、7：60～69歳、8：70歳以上

なお、「医療費の３要素」とは、レセプト統計で、１人当たり医療費（あるいは、１人当たり点数）を次の式で分解したときの３つの要素のことをいいます（前回の記事参照）。

$$
\begin{aligned}
\boxed{\frac{点数}{人数}} &= \boxed{\frac{件数}{人数}} \times \boxed{\frac{日数}{件数}} \times \boxed{\frac{点数}{日数}} \\
\boxed{\begin{matrix} {１人} \\ {当たり} \\ {点数} \end{matrix}}
&= \boxed{\begin{matrix} {１人} \\ {当たり} \\ {件数} \end{matrix}}
\times \boxed{\begin{matrix} {１件} \\ {当たり} \\ {日数} \end{matrix}}
\times \boxed{\begin{matrix} {１日} \\ {当たり} \\ {点数} \end{matrix}}
\end{aligned}
$$

# データ
import pandas as pd
df = pd.read_csv('./df_yt_C10_sn.csv')
print(df.shape)
# (470, 162)
print(df.columns)
# Index(['y', 't', 'KperP_1_1_1', 'KperP_1_1_2', 'KperP_1_1_3', 'KperP_1_1_4',
#        'KperP_1_1_5', 'KperP_1_1_6', 'KperP_1_1_7', 'KperP_1_1_8',
#        ...
#        'TperN_4_1_7', 'TperN_4_1_8', 'TperN_4_2_1', 'TperN_4_2_2',
#        'TperN_4_2_3', 'TperN_4_2_4', 'TperN_4_2_5', 'TperN_4_2_6',
#        'TperN_4_2_7', 'TperN_4_2_8'],
#       dtype='object', length=162)

スケールの異なる３要素のデータですので、前回と同じく、スケーリングして用います。

# 数値部分のみ取り出し
X = df.iloc[:,2:]
print(X.shape)
# (470, 160)

# スケーリング
from sklearn import preprocessing
scaler_ym = preprocessing.MinMaxScaler()
X = scaler_ym.fit_transform(X)
print(X.shape)
# (470, 160)

次元削減（次元圧縮）

この160次元のデータを2次元へ圧縮します。次元削減（次元圧縮）の方法として次の方法をそれぞれ試しました。

結果の表示は、前回と同じで、年度yごと、都道府県tごとに色分けして図示しました。色分けにはseabornのカラーパレットを使いました。

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
# 年度y
label_y = le.fit_transform(df['y'])
cp = sns.color_palette("hls", n_colors=10+1)
color_y = [cp[x] for x in label_y]
# 都道府県t
label_t = le.fit_transform(df['t'])
cp = sns.color_palette("hls", n_colors=47+1)
color_t = [cp[x] for x in label_t]


0．PCA

比較のために、前回の記事のPCA（Principal Component Analysis；主成分分析）の結果を再掲しておきます。

# PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
PC = pca.fit_transform(X)
print(PC.shape) # (470, 160)

n = 2
for i in range(n-1):
  j = i+1
  print('PC{} x PC{}'.format(i+1, j+1))
  plt.figure(figsize=(12,5))
  plt.subplot(1, 2, 1)
  plt.title('PC{} x PC{}, colored by y'.format(i+1, j+1))
  plt.xlabel('PC{}'.format(i+1))
  plt.ylabel('PC{}'.format(j+1))
  plt.scatter(x=PC[:,i], y=PC[:,j], c=color_y)
  plt.subplot(1, 2, 2)
  plt.title('PC{} x PC{}, colored by t'.format(i+1, j+1))
  plt.xlabel('PC{}'.format(i+1))
  plt.ylabel('PC{}'.format(j+1))
  plt.scatter(x=PC[:,i], y=PC[:,j], c=color_t)
  plt.show()

n = 2
for i in range(n):
  for j in range(i+1,n):
    if (i==0 or j==i+1):
      print('PC{} x PC{}'.format(i+1, j+1))
      xmin, xmax = min(PC[:,i]), max(PC[:,i])
      ymin, ymax = min(PC[:,j]), max(PC[:,j])
      plt.figure(figsize=(12,5))
      plt.subplot(1, 2, 1)
      plt.title('PC{} x PC{}, colored by y'.format(i+1, j+1))
      plt.xlabel('PC{}'.format(i+1))
      plt.ylabel('PC{}'.format(j+1))
      plt.xlim(xmin-(xmax-xmin)/20, xmax+(xmax-xmin)/20)
      plt.ylim(ymin-(ymax-ymin)/20, ymax+(ymax-ymin)/20)
      for p in range(10*47):
        plt.text(x=PC[:,i][p], y=PC[:,j][p], s=df.iloc[:,1][p],
                 ha='center', va='center', fontsize=10, color=color_y[p])
      plt.subplot(1, 2, 2)
      plt.title('PC{} x PC{}, colored by t'.format(i+1, j+1))
      plt.xlabel('PC{}'.format(i+1))
      plt.ylabel('PC{}'.format(j+1))
      plt.xlim(xmin-(xmax-xmin)/20, xmax+(xmax-xmin)/20)
      plt.ylim(ymin-(ymax-ymin)/20, ymax+(ymax-ymin)/20)
      for p in range(10*47):
        plt.text(x=PC[:,i][p], y=PC[:,j][p], s=df.iloc[:,1][p],
                 ha='center', va='center', fontsize=10, color=color_t[p])
      plt.show()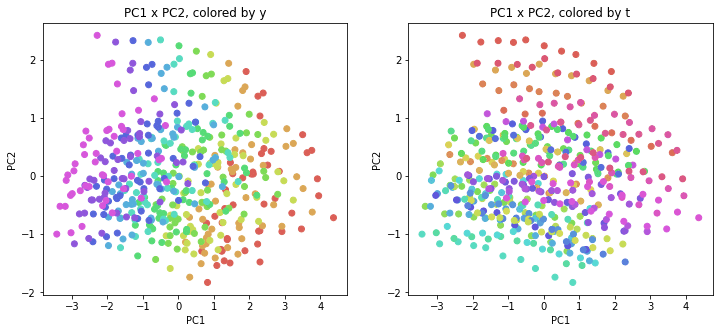
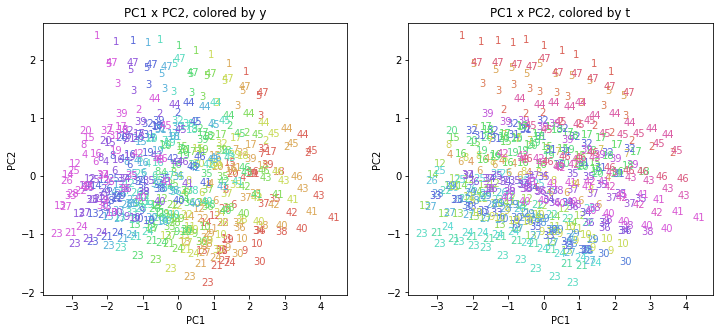
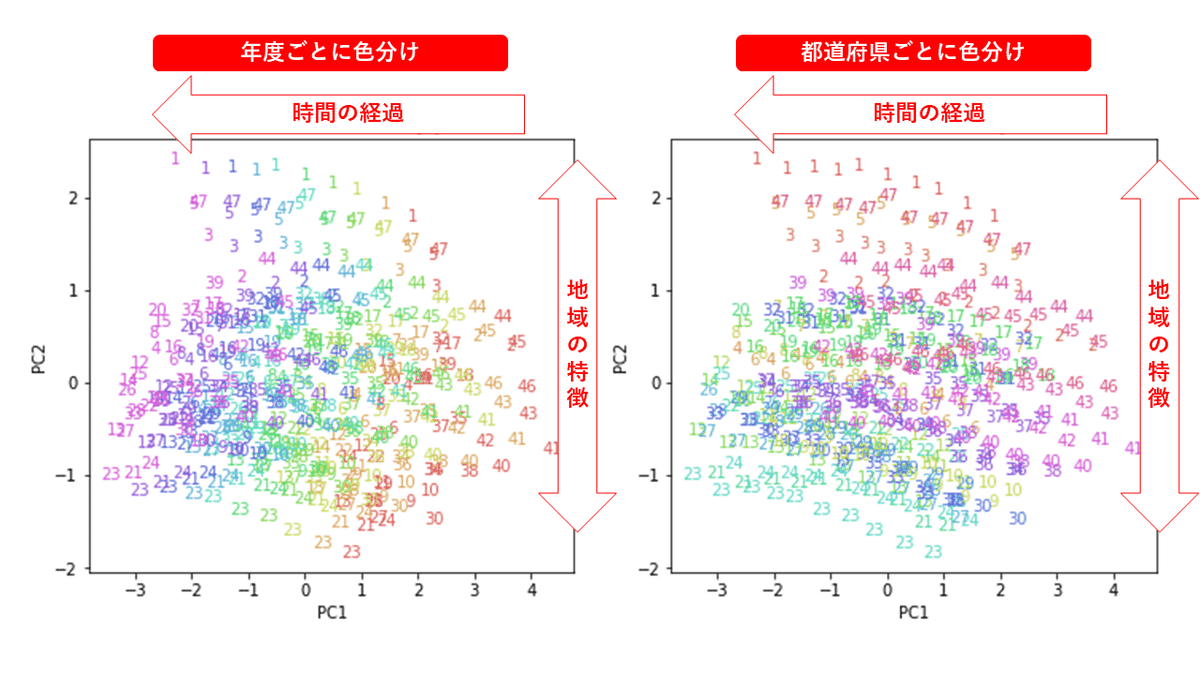
PC1 × PC2
PC1 × PC2
PCAの結果


1．MDS

MDS（Multi-Dimensional Scaling；多次元尺度構成法）を試してみます。

1-1．Metric MDS
使用する距離として、通常のユークリッド距離（euclidean_distances）、マンハッタン距離（manhattan_distances）、コサイン距離（cosine_distances）を試しました。
距離：https://scikit-learn.org/stable/modules/classes.html#pairwise-metrics

ユークリッド距離

# MDS, euclidean_distances
from sklearn.manifold import MDS
embedding = MDS(n_components=2, random_state=0)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape) # (470, 2)

# MDS, euclidean_distances
from sklearn.manifold import MDS
embedding = MDS(n_components=2, dissimilarity='euclidean', random_state=0)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape) # (470, 2)

# MDS, euclidean_distances
from sklearn.manifold import MDS
from sklearn.metrics.pairwise import euclidean_distances
embedding = MDS(n_components=2, dissimilarity='precomputed', random_state=0)
X_transformed = embedding.fit_transform(euclidean_distances(X))
print(X_transformed.shape) # (470, 2)

結果を図示します。前回と同じく、左は年度ごとの色分け、右は都道府県ごとの色分けです。

alg = 'MDS' # algorithm
param = 'euclidean_distances' # parameter
i = 0
j = 1

print('{}, {}'.format(alg,param))
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title('{}, {}, colored by y'.format(alg,param))
plt.xlabel('{}_{}'.format(alg,i+1))
plt.ylabel('{}_{}'.format(alg,j+1))
plt.scatter(x=X_transformed[:,i], y=X_transformed[:,j], c=color_y)
plt.subplot(1, 2, 2)
plt.title('{}, {}, colored by t'.format(alg,param))
plt.xlabel('{}_{}'.format(alg,i+1))
plt.ylabel('{}_{}'.format(alg,j+1))
plt.scatter(x=X_transformed[:,i], y=X_transformed[:,j], c=color_t)  
plt.show()

print('{}, {}'.format(alg,param))
xmin, xmax = min(X_transformed[:,i]), max(X_transformed[:,i])
ymin, ymax = min(X_transformed[:,j]), max(X_transformed[:,j])
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title('{}, {}, colored by y'.format(alg,param))
plt.xlabel('{}_{}'.format(alg,i+1))
plt.ylabel('{}_{}'.format(alg,j+1))
plt.xlim(xmin-(xmax-xmin)/20, xmax+(xmax-xmin)/20)
plt.ylim(ymin-(ymax-ymin)/20, ymax+(ymax-ymin)/20)
for p in range(10*47):
  plt.text(x=X_transformed[:,i][p], y=X_transformed[:,j][p], s=df.iloc[:,1][p],
           ha='center', va='center', fontsize=10, color=color_y[p])
plt.subplot(1, 2, 2)
plt.title('{}, {}, colored by t'.format(alg,param))
plt.xlabel('{}_{}'.format(alg,i+1))
plt.ylabel('{}_{}'.format(alg,j+1))
plt.xlim(xmin-(xmax-xmin)/20, xmax+(xmax-xmin)/20)
plt.ylim(ymin-(ymax-ymin)/20, ymax+(ymax-ymin)/20)
for p in range(10*47):
  plt.text(x=X_transformed[:,i][p], y=X_transformed[:,j][p], s=df.iloc[:,1][p],
           ha='center', va='center', fontsize=10, color=color_t[p])
plt.show()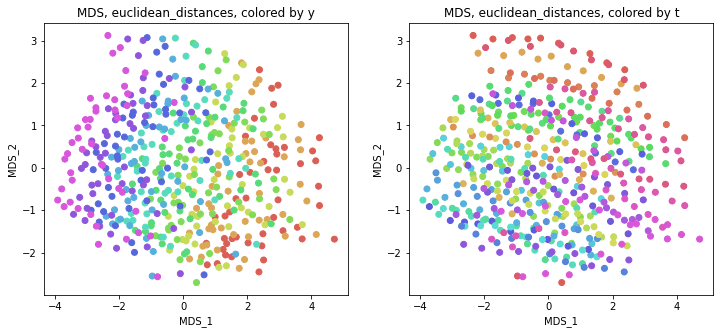
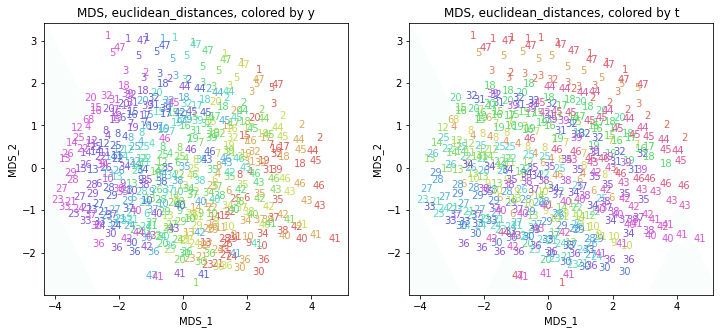
MDS, euclidean_distances
MDS, euclidean_distances

「距離にユークリッド距離を用いた場合は主成分分析と等価」なので、PCAの結果と同じような結果になりました。

マンハッタン距離・コサイン距離

# MDS, manhattan_distances
from sklearn.manifold import MDS
from sklearn.metrics.pairwise import manhattan_distances
embedding = MDS(n_components=2, dissimilarity='precomputed', random_state=0)
X_transformed = embedding.fit_transform(manhattan_distances(X))
print(X_transformed.shape) # (470, 2)

# MDS, cosine_distances
from sklearn.manifold import MDS
from sklearn.metrics.pairwise import cosine_distances
embedding = MDS(n_components=2, dissimilarity='precomputed', random_state=0)
X_transformed = embedding.fit_transform(cosine_distances(X))
print(X_transformed.shape) # (470, 2)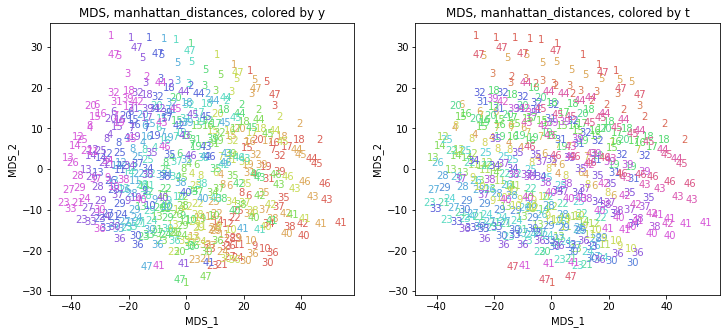
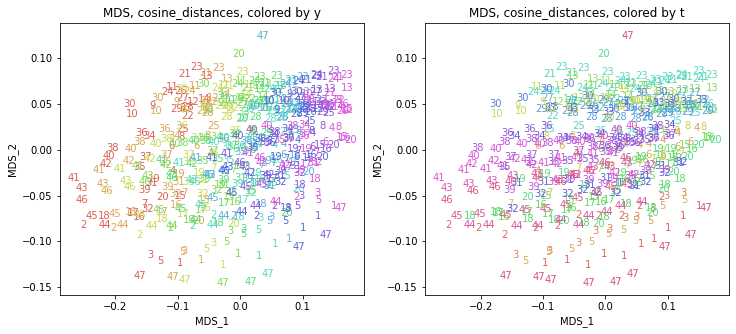
MDS, manhattan_distances
MDS, cosine_distances

他の距離を使ってもだいたい同じような結果になりました。

1-2．Nonmetric MDS

# Nonmetric MDS
from sklearn.manifold import MDS
embedding = MDS(n_components=2, metric=False, random_state=0)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape) # (470, 2)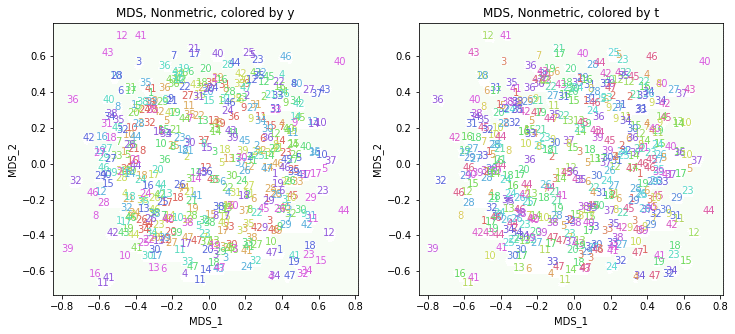
Nonmetric MDS

これはうまくいきませんでした。

2．t-SNE

t-SNE（t -distributed Stochastic Neighborhood Embedding；t分布型確率的近傍埋め込み法）を試してみます。

2-1．perplexity=30.0（デフォルト）
まずはパラメータperplexityをデフォルトの設定で実行してみます。

# t-SNE
from sklearn.manifold import TSNE
embedding = TSNE(n_components=2, random_state=0)
# embedding = TSNE(n_components=2, random_state=0, perplexity=30.0)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape) # (470, 2)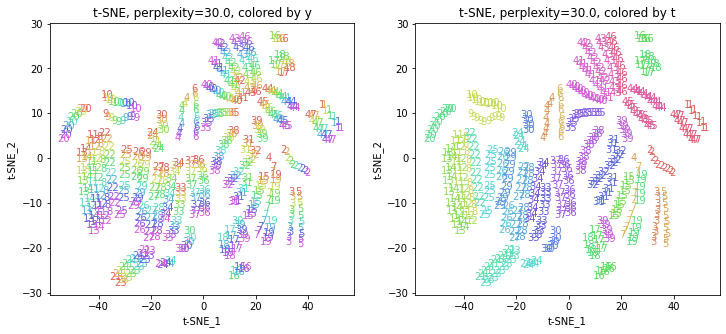
t-SNE, perplexity=30.0（デフォルト）

2-2．パラメータperplexityを動かす
パラメータperplexity（デフォルトでは30.0）を変えて実行してみます（小さい方から大きい方へ）。

# t-SNE
from sklearn.manifold import TSNE
embedding = TSNE(n_components=2, random_state=0, perplexity=2.0)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape) # (470, 2)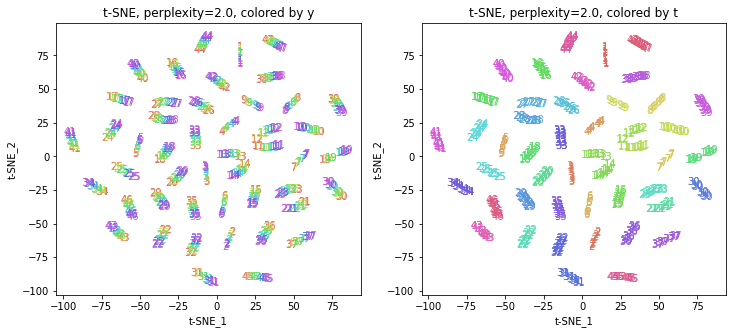
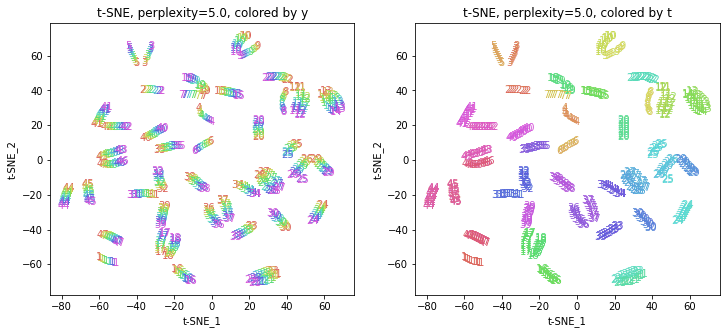
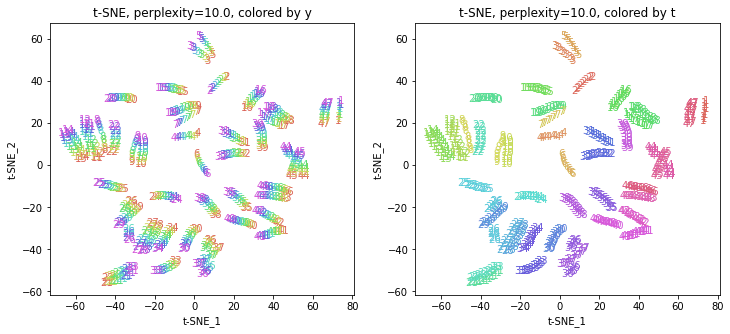
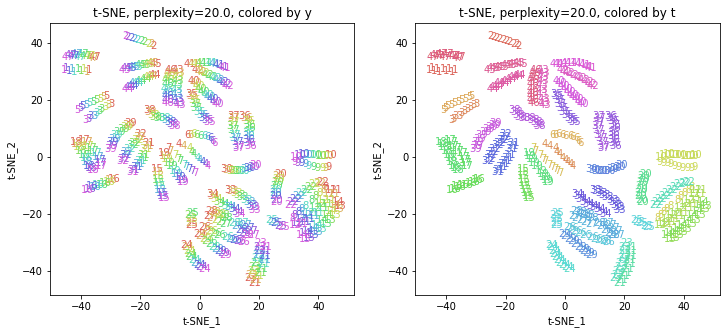
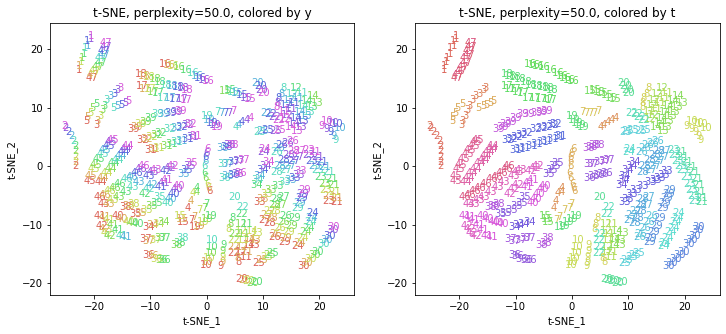
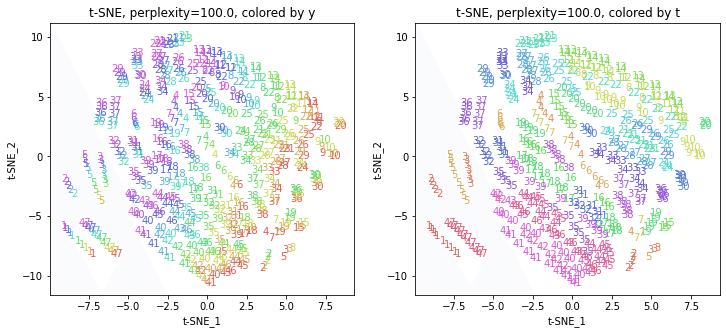
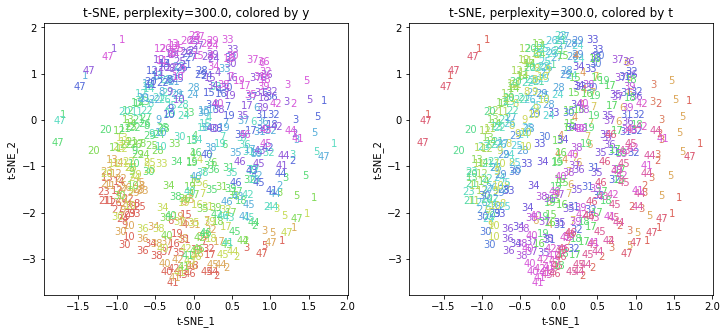
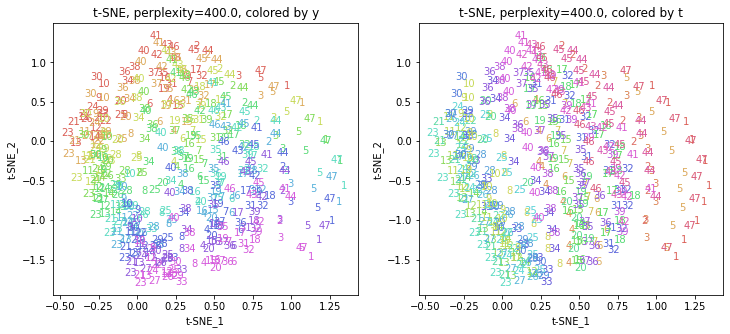
t-SNE, perplexity=2.0
t-SNE, perplexity=5.0
t-SNE, perplexity=10.0
t-SNE, perplexity=20.0
t-SNE, perplexity=30.0（デフォルト）
t-SNE, perplexity=50.0
t-SNE, perplexity=100.0
t-SNE, perplexity=300.0
t-SNE, perplexity=400.0

パラメータperplexityの値が小さいと、都道府県ごとにまとまっていて（都道府県が完全に分離）、年度の向きはばらばらです。パラメータperplexityの値を上げていくと、都道府県同士が近づいていき、年度の向きがそろってきます。さらに上げていくと、年度の向きが完全にそろってきて、PCAやMDSの結果に近い形になっています。
中間のperplexity=20.0～50.0あたりが両方のバランスがとれていてよさそうです。色の近い（地理的にも近い）都道府県が固まって分布しているのがわかります。


3．UMAP

UMAP（Uniform Manifold Approximation and Projection）を試してみます。

UMAPはGoogle Colaboratoryにインストールされていないようなので、インストールしてから用いました。

# UMAP
! pip install umap-learn

3-1．n_neighbors=15（デフォルト）
まずはパラメータn_neighborsをデフォルトの設定で実行してみます。

# UMAP
import umap.umap_ as umap
embedding = umap.UMAP(n_components=2, random_state=0)
# embedding = umap.UMAP(n_components=2, n_neighbors=15, random_state=0)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape) # (470, 2)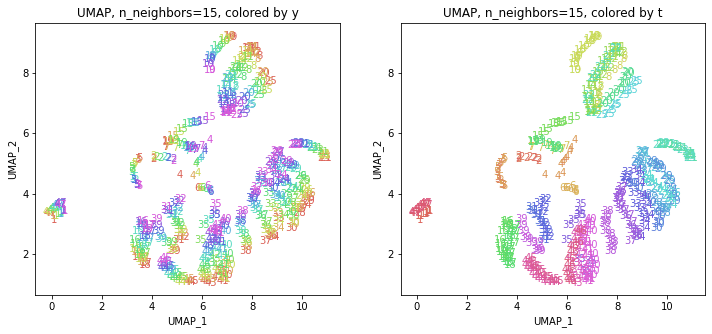
UMAP, n_neighbors=15（デフォルト）

3-2．パラメータn_neighborsを動かす
パラメータn_neighbors（デフォルトでは15）を変えて実行してみます（小さい方から大きい方へ）。

UMAP, n_neighbors=2
UMAP, n_neighbors=5
UMAP, n_neighbors=10
UMAP, n_neighbors=15（デフォルト）
UMAP, n_neighbors=20
UMAP, n_neighbors=25
UMAP, n_neighbors=30
UMAP, n_neighbors=35
UMAP, n_neighbors=50
UMAP, n_neighbors=100
UMAP, n_neighbors=200

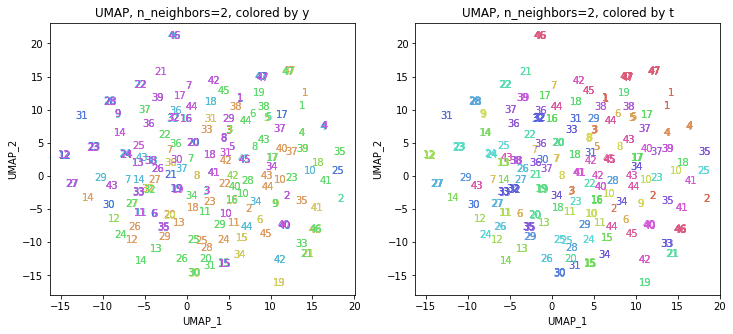
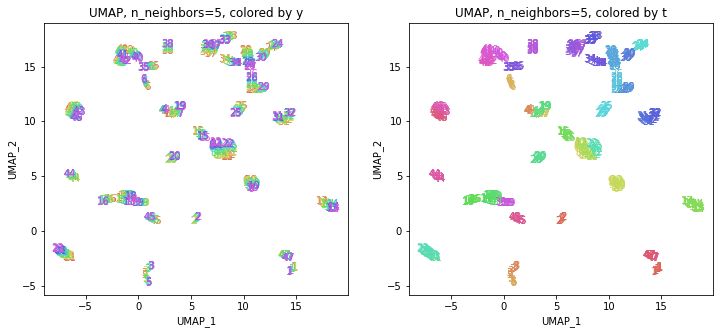
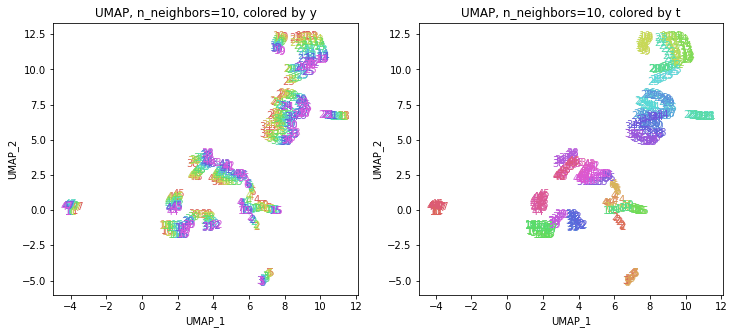
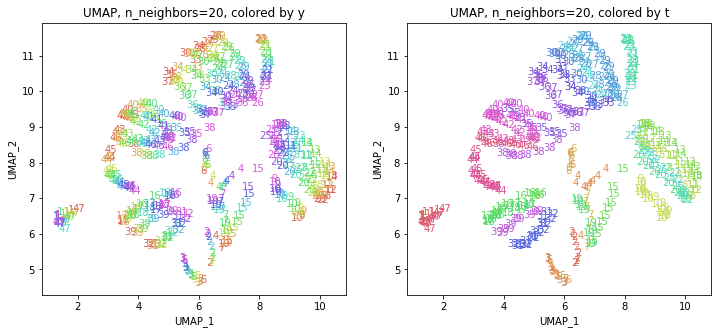
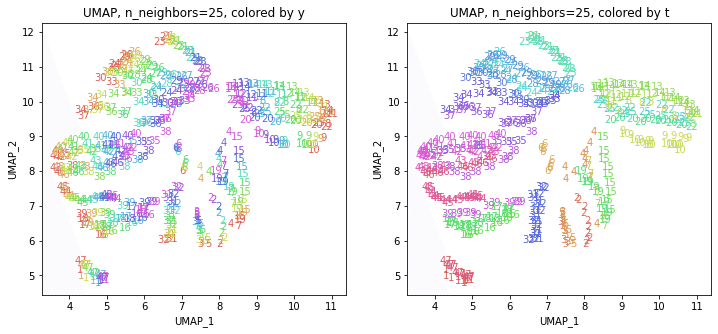
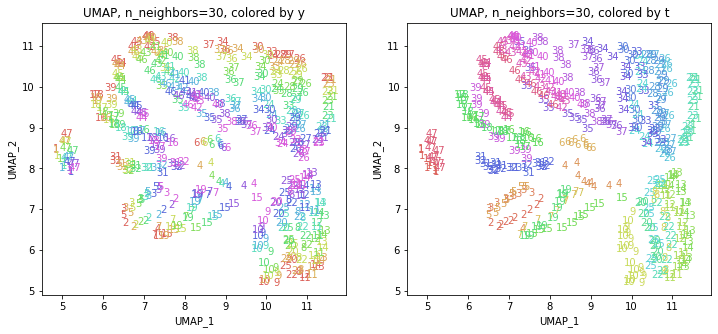
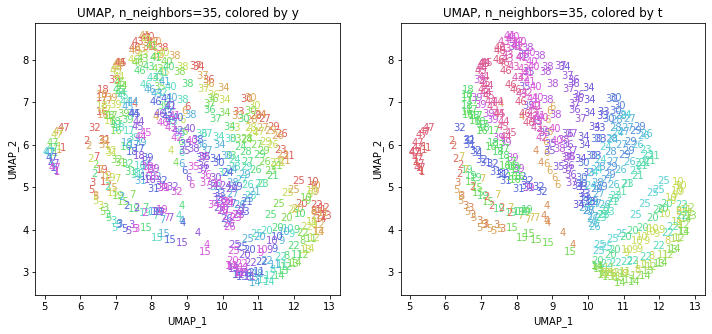
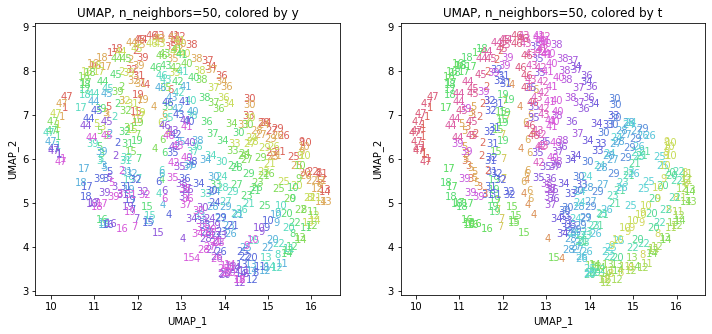
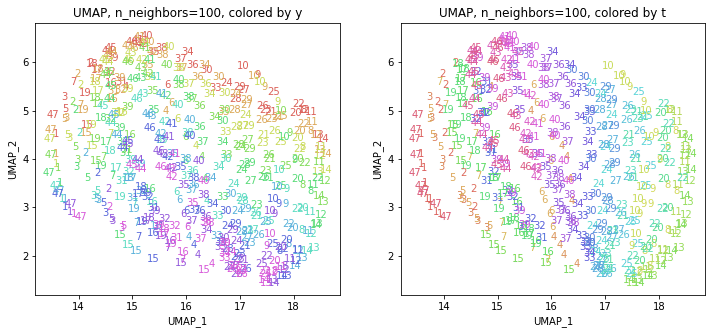
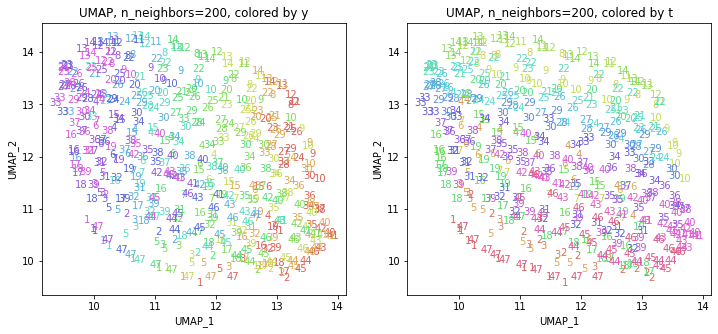
パラメータn_neighborsの値が小さいと、都道府県ごとに分かれていて、パラメータn_neighborsの値を上げていくと、だんだん年度の向きがそろってきます。さらに上げていくと、年度の向きが完全にそろってきて、PCAやMDSの結果に近い形になっています。
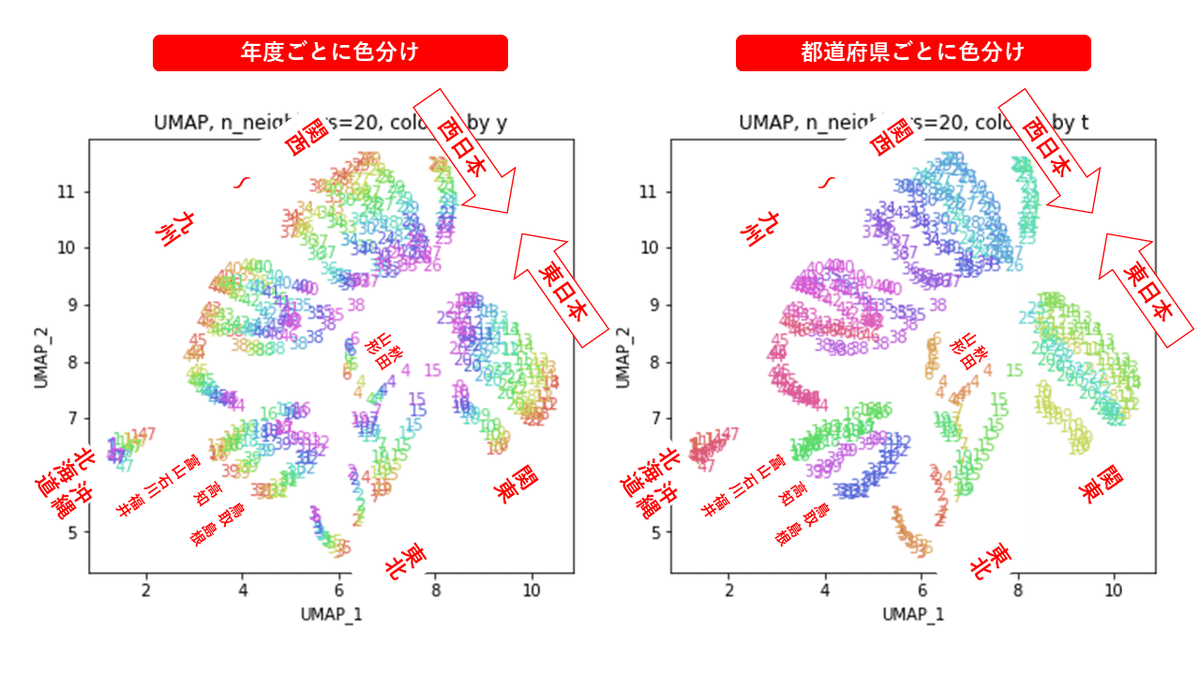
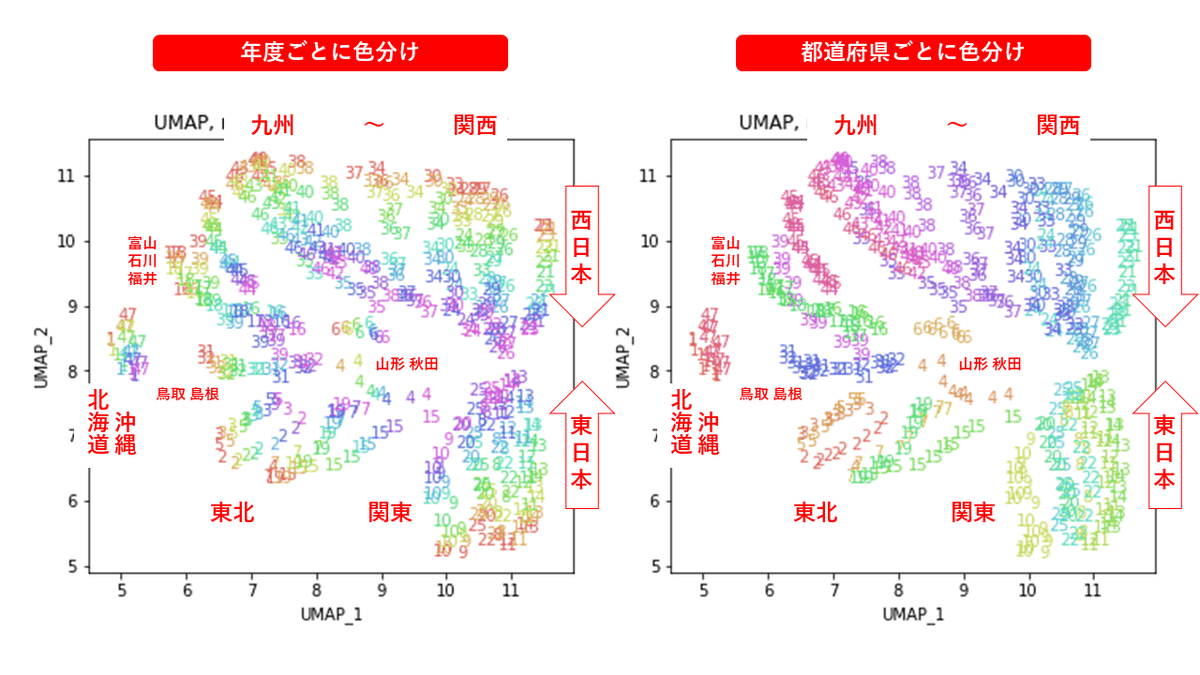
中間のn_neighbors=20～30あたりがバランスが取れていてよさそうです。n_neighbors=20の結果を見ると、左上半分に西日本（関西～九州）、右下半分に東日本（関東・東北）の都道府県が、左下に北海道と沖縄が固まっています。

UMAP, n_neighbors=20 の結果
UMAP, n_neighbors=30 の結果


4．PCA & UMAP

UMAPを単独で実行するのではなく、PCAを実行した結果にUMAPを適用するという方法もあるようです。

参考：
【次元低減】UMAP, PCA, t-SNE, PCA + UMAP の比較｜はやぶさの技術ノート (cpp-learning.com)
UMAP reveals cryptic population structure and phenotype heterogeneity in large genomic cohorts (plos.org)

4.1．PCAの結果をUMAP

# PCA & UMAP

# PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=160)
PC = pca.fit_transform(X)
print(PC.shape) # (470, 160)

# UMAP
import umap.umap_ as umap
embedding = umap.UMAP(n_components=2, n_neighbors=15, random_state=1)
X_transformed = embedding.fit_transform(PC)
print(X_transformed.shape) # (470, 2)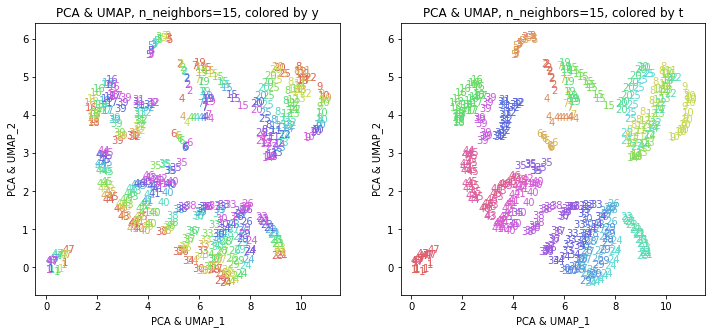
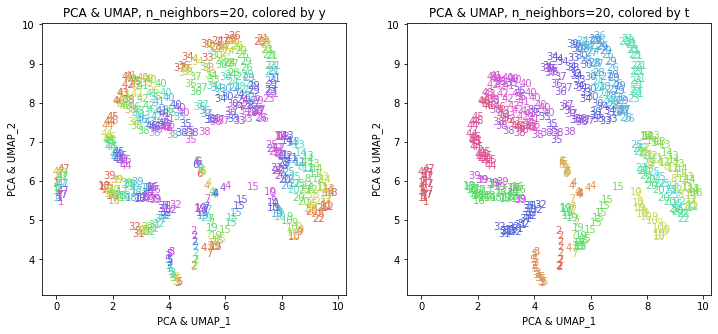
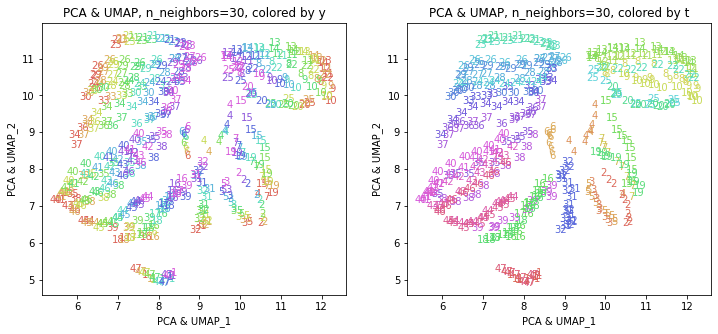
PCA & UMAP, n_neighbors=15
PCA & UMAP, n_neighbors=20
PCA & UMAP, n_neighbors=30

このデータの場合では、UMAP単独の結果とほぼ同じような結果になりました。東日本と西日本に概ね分かれて、地理的に近い都道府県が近くに分布しています。

4.2．PCAの結果の寄与率の高い主成分のみでUMAP

PCAの結果、累積寄与率は第6主成分PC6までで8割、第13主成分PC13までで9割を超えていましたので、PC1～PC6までとPC1～PC13までをそれぞれ使ってUMAPを実行してみます。

import numpy as np
np.set_printoptions(precision=5, suppress=True) # numpyの表示桁数設定
print(pca.explained_variance_ratio_) # 寄与率
print(np.cumsum(pca.explained_variance_ratio_)) # 累積寄与率
# PC6までで8割、PC13までで9割超える

plt.figure()
plt.plot(np.cumsum(pca.explained_variance_ratio_)[:40+1], '-o')
plt.xlabel('principal components')
plt.ylabel('cumulative contribution rate')
plt.grid()
plt.show()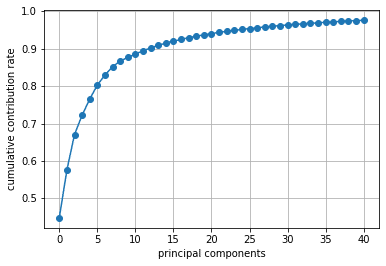
主成分の累積寄与率
# PCA(PC1-PC6) & UMAP
import umap.umap_ as umap
embedding = umap.UMAP(n_components=2, n_neighbors=15, random_state=1)
X_transformed = embedding.fit_transform(PC[:,:6])
print(X_transformed.shape) # (470, 2)

# PCA(PC1-PC13) & UMAP
import umap.umap_ as umap
embedding = umap.UMAP(n_components=2, n_neighbors=15, random_state=1)
X_transformed = embedding.fit_transform(PC[:,:13])
print(X_transformed.shape) # (470, 2)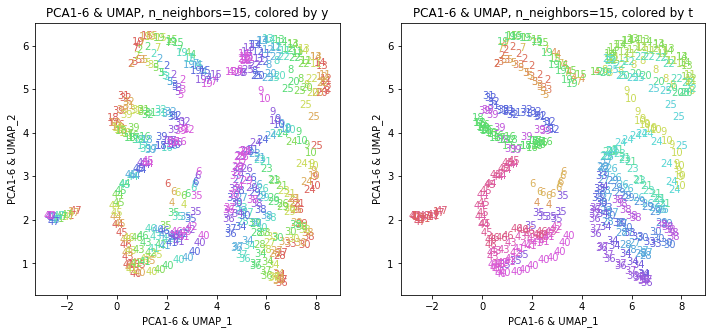
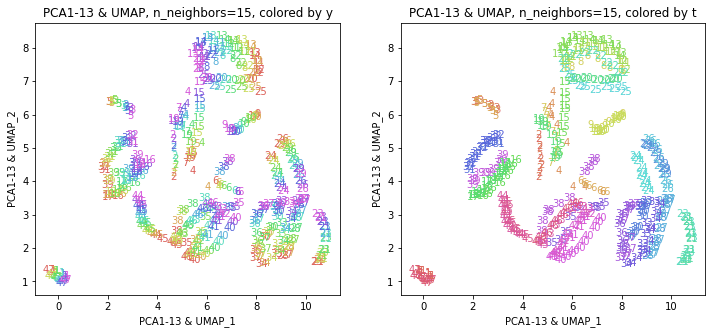
PCA(PC1-PC6) & UMAP
PCA(PC1-PC13) & UMAP

主成分すべてを使った結果と概ね近い結果が得られました。

おわりに

今回は、次元削減のいろいろな手法を使って、160次元の医療費データを2次元に圧縮してみました。2次元まで落としても、年度の推移と地域的な状況をかなりよく表現できていました。また、別の手法を用いても（パラメータによっては）似たような結果になることも確認できました。

最後まで読んでいただき、ありがとうございました。
お気づきの点等ありましたら、コメントいただけますと幸いです。

なお、文中の数式と表は、以下を参考にしました。


#医療費, #医療費の３要素, #医療費分析, #医療費の地域差, #地域差, #地域間格差, #PCA, #MDS, #tSNE, #UMAP, #機械学習, #Python, #協会けんぽ, #noteで数式

この記事が気に入ったらサポートをしてみませんか？