
ボイドモデルで魚群の動きを再現してみた
こんにちは、ANGLERSのエンジニアのリッキーです。みなさんは自然界における集団行動のダイナミックさに魅了されたことはありませんか?
鳥の群れが一斉に方向を変えたり、魚の群れが一糸乱れぬ動きを見せたりする様子は、まさに「生命の神秘」といった感じで、魅力的ですよね。(例えば、下記のNational Geographicの動画)
このような自然界の神秘的で複雑な動きを、コンピュータ上で比較的簡単に再現できる方法があると知ったら、興味が湧きませんか?
それが「ボイドモデル」という理論です。
釣りを通して「魚」を取り扱うANGLERSのエンジニアとして、これは見逃せないと思い検証してみました。その結果を今回のブログでご紹介しようと思います。
ボイドモデルとは?
ボイドモデル(Boid model)とは、群れをなす動物の集団行動を模倣するために1986年にクレイグ・レイノルズ(Craig Reynolds)によって提唱されたシミュレーションモデルです。
▽ボイドモデルの論文はこちら▽
このモデルは、鳥の群れ、魚の群れ、羊の群れなど、自然界に見られる集団行動を模倣することを目的としています。ボイド(Boid)という名称の由来は「bird-oid object(鳥のような物体)」から来ていて、このモデルの中の各個体のことを「ボイド」と言います。
ボイドモデルの3原則
ボイドモデルは、以下の3つの基本原則に基づいています。
Separation(分離)
各ボイド(個体)は、近くにいる他のボイドと衝突しないように動きます。これは、ボイド同士が過度に密集しないようにするためであり、混雑や衝突を避けるために一定の距離を保ちながら移動します。

Alignment(整列)
各ボイドは、近くにいる他のボイドの平均的な移動方向に合わせて、自分の移動方向を調整します。これにより、群れ全体が同じ方向に進むことができ、一体感のある動きが生まれます。

Cohesion(結合)
各ボイドは、近くにいる他のボイドの中心に向かって移動し、群れとしてのまとまりを維持します。これにより、ボイドは散らばりすぎることなく、一定の集団を形成します。
(この「結合」は「分離」と一見相反するように見えますが、実際にはボイドの相互作用において異なる範囲で作用するため、棲み分けがされています。それぞれ異なる役割を果たすことで、ボイド群が複雑でリアルな動きを再現できます。)

これらの原則は非常にシンプルですが、相互に作用することで、ボイド群の自然な移動パターンを複雑かつリアルに再現します。分離が過度であれば群れがばらけてしまう一方、結合が強すぎると密集しすぎて動きが阻害されるため、これらのバランスが重要です。
このように、3つの比較的シンプルな原則を組み合わせることで、群れの複雑な動きを模倣できるのがボイドモデルの優れたポイントです。
ボイドモデルは、まずアニメーションの世界で使われ始めました。群れのリアルな動きを再現するための技術として採用され、多くのアニメーションや映画で利用されています。
その後、このモデルはさらに応用範囲を広げ、ロボット工学や人工生命研究などにも利用されるようになりました。現在では、自然界の生命現象を解明するための研究にも使われており、群れ行動の理解や、さまざまなシステムの設計・シミュレーションに役立てられています。
ボイドモデルの数式
さて、次にボイドモデルにおいて、群れの動きを決定する数式を見ていきます。
なお、ここで記載する数式はあくまで一例であり、実際には上記のボイドモデルの概念に基づいて、利用シーンに基づいた最適な数式を用いればよいです。
Separation(分離)の数式
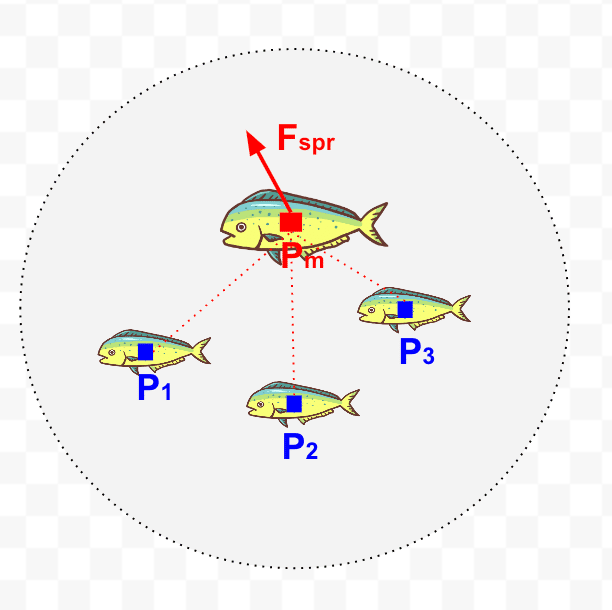
自分の近くにいる別の魚と離れようとする作用のSeparation(分離)によって、各ボイドにかかる力$${F_{spr}}$$は次のようになります。
$$
\mathbf{F_{spr}} = \sum_{i=1}^N\frac{\mathbf{P_m}-\mathbf{P_i}}{|\mathbf{P_m}-\mathbf{P_i}|^2}
$$
ここで、
$${P_{m}}$$は作用対象のボイド$${m}$$の位置ベクトル
$${P_{i}}$$はボイド$${m}$$の近くにいるボイド$${i}$$の位置ベクトル
$${N}$$は、ボイド$${m}$$の近くにいるボイドの個数
です。
また、分母に$${m}$$と$${i}$$の距離の二乗を置いているのは、近くにいるボイドの影響を大きくし、遠くにいるボイドの影響を小さくするためです。
Alignment(整列)の数式

自分の近くにいる群れと同じ方向に進もうとする作用のAlignment(整列)によって、各ボイドにかかる力$${F_{alg}}$$は次のようになります。
$$
\mathbf{F_{alg}} = \mathbf{v_{avg}} - \mathbf{v_{m}}
$$
但し、ここで$${\mathbf{v_{avg}}}$$はボイド$${m}$$の近くにいる群れの速度ベクトルの平均であり、以下のように計算できます。
$$
\mathbf{v_{avg}} = \frac{\sum_{i=1}^N \mathbf{v_{i}}}{N}
$$
Cohesion(結合)の数式

自分の近くにいる群れの中心に集まろうとする作用のCohesion(結合)によって、各ボイドにかかる力$${F_{chs}}$$は次のようになります。
$$
\mathbf{F_{chs}} = \mathbf{P_{center}} - \mathbf{P_m}
$$
但し、ここで$${\mathbf{P_{center}}}$$は近くの群れの各ボイドの中心点であり、以下のように計算できます。
$$
\mathbf{P_{center}} = \frac{\sum_{i=1}^{N} \mathbf{P_i}}{N}
$$
3つの力の相互作用(合計)
ここまで、ボイドモデルの3原則について、それぞれボイドに加わる力を見てきましたが、ボイドモデルはこれら3つの力の相互作用(合計)によって成り立ちます。
つまり各ボイドに加わるのは、各作用(Separation / Alignment / Cohesion)を足し合わせた力になり、下記のように表現できます。
$$
\mathbf{F_{m}} = w_{spr}\mathbf{F_{spr}} + w_{alg}\mathbf{F_{alg}} + w_{chs}\mathbf{F_{chs}}
$$
ここで、$${w_{*}}$$は各作用に対する重み係数であり、これらを自由に調整することで様々な群れの動きを作りだすことができます。
位置情報の更新
さて、ここまでで、各ボイドに加わる力を出すことができました。
ボイドモデルは群れの「動き」をシミュレーションするためのものであり、動きを計算するためには、各ボイドが持つ位置をタイムステップごとに更新していく必要があります。
いま、各ボイドはそれぞれ現時点(現ステップ)での位置$${P^t}$$と速度$${v^t}$$を持っており、次ステップの位置$${P^{t+1}}$$を求めるためには、まず、次ステップの速度$${v^{t+1}}$$を計算します。

次ステップの速度$${v^{t+1}}$$は、現ステップの速度$${v^{t}}$$に、ボイドモデルの相互作用力である$${F_m}$$を加えたものであり、下記のようになります。
$$
\mathbf{v_{m}^{t+1}} = \mathbf{v_{m}^{t}} + \mathbf{F_{m}}
$$
次ステップの速度$${v_{m}^{t+1}}$$が求まったので、次ステップの位置$${P_m^{t+1}}$$は、単純に以下のように求めることができます。
$$
\mathbf{P_m^{t+1}} = \mathbf{P_m^t} + \mathbf{v_m^{t+1}}
$$
以上がボイドモデルの数式になります。
このような一連の計算を、各ボイドに対して、各ステップごとに繰り返し計算することによって、群れの動きをシミュレーションすることになります。
シミュレーション実装
ここまで理論をまとめてきましたが、ここからは実際にシミュレーションを実装していきます。
Blenderを利用
今回は3D統合ツールのBlenderを利用して、3次元空間上で魚群の動きをシミュレーションしました。
Blender上の実装をブログ形式でまとめるのは難しいため、実装の詳細公開は別の機会にしたいと思いますが、イメージとしては以下のように、BlenderのGeometry Nodes内のSimulation Nodes機能を利用することで、タイムステップごとの各ボイドの位置をボイドモデルの3原則に基づいて更新していきます。
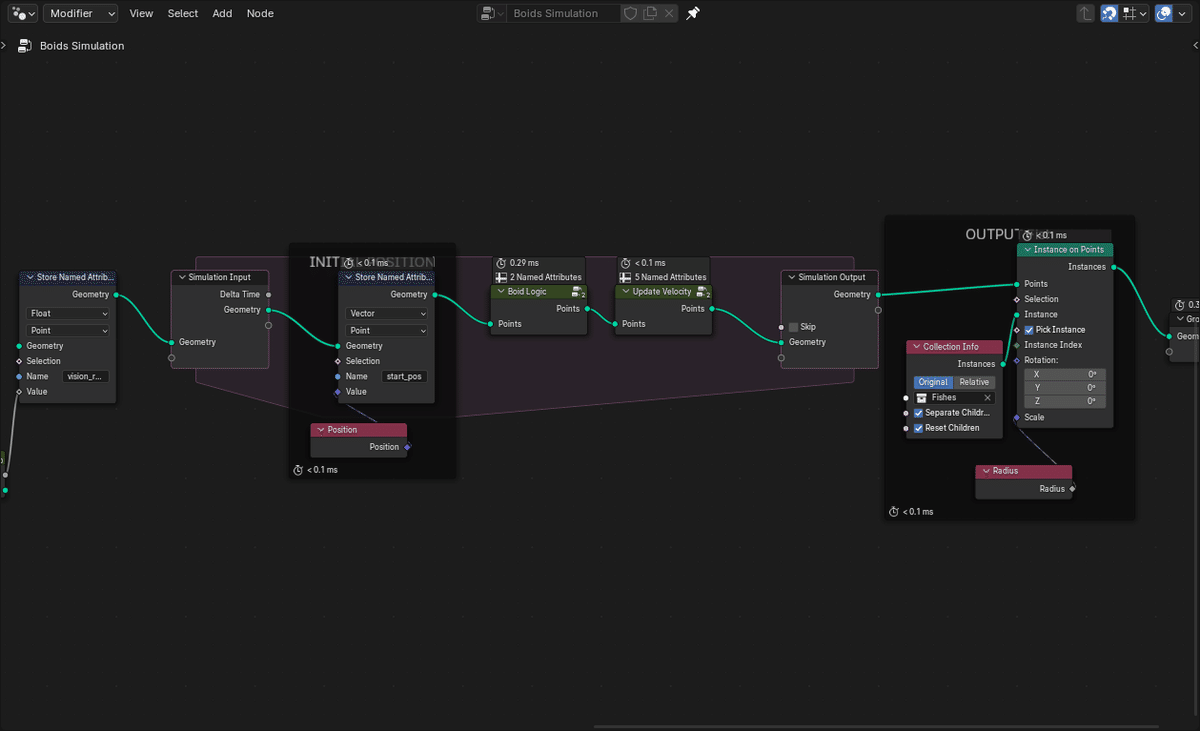


シミュレーション条件
次はいよいよ、実際のシミュレーション結果を見ていきます。
なお今回のシミュレーションは下記のような条件になっています。
ボイドとして200匹の魚を利用
初期状態では立方体の範囲内で各ボイドをランダムに配置
初期状態のボイドの向きや初速もランダムに決定
その後、ボイドモデルのロジックにしたがって各ボイドの速度、位置を更新
移動可能な範囲として球体を設定し、その境界からは出ないように速度、位置を更新
ボイドモデルの3原則のそれぞれについて挙動を把握するためにも、まずは、それぞれ1つの作用のみに絞った場合の結果を見ていきます。
Separation(分離)のみ
まず最初は、Separation(分離)のみに力の作用を限定した場合、魚群は以下の動画のような動きとなりました。
動画からも分かるように、各ボイドは他のボイドから距離を取るように散らばっていき、最終的には球体の境界内で均等に位置することになります。
Alignment(整列)のみ
次に、Alignment(整列)のみに力の作用を限定した場合、魚群は以下の動画のような動きとなりました。
動画からも分かるように、各ボイドは周辺の魚群と向きを合わせるように位置を更新していき、最終的には境界に沿ってすべてのボイドが同じ向きに整列して位置を更新していきます。
Cohesion(結合)のみ
次に、Cohesion(結合)のみに力の作用を限定した場合、魚群は以下の動画のような動きとなりました。
動画からも分かるように、各ボイドは周辺のボイドと結合するように位置を更新し、最終的にはいくつかの魚群に分かれて、複数のボイドが1つの塊を形成していきます。
ボイドモデル:3つの相互作用
最後に、3つの作用をすべて組み合わせたボイドモデルの場合、魚群は以下の動画のような動きとなりました。
動画からも分かるように、各ボイドが、これまで見てきた3つの力(Separation / Alignment / Cohesion)の相互作用を受けることにより、魚群として自然な動きを再現できていることがわかります。
まとめ
今回は、鳥や魚などの集団行動をシミュレーションするための理論であるボイドモデルについてまとめました。
ボイドモデルの素晴らしい点は、シンプルなルールを組み合わせることで、複雑な群れの動きを再現できることです。今回紹介した基本的なボイドモデルのロジックに加えて、
外敵(捕食者など)をモデルに加え、外敵から逃げる動き
誘致物(餌など)をモデルに加え、誘致物に向かう動き
などもシミュレーションに取り入れることが可能です。
これにより、最初に紹介したNational Geographicの動画のような、より精密な自然界の群れの動きを再現できます(これらについては機会があれば続編として書きたいと思います)。
一方で、ボイドモデルは群れの動きを「模倣」しているに過ぎず、実際の群れの動きのロジックはまだ解明されていない部分も多いです。
しかし、このような模倣を起点に、生命の真のロジックを解明しようとする「人工生命(ALIFE)」という研究分野も存在します。この分野は、人工知能(AI)とも理論や技術的に隣接する領域であるため、これからも注目していきたいです。
最後までお読みいただき、ありがとうございました。
参考文献:
https://www.red3d.com/cwr/papers/1987/boids.html
https://www.amazon.co.jp/dp/4873118476
https://cattech-lab.com/science-tools/lecture-8-2-boid-equation/
一緒にはたらく仲間を積極採用中!!
アングラーズでは、様々なポジションで積極採用を行っています。
少しでも気になった方は、以下よりエントリーをお待ちしております!

この記事が気に入ったらサポートをしてみませんか?
