
第11章 「吸引力の正体」
「学問こそが最高の娯楽である」シリーズの第11章。このシリーズは毎週土曜日18時前後にアップします。
さて、気合を入れて書いた前回の記事は話が抽象的すぎたのか反応がイマイチだったようなので、今回はちょっと趣向を変えてみます。
「吸引力」の話をしましょう。
1. 吸引力とは
吸引力と聞いて、どういうイメージを持ちますか?
字面を見れば、シンプルに「吸い込む力」ということになるでしょう。
「吸い込む」で思い浮かべることと言えば、ヘッダーのイラストに上げた掃除機がありますね。
まさに埃を吸引するのが仕事です。
他には例えばこれ。
飲み物を吸い込むストローがあります。
ストローはジュースなどの飲み物を吸い込むための道具ですね。
人がストローを使って飲み物を吸い込むとき、どうやるかというと、肺の吸引力を使って吸い込みますね。
つまり、肺に空気を吸い込む行為も吸引です。
他にも、人それぞれ色々な吸引のパターンを思い浮かべられると思います。
さて、「吸引力なんて、本当は実在しない」と言われたら、どう思います?
「は?」
ってなりますよね。
今回はそのカラクリの話です。
2. 体積と圧力
おそらく皆さんが小学校のころに、理科の授業で次のような実験をやったと思います。
注射器(シリンダー)をつかった圧力の実験。
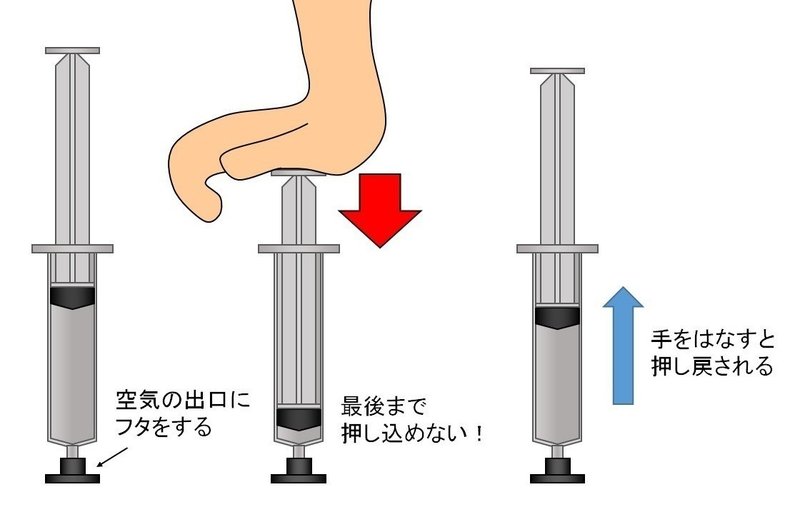
中に空気を閉じ込めた状態で、シリンダーを押すとある程度まで圧縮できるけど、押し込むほどに押し返す力が強くなってある所以上は押し込めなくなります。
そして押し込んでいた手をはなすと、シリンダーはほぼ元の位置まで押し戻されます。
これは高校生で習う「ボイルの法則」という現象の実験です。
密閉された空気の体積と圧力は反比例の関係になります。
例えば、空気の体積が半分になると、圧力がほぼ2倍まで増えるし、体積が2倍になれば圧力は半分まで減るという関係が成り立っています。
シリンダーで空気を10分の1まで圧縮すれば、中の圧力はほぼ10倍です。
ピストンの直径が1 cmだとすると、10分の1まで圧縮したときに押し返される力は約7.2 kg重に達します。
これは大人の砲丸投げの選手が投げている砲丸の重さに近い数字ですね。
さて、一方で引っ張る実験というのもやったと思います。
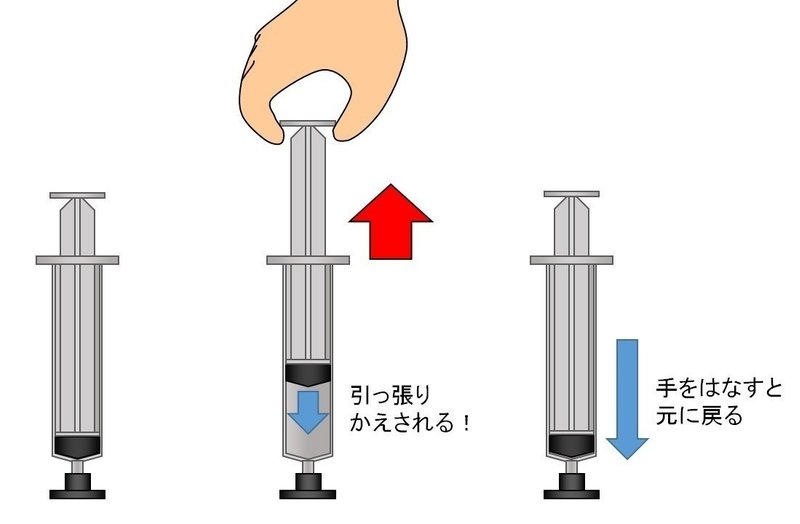
シリンダーの中に空気がない状態からピストンを引っ張ると、内側に引っ張り返されて、手をはなすと元の位置に戻ってしまいます。
内側に引き込まれるわけですから、吸引力ですね。
実際、シリンダーの先端を水面に浸けた状態でピストンを引っ張ると、シリンダーの中に水が吸い込まれます。
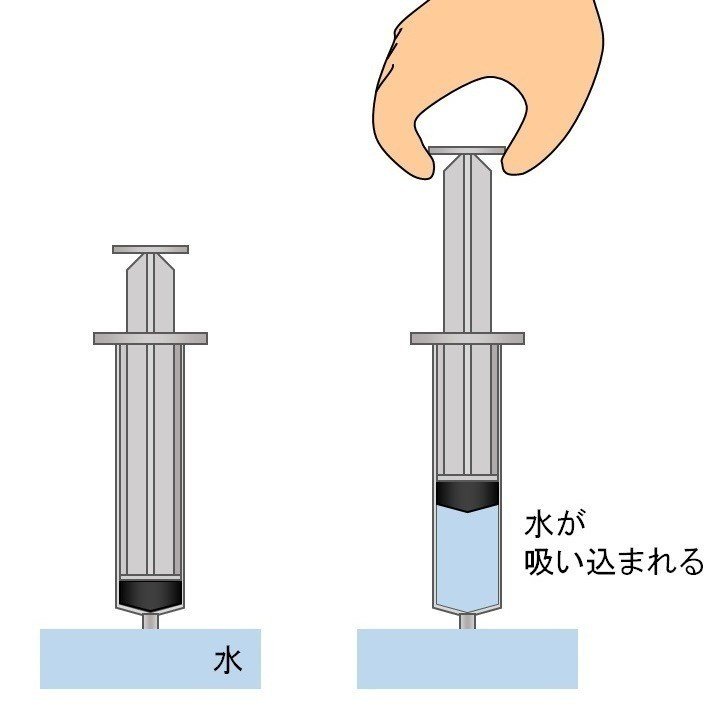
なんやねん。
やっぱり吸引力は存在するやん!
・・・そう見えるんですけどね。
実は、違うんです。
3. 壁の押し引き
ここで、少し簡単な物理の話をしましょう。
水平な地面の上に置かれた、地面との摩擦がない壁をイメージしてください。
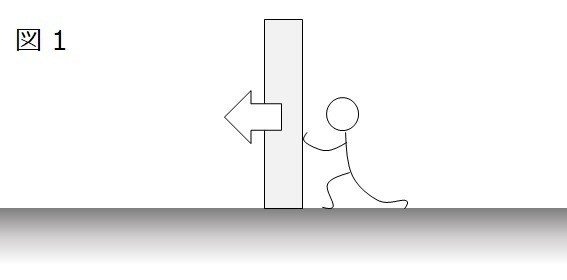
図1のように、誰かが右側からこの壁を押したとすれば、壁は左側に動きます。(壁が倒れるだろうというツッコミはなしね。)
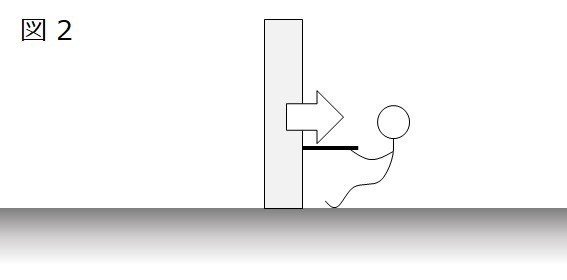
次に、図2のように、壁に取っ手をつけて右側から引っ張ったらどうでしょう?
当然、壁は右側に動きます。
では3つ目。
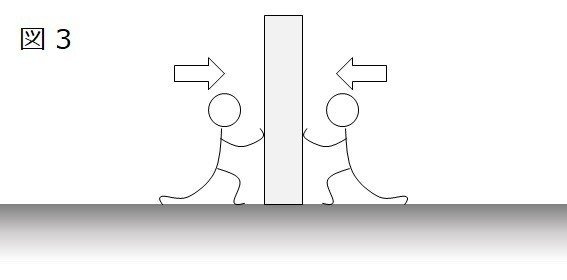
右と左、両方から壁を押したらどうなるでしょう?
左右から押す人の力が全く同じなら壁は動きません。
しかし、どちらかの人の押す力の方が強ければ、壁は押す力が弱い人の側に動きます。
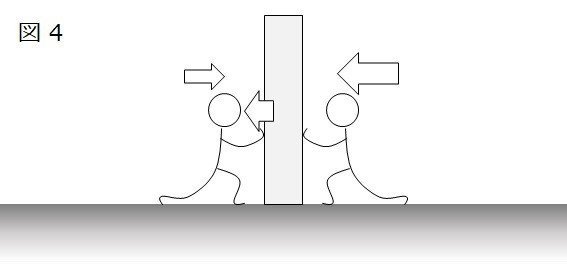
図4のように、右側の人が強ければ、壁は左側に動きます。
物凄く当たり前の話ですね。
急になんの話やねんと。
3. 吸引力の正体
それでは、シリンダーの話に戻りましょう。
ピストンを押し込んで空気を圧縮する場合、下の図のようなイメージになります。
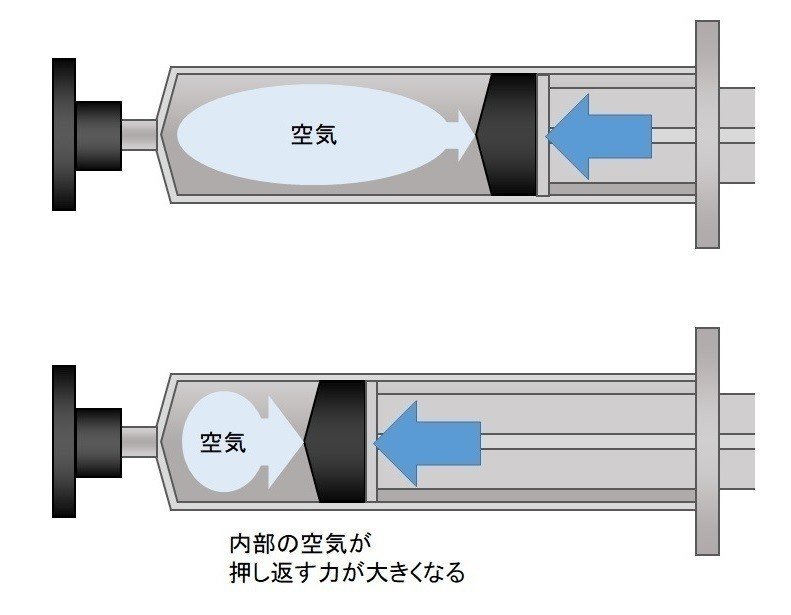
中の空気が圧縮されると圧力がどんどん上昇して、内側から押し返す力が大きくなります。
ちょうど前節の図3と図4に近いですね。
そして、あるところで外から押し込む力と内側から押し返す力がつり合って、それ以上は押し込めない状態になります。
では引くときはどうでしょう?

内部にはほぼ空気がない真空に近い状態ですので、内側から押されることはないのですが、逆に誰かが内側に引っ張ることもありません。
それなのに、ピストンは内側に引き込まれるような抵抗を示します。
真空がひっぱっているじゃないの?
違います。
正解は、「外から大気圧が押している」です。
図で書くとこうなります。
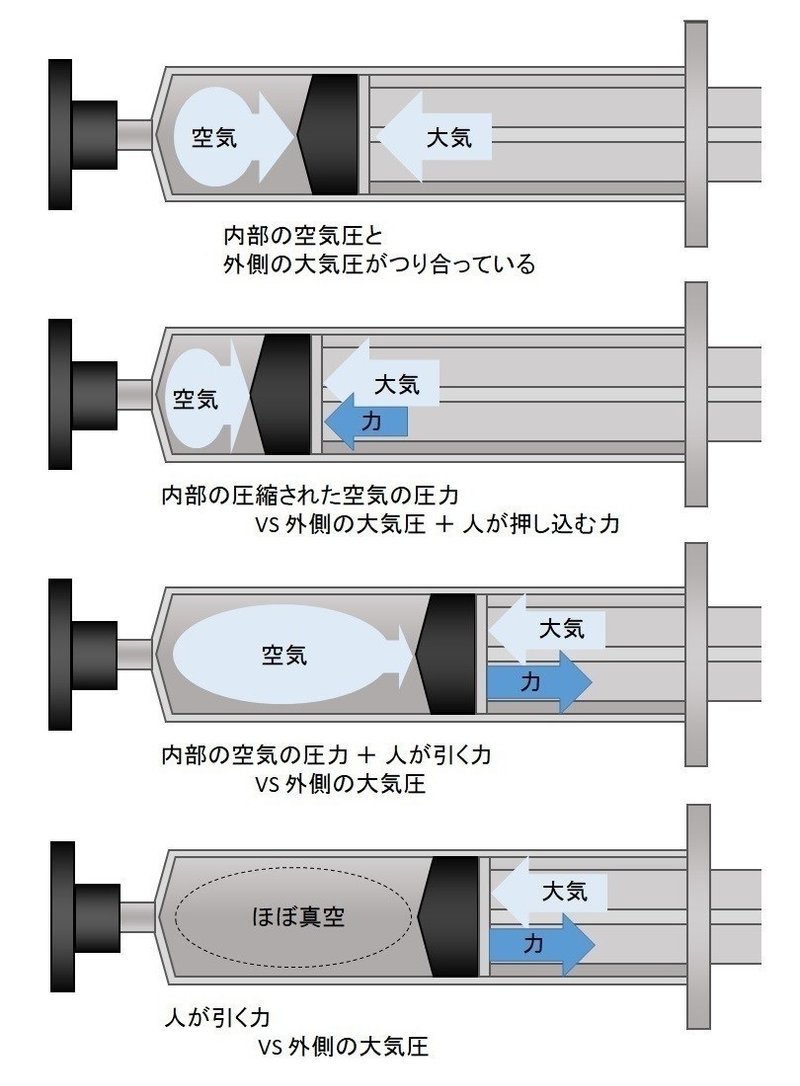
中に空気がある場合でも、膨張すれば内側から押す力が弱まるので、その分だけ大気圧の抵抗を感じることになります。
「吸引力」というのは、実際には「吸引されるような感覚」というだけで、逆に大気が押しているわけです。
吸引力の正体は大気圧なのです!
4. ストローの話
さて、次はストローで液体を吸い上げる場合について解説します。
前節で、吸引力の正体は大気圧だといいましたが、だとするとストローで液体を吸い上げることができるのはなぜか?
やはり、これも大気圧が押しています。
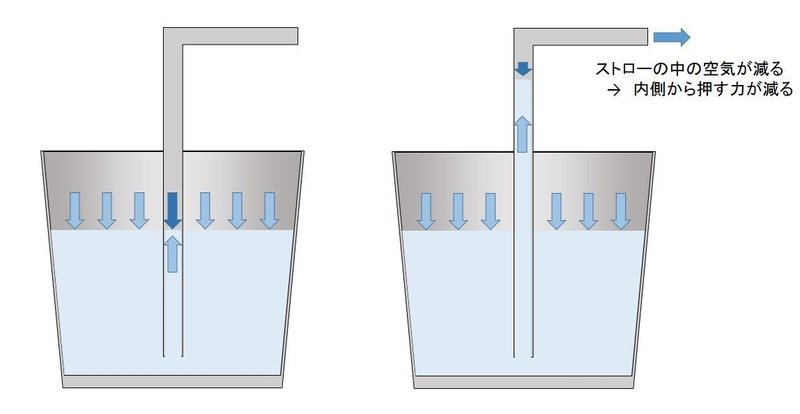
図の左側の様に、普段はストローの内側の空気の圧力は大気圧と同じなので、コップの液面を大気が押す力とつり合って、ストローの内側の液体は動きません。
しかし、図の右側の様に、ストローの中の空気が減ると、ストローの内側から液面を押す力は弱くなり、大気圧がコップの水面を押す力に負けて、ストローの液面が上がってくるのです。
「吸引力」が引っ張っているのではなく、「大気圧」が押している。
これを証明する現象があります。
実は、どんなに高性能なバキュームポンプを使っても、およそ10 m下に水面がある井戸からパイプを使って水を吸い上げることはできません。

これは、10 mの高さの水の水圧がちょうど1気圧に相当するからです。
パイプの中が真空になると、ストローの場合と同じく大気圧が井戸の水面を押す力でパイプの中の水が押し上げられていきます。
しかし、水が井戸の水面から約10 mの高さまで上がってくると、パイプの中の水にかかる重力が、下から押し上げる大気圧とちょうどつり合ってしまうため、それ以上水面を上げることができないのです。
この原理は、発見したイタリア人物理学者の名前をとって「トリチェリの真空」と呼ばれています。
トリチェリは真空のガラス管の中に水の代わりに比重の重い水銀を閉じ込めたものを使えば、同じ原理で大気の圧力を測れることを発見しました。
これが世界ではじめて気圧の測定を可能にした「水銀気圧計」です。
水銀気圧計自体は現在ではほとんど見ることはありませんが、名残りとして、血圧測定などに使われる圧力の単位に「mmHg(ミリメートルエイチジー)」が使われていますね。
「Hg」は水銀の元素記号なのです。
また、「mmHg」はトリチェリの名前からとった「Torr(トル)」という単位を使う場合もあります。
5. 掃除機のパワー
さて、なんでこんな話を長々と説明したのかというと、一時期流行った掃除機の吸引力で重りを持ち上げるコマーシャルのカラクリを知ってもらいたかったからです。
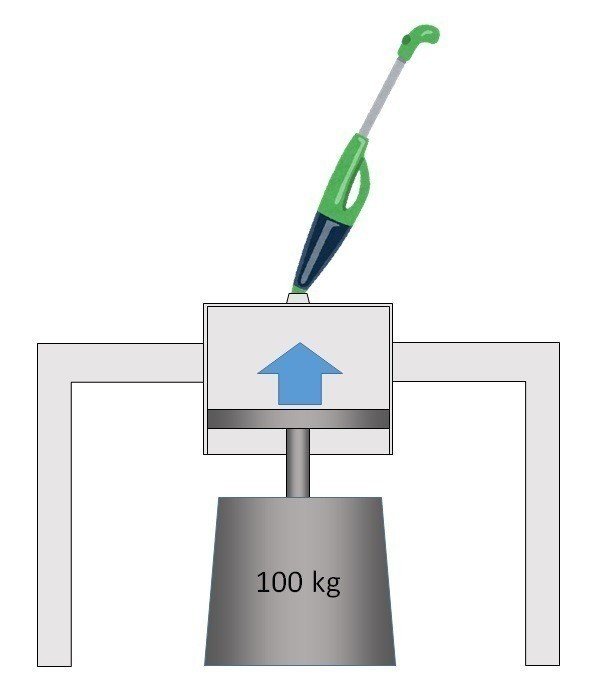
うちの掃除機の吸引力なら100 kgの重りを持ち上げられます!
みたいなパフォーマンスを見せられると、「おお!すげえ!」ってなりますよね。
でもこれ、原理的にはそんなに凄くないんですよね。
だって、実際に重りを持ち上げているのは大気圧なんです。
掃除機の性能を表す数値の中に、真空度というのがありまして、数kPaから20~30 kPaなど、ピンキリです。
これはどれぐらい減圧できるかを示した数値です。
大気圧がおよそ100 kPaですので、真空度20 kPaと書かれた掃除機は約0.2気圧分の減圧が可能だということを意味します。
なので、上の図の装置で真空度20 kPaの掃除機をセットした場合、差し引きで0.2気圧分の力がピストンを押し上げてくれます。
これがどれぐらいの重さを持ち上げる力になるのかわかりますか?
答えは「ピストンの面積による」なんです。
圧力というのは「単位面積当たりの力」なので、ピストンの面積が大きければ大きいほど、同じ圧力でも押す力は大きくなります。
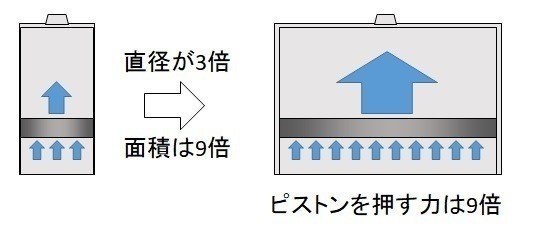
例えば直径10 cmのピストンなら、0.2気圧は約16 kg重の力になりますので、100 kgの重りはびくともしません。
しかし、直径30 cmのピストンなら、0.2気圧は約146 kg重の力になります。
100 kgの重りも軽々と持ち上がります。
仮に世界一高性能な真空ポンプでシリンダ内部を完全に真空にしたとしても、ピストンの直径が5cmしかなかったとしたら、持ち上げられる重量は20 kgが限度です。
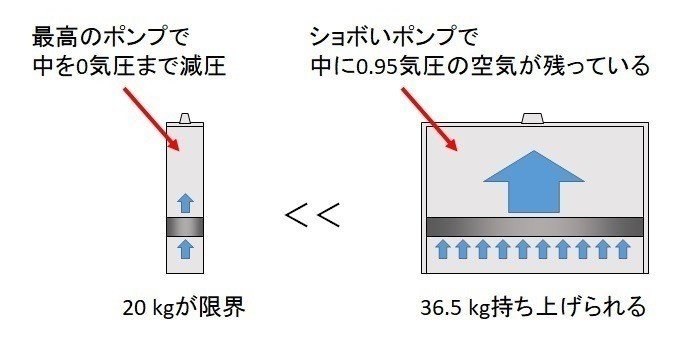
これだとピストンのサイズが30 cmで真空度が5 kPa程度のショボいポンプを使って引いたときの半分程度の力しか出ていません。
ピストンの大きさの重要性がわかりますね。
自社の掃除機の性能にちょうど良いサイズのピストンを準備すれば、凄いパワーがあるように見せられちゃうわけです。
というわけで、こういうパフォーマンスを見たら、なんかインチキ臭いと思ってしまいます…。
掃除機の性能とは直接には関係ないと思っていただいてよいでしょう。
ちなみに余談ですが、「吸引力=大気圧が押す力」ですので、原理上は吸引ポンプで生み出せる圧力差は大気圧が上限ですが、圧縮機(コンプレッサー)は違います。
装置によっては大気圧の数十倍の圧力を実現するものもあります。
大きな物を持ち上げたり、動かしたりする場合に真空ポンプじゃなくてコンプレッサーが使われるのは、そういう理由ですね。
ペットボトルロケットや水鉄砲など、ちょっとしたおもちゃに圧縮空気の技術を応用すれば、驚くようなパワーを発揮してくれますよ。
以上です。
この記事が気に入ったらサポートをしてみませんか?
