Bスプライン完全マスター
参考図書
この文章及びコードは間違いを含んでいる可能性があります。参考図書を良く読んでコードを完璧にし、わたくしに教えてください。
プログラムは最下部、processingです。使用しているソルバーはCommons Mathになります。
スプラインにも色々ある
・普通のスプライン
・Bスプライン
・パラメトリックBスプライン
・NURBS
普通のスプライン
区間ごとに多項式を設定し、それを繋いだもの。そのために一定区間のみ出力する切断べき関数を用いる。ここでは省略する。
Bスプライン
基底関数にBスプライン基底関数を用いたもの。基底関数とは、他の関数の元になりうる関数。係数掛けて足すことで使用される。基底ベクトルみたいな感覚で使っていいかは分からないがそんなようなもの。基底の説明は以下。
データ点、あるいは制御点をN個とする(K-1)次のBスプライン関数は以下の通り。
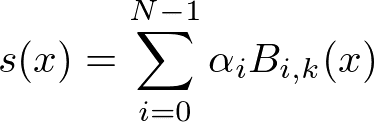
$${\bm \alpha}$$はデータ点、あるいは制御点の座標。
$${\bm \alpha}$$が未知の場合、逆行列を用いて$${\bm \alpha}$$を確定させるスプライン補間関数となる(このページ)。
$${\bm \alpha}$$が既知の場合。グラフィックスにおけるただの制御点である場合、普通に計算するだけである(以下のリンク)。
(K-1)次のBスプライン基底関数の中身は以下の通り。2次スプラインはBi3であり、3次スプラインはBi4である。インデックスのズレに注意。

0次のBスプライン基底関数は以下の通り。インデックスのズレに注意。

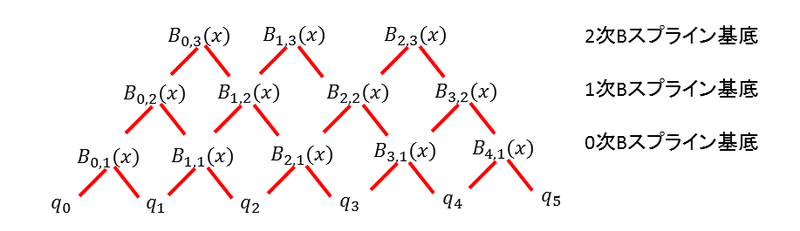
(K-1)次のスプライン関数はN個の(K-1)次Bスプライン基底関数によって構築され、(K-1)次のBスプライン基底関数は各々下位の次数の2つのBスプライン基底関数からなる。最終的に0次のBスプライン基底関数は2つのノットによって定義される。
(K-1)次のBスプライン基底関数がN個あるなら、それを構築するための(K-2)次のBスプライン基底関数が+1個必要。
ノットの個数は0次のBスプライン基底関数+1。
つまりノットの個数を考える際に制御点の個数Nを基準とするならば、次数ごとに基底関数の個数を+1。最後に0次基底関数を構築するためにノットの個数を+1。
従ってN個のデータ点からなる(K-1)次のBスプライン関数は、最低(N+(K-1)+1)=N+K個以上のノットを必要とする。多い分には問題ないが、計算上無意味になる可能性がある。
1次のBスプライン基底関数は2個のBスプライン基底関数と3個のノットから構築される。
2次のBスプライン基底関数は3個のBスプライン基底関数と4個のノットから構築される。
3次のBスプライン基底関数は4個のBスプライン基底関数と5個のノットから構築される。
0次のBスプライン関数
制御点1個、0次のBスプライン基底関数
N=1,K=1,ノット数(N+K)=2
入力xが$${q_0 \leqq x < q_1}$$の時$${B_{0,1}=1}$$であって$${S(x)=\alpha_0}$$
それ以外の時$${S(x)=0}$$
これは例えば$${\bm \alpha_0}$$がベクトルである場合、入力xがノットの範囲内の時のみ存在しえる点。
ノットを$${q_0=0, q_1=1}$$ととるならば、入力xは0~1が適当。それ以外の時、$${\bm \alpha_0}$$は消える。$${B_{i,1}}$$の定義によるが、前述定義の場合は正確にはx=1の時$${\bm \alpha_0}$$は消える。
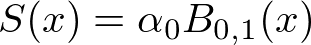

制御点2個、0次のBスプライン基底関数
N=2,K=1,ノット数(N+K)=3
これは例えば$${\bm \alpha_0}$$がベクトルである場合、入力xが各々を構築するノットの範囲内の時のみ存在しえる複数の点。
ノットを$${q_0=0, q_1=1, q_2=2}$$ととるならば、入力xは0~2が適当。
(ただしノットとともに圧縮し、入力xを0~1とすることも可能。その場合全てのノットは入力レンジ2で除される)
入力xが$${0 \leqq x < 1}$$の時$${\bm \alpha_0}$$が現れ、
入力xが$${1 \leqq x < 2}$$の時$${\bm \alpha_1}$$が現れる。
入力x=2の時、正確には$${\bm \alpha_1}$$は消える。
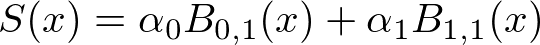

制御点3個、0次のBスプライン基底関数
N=3,K=1,ノット数(N+K)=4


1次のBスプライン関数
制御点1個、1次のBスプライン基底関数
N=1,K=2,ノット数(N+K)=3
ノットを$${q_0=0, q_1=1, q_2=2}$$ととるならば、入力xは0~2が適当。
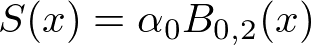
$${B_{0,2}}$$の基底関数は下位の2つの基底関数で構築される。

この場合$${i=0, k=2}$$
$$
B_{0,2}=\frac{x-q_0}{q_1-q_0}B_{0,1}(x)+\frac{q_2-x}{q_2-q_1}B_{1,1}(x)
$$
ここで

であるから、
$${0 \leqq x <1}$$の時
$${B_{0,2}=\frac{x-q_0}{q_1-q_0}B_{0,1}(x)}$$
$${1 \leqq x <2}$$の時
$${B_{0,2}=\frac{q_2-x}{q_2-q_1}B_{1,1}(x)}$$
ノットに単純なものを選んだので、係数部分の分母は常に1。分子はxの範囲と会わせて0~1となる。
ここで入力xを0~2とした場合、出力S(x)は$${0 \leqq x < 1}$$の範囲では原点(0,0)から制御点$${\bm \alpha_0}$$までの軌跡となり、
$${1 \leqq x < 2}$$の範囲では制御点$${\bm \alpha_0}$$から原点(0,0)までの軌跡となる。
これは普通邪魔であるので、xの入力範囲を
$$
knots[d] \leqq x < knots[knots.count-d-1]
$$
とすることで邪魔部分を除去できる。
この場合、除去した結果は入力範囲が$${x=q_1=1}$$となり、制御点$${\bm \alpha_0}$$が出力される。
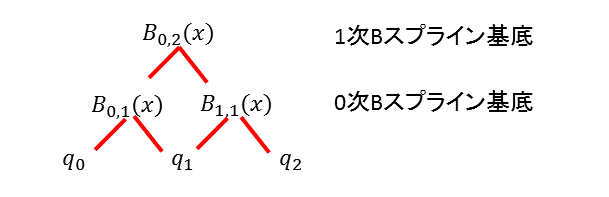
制御点2個、1次のBスプライン基底関数
N=2,K=2,ノット数(N+K)=4
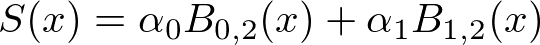

制御点3個、1次のBスプライン基底関数
N=3,K=2,ノット数(N+K)=5


2次のBスプライン関数
制御点1個、2次のBスプライン基底関数
N=1,K=3,ノット数(N+K)=4
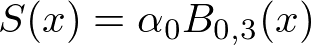

制御点2個、2次のBスプライン基底関数
N=2,K=3,ノット数(N+K)=5
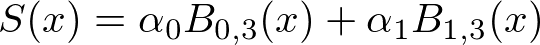

制御点3個、2次のBスプライン基底関数
N=3,K=3,ノット数(N+K)=6

ようやくこの辺から実用的なスプラインになる
ノット
ノットとは単純に増加し、重複を許された数列。
スプライン関数S(x)を用いるうえであらかじめ設定しておかなければならないパラメータである。
元々は曲線の継ぎ目のことであったろうし、多分現在もそういう文脈で使うこともあるであろう。多分。
ノットは1つのデータ点ないし制御点に対して次数に応じた個数分(例えば2次スプラインなら1つの制御点に対して4つ、3次スプラインなら5つ)掛かる、受け持つ。
基底関数の線形和であるスプライン関数S(x)は、ノットベクトル空間を移動するt値を入力に受けると、そのt位置に応じてデータ点ないし制御点から影響を受け、それら全部足して出力とする。この時、入力t値のある領域はノットの効果により無効となり、ゆえにS(x)の入力値xは入力tの部分に限ることが適切となる。
入力t値が1次元ノットベクトル空間を移動するという観点から見れば、ノットベクトルの成分こそがデータ点ないし制御点の勢力圏そのもの。
・節点(Knot)はデータ点(ここではベクトル(x,y))ではない。
・節点はデータ点と一致するわけではない。
・節点はそれなりの条件さえ満たせば適当に決めて良い(シェーンバーグ・ホイットニの条件)p33
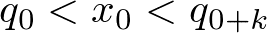
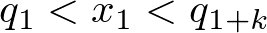
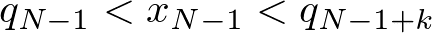
・ノットのインデックスは独立したものであるが、シェーンバーグ・ホイットニの条件を満たすなら個々のデータ点のインデックスにそれなりに関連する。kは関数の次数+1)
・Bスプライン関数はノットさえ設定すれば勝手に動く関数であるが、それを既知のデータ点全域に適用しようと思ったらシェーンバーグ・ホイットニの条件を満たせということである。
パラメトリックでない方のスプラインは以下再掲
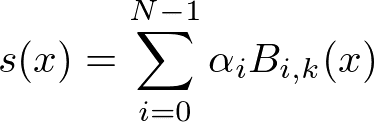
ここで$${\bm \alpha}$$が未知であることに注意が必要。グラフィックス系の文脈で使用されるスプラインは、この$${\bm \alpha}$$がそのままデータ点である。この場合、スプライン曲線は基本的にデータ点を通過しない(例外的にノットを重複させれば通ることは通る)。
$${\bm \alpha}$$が未知であるスプラインは、データ点を用いて連立方程式を解き、$${\bm \alpha}$$を確定させる必要がある。$${\bm \alpha}$$が確定したスプライン曲線はデータ点を通過する。これは補間や近似関数の文脈で利用される。微分方程式を近似的に解く、すなわち親戚は有限要素法とかその辺である。
Bはノットが(あと次数も)決まれば実行可能となる関数。ゆえに既知のデータ点(x,y)を用いればBの出力が定まり、これをN×Nの係数の行列とする。あとはデータ点のyベクトルを用いれば連立方程式を解くための行列計算で$${\bm \alpha}$$ベクトルが求まる。するとS(x)は普通の関数として使用可能となる。このS(x)は補間関数、あるいは近似関数である。
ArrayList<PVector> SplineInterpolation(ArrayList<PVector> vectors, int degree, double accuracy)
{
int N = vectors.size();
int K = degree+1;
double[] knots = make_knots(vectors, degree);
double[][] B = make_Bx(knots,K,vectors);
double[] coeff = make_coefficient_y(B, vectors);
return get_rails(vectors, knots, degree, coeff, accuracy);
//return get_rails_V(vectors, knots, degree, accuracy);
}
//係数を計算し、頂点を通すタイプ
ArrayList<PVector> get_rails(ArrayList<PVector> vectors, double[] knots, int degree, double[] coeff, double accuracy)
{
double sx = vectors.get(0).x;
double ex = vectors.get(vectors.size()-1).x;
double range = ex-sx;
double dx = range*accuracy;
ArrayList<PVector> ret = new ArrayList<PVector>();
ret.add(vectors.get(0).copy());
for(double x = sx; x<ex; x+=dx)
{
ret.add(new PVector((float)x, (float)Sx(vectors, knots, degree, coeff, x)));
}
ret.add(vectors.get(vectors.size()-1).copy());
return ret;
}
//頂点を通らないタイプ
ArrayList<PVector> get_rails_V(ArrayList<PVector> vectors, double[] knots, int degree, double accuracy)
{
double sx = vectors.get(0).x;
double ex = vectors.get(vectors.size()-1).x;
double range = ex-sx;
double dx = range*accuracy;
ArrayList<PVector> ret = new ArrayList<PVector>();
ret.add(vectors.get(0).copy());
for(double x = sx; x<ex; x+=dx)
{
ret.add(Sxv(vectors, knots, degree, x));
}
ret.add(vectors.get(vectors.size()-1).copy());
return ret;
}
//f(x)一回分
double Sx(ArrayList<PVector> vectors, double[] knots, int degree, double[] coeff, double x)
{
int N = vectors.size();
int K = degree+1;
double ret = 0;
for(int i = 0; i<vectors.size(); i++)
{
ret+=coeff[i]*Bik(knots, i, K, x);
}
return ret;
}
//f(x)一回分
//頂点を通らないタイプ
//係数aを求めず、頂点座標をそのまま係数とする
PVector Sxv(ArrayList<PVector> vectors, double[] knots, int degree, double t)
{
int N = vectors.size();
int K = degree+1;
double sumx = 0;
double sumy = 0;
for(int i = 0; i<vectors.size(); i++)
{
PVector v = vectors.get(i);
sumx+=v.x*Bik(knots, i, K, t);
sumy+=v.y*Bik(knots, i, K, t);
}
return new PVector((float)sumx,(float)sumy);
}
double[] make_knots(ArrayList<PVector> vectors, int degree)
{
int N = vectors.size();
int K = degree+1;
double[] q = new double[N+K];
for(int i = 0; i<K; i++)
{
q[i] = vectors.get(0).x;
}
for(int i = 0; i<N-K; i++)
{
q[K+i] = (vectors.get(i).x+vectors.get(i+K).x)/2;
}
for(int i = 0; i<K; i++)
{
q[N+i] = vectors.get(N-1).x;
}
return q;
}
double[][] make_Bx(double[] knots, int k, ArrayList<PVector> vectors)
{
double[][] B = new double[vectors.size()][vectors.size()];
//p35
for(int row = 0; row<B.length; row++)
{
for(int col = 0; col<B[0].length; col++)
{
B[row][col] = Bik(knots, col, k, vectors.get(row).x);
}
}
return B;
}
//vector.yに対する係数β
double[] make_coefficient_y(double[][] B, ArrayList<PVector> vectors)
{
double[] bv = new double[vectors.size()];
for(int i = 0; i<vectors.size(); i++)
{
bv[i]=vectors.get(i).y;
}
double[] ret = solve(B, bv);//solver使用
return ret;
}
//vector.xに対する係数α
double[] make_coefficient_x(double[][] B, ArrayList<PVector> vectors)
{
double[] bv = new double[vectors.size()];
for(int i = 0; i<vectors.size(); i++)
{
bv[i]=vectors.get(i).x;
}
double[] ret = solve(B, bv);//solver使用
return ret;
}
//Bスプライン基底関数
double Bik(double[] knot, int i, int k, double x)
{
//0次B基底
if(k==1)
{
//数学的には
//if(knot[i]<=x&&x<knot[i+1])
//しかしB行列の右下対角に1を格納し、スムーズに行列計算するために<=とした
if(knot[i]<=x&&x<=knot[i+1])
{
return 1;
}
else
{
return 0;
}
}
double al = 0;
if((knot[i+k-1]-knot[i])!=0)
{
al = (x-knot[i])/(knot[i+k-1]-knot[i])*Bik(knot,i,k-1,x);
}
double ar = 0;
if((knot[i+k]-knot[i+1])!=0)
{
ar = (knot[i+k]-x)/(knot[i+k]-knot[i+1])*Bik(knot,i+1,k-1,x);
}
double ret = al+ar;
return ret;
}ソルバ使用
double[] solve(double[][]A, double[]b)
{
double[]x = new double[b.length];
RealMatrix solver_U = exe_solver(A, b);
if(solver_U == null) { return null; }
for(int i = 0; i<x.length; i++)
{
float u = (float)solver_U.getEntry(i, 0);
x[i] = u;
}
return x;
}
boolean is_singlar = false;
RealMatrix exe_solver(double[][]A, double[]b)
{
RealMatrix solver_A = new Array2DRowRealMatrix(A);
RealMatrix solver_b = new Array2DRowRealMatrix(b);
try
{
//特異行列は例外で処理
RealMatrix solver_AI = MatrixUtils.blockInverse(solver_A, 0); //逆行列
RealMatrix solver_u = solver_AI.multiply(solver_b);
is_singlar = false;
return solver_u;
}
catch(SingularMatrixException sme)
{
is_singlar = true;
}
catch(NullPointerException npe)
{
is_singlar = true;
}
catch(MathArithmeticException mae)
{
is_singlar = true;
//ノルムゼロ
}
catch(MaxCountExceededException mcee)
{
is_singlar = true;
//収束失敗
}
return null;
} 他
import org.apache.commons.math3.linear.*;
import org.apache.commons.math3.exception.*;//例外
int window_width = 500;
int window_height = 500;
int ww;
int wh;
PVector pprev;
PVector prev;
PVector current;
PVector dv = new PVector(0,0);
int current_vertex_index = -1;
void mousePressed()
{
pprev = new PVector(mouseX,mouseY);
prev = new PVector(mouseX,mouseY);
current = new PVector(mouseX,mouseY);
for(int i = 0; i<this.vertex.size(); i++)
{
PVector v = vertex.get(i);
if(v.x-r<mouseX&&mouseX<v.x+r)
{
if(v.y-r<mouseY&&mouseY<v.y+r)
{
current_vertex_index = i;
return;
}
}
}
}
void mouseDragged()
{
pprev = prev.copy();
prev = current.copy();
current.x = mouseX;
current.y = mouseY;
dv = PVector.sub(current,prev);
PVector v = this.vertex.get(current_vertex_index);
v.add(dv);
}
void mouseReleased()
{
pprev = null;
prev = null;
current = null;
}
ArrayList<PVector> vertex = new ArrayList<PVector>();
float r = 30;
void settings()
{
size(window_width, window_height);
}
void setup()
{
vertex.add(new PVector(0,100));
vertex.add(new PVector(100,0));
vertex.add(new PVector(200,100));
vertex.add(new PVector(300,0));
vertex.add(new PVector(400,100));
}
void draw()
{
background(255);
DrawLiner(SplineInterpolation(this.vertex, 0, 0.01));
DrawLiner(SplineInterpolation(this.vertex, 1, 0.01));
DrawLiner(SplineInterpolation(this.vertex, 2, 0.01));
DrawLiner(SplineInterpolation(this.vertex, 3, 0.01));
DrawLiner(SplineInterpolation(this.vertex, 4, 0.01));
for(int i = 0; i<this.vertex.size(); i++)
{
PVector v = vertex.get(i);
ellipse(v.x,v.y,r,r);
}
}
void DrawLiner(ArrayList<PVector> vertex)
{
for(int i = 0; i<vertex.size()-1; i++)
{
PVector sv = vertex.get(i);
PVector ev = vertex.get(i+1);
line(sv.x, sv.y, ev.x, ev.y);
}
}この記事が気に入ったらサポートをしてみませんか?
