
行列・線形代数(途中)
この記事はちまちまと逐次更新されうるもので、比較的だろう運転と知ったかぶりが多めです。正確な内容は参考文献をお読みいただけます。
世界標準MIT教科書 ストラング:線形代数イントロダクション
ストラング ギルバート (著), 松崎 公紀 (翻訳), 新妻 弘 (翻訳)
スタンフォード ベクトル・行列からはじめる最適化数学 (KS情報科学専門書) 単行本(ソフトカバー) – ビッグブック, 2021/3/1
ステファン・ボイド (著), リーヴェン・ヴァンデンベルグ (著), 玉木 徹 (翻訳)
行列プログラマー ―Pythonプログラムで学ぶ線形代数 単行本(ソフトカバー) – 2016/10/5
Philip N. Klein (著), 松田 晃一 (翻訳), 弓林 司 (翻訳),
線型代数[改訂版] 単行本 – 2015/3/11
長谷川 浩司 (著)
色々な行列
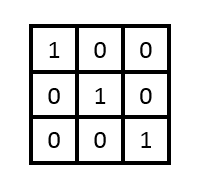
単位行列
対角の要素が1。それ以外が0。
正方行列
行と列の数が同じ行列。
対角行列
正方行列かつ対角要素以外が0の行列。
$$
\begin{pmatrix}
a_{11} & 0 & 0 \\
0 & a_{22} & 0 \\
0 & 0 & a_{33}
\end{pmatrix}
$$
みたいなヤツ
対角行列の行列式は対角成分の積
対角行列の逆行列は各対角要素の逆数を並べたもの。
三角行列
L:下三角行列(左三角行列)
Lower
正方行列かつ
主対角線より上の要素が全て0
$$
\begin{pmatrix}
a_{11} & 0 & 0 \\
a_{21} & a_{22} & 0 \\
a_{31} & a_{32} & a_{33}
\end{pmatrix}
$$
みたいなヤツ
U:上三角行列(右三角行列)
Upper
正方行列かつ
主対角線より下の要素が全て0
$$
\begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
0 & a_{22} & a_{23} \\
0 & 0 & a_{33}
\end{pmatrix}
$$
みたいなヤツ
三角行列の行列式は対角成分の積
逆行列
ある行列に対して積をとると、対象の行列を単位行列化させるような関係にある行列。必ず存在するとは限らず、存在するしないは重要な性質となる。
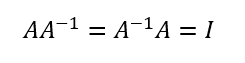
左右で区別する場合があり、
左から引掛けることが可能なら左逆行列。
右から引掛けることが可能なら右逆行列。
疑似逆行列
左逆行列を持つ行列の列は線形独立である。
行列Aの列が線形独立であれば左逆行列を持つ。
Aが線形独立の時$${A^TA}$$は正則。逆行列を持つ。
$${((A^TA)^{-1}A^T)A=(A^TA)^{-1}(A^TA)=I}$$
ここで$${(A^TA)^{-1}A^T}$$はAの左逆行列。
また、この形の左逆行列を疑似逆行列という。
$$
A^{\dagger} = (A^TA)^{-1}A^T
$$
正則行列
逆行列が存在する行列。
左逆行列が存在すれば左正則。
右逆行列が存在すれば右正則。
転置
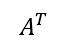
m*n行列の行indexと列indexを入れ替えたもの。出力はn*m行列。
//C#
public static double[,] Transposition(double[,] matrix)
{
int m = matrix.GetLength(0);
int n = matrix.GetLength(1);
double[,] ret = new double[n, m] ;
for (int i = 0; i <m ; i++)
{
for (int j = 0; j <n; j++)
{
ret[j, i] = matrix[i, j];
}
}
return ret;
} 転置の性質
wikipediaより
対合性
転置の転置は元の行列
$${A^{TT}=A}$$
加法性
和の転置は転置の和
$${(A+B)^T=A^T+B^T}$$
斉次性
係数倍の転置は転置の係数倍
$${(kA)^T}$$=kA^T
線形性(加法性+斉次性)
$${(kA+lB)^T=kA^T+lB^T}$$
積の転置は左右入れ替えた転置の積
$${(AB)^T=B^TA^T}$$
対称行列
転置しても変わらない行列。
転置=元の行列。
その定義から必ず正方行列(行数=列数)。
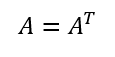
$$
A=
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots\\
a_{n1}& a_{n2} & \cdots & a_{nn} \\
\end{pmatrix}
$$
である時、$${a_{ij}=a_{ji}}$$なもの。
固有値も固有ベクトルも全て実数。
固有ベクトルは互いに直交する。
直交行列
転置=元の行列の逆行列。
正方行列。正則行列。
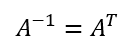
エルミート転置
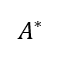
随伴行列、エルミート共軛(きょうやく)、エルミート随伴。
転置のパワーアップ。
複素数を成分にもつ行列に付いて、転置してから複素共軛(虚部の符号を反転)をとるもの。
エルミート行列
自己随伴行列。
対称行列のパワーアップ。
エルミート転置=元の行列。
複素正方行列。
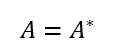
ユニタリ行列
直交行列のパワーアップ。
エルミート転置=元の行列の逆行列。
複素正方行列。正則行列。
ヘッセ行列
p347
統計のための行列代数 上 単行本(ソフトカバー) – 2012/4/5
D. A. ハーヴィル (著)
ベクトルを入力にとり、スカラーを出力する関数の高階微分。
ベクトルを入力にとり、スカラーを出力する関数の1階微分は勾配。
$$
H(f)_{ij}(\bm x)=\nabla_i\nabla_jf(\bm x)=\frac{\partial^2}{\partial x_i \partial x_j}f(\bm x)
$$
$$
H(f)
=\begin{bmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n}\\
\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2\partial x_n}\\
\vdots &\vdots & \ddots & \vdots\\
\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2}\\
\end{bmatrix}
$$
ヤコビ行列
ベクトル場をベクトルで微分したもの
$${\bm y = (y_1, y_2, …, y_m)}$$
$${\bm x = (x_1, x_2, …, x_n)}$$
これをヤコビ行列という。
m=1の時、勾配の転置に一致。
p470
スタンフォード ベクトル・行列からはじめる最適化数学 (KS情報科学専門書) 単行本(ソフトカバー) – ビッグブック, 2021/3/1
ステファン・ボイド (著), リーヴェン・ヴァンデンベルグ (著), 玉木 徹 (翻訳)
$$
\frac{\partial \bm y}{\partial \bm x}
=\begin{bmatrix}
\frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_n}\\
\frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \cdots & \frac{\partial y_2}{\partial x_n}\\
\vdots &\vdots & \ddots & \vdots\\
\frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \cdots & \frac{\partial y_m}{\partial x_n}\\
\end{bmatrix}
$$
グラム行列
p195, P233
スタンフォード ベクトル・行列からはじめる最適化数学 (KS情報科学専門書) 単行本(ソフトカバー) – ビッグブック, 2021/3/1
ステファン・ボイド (著), リーヴェン・ヴァンデンベルグ (著), 玉木 徹 (翻訳)
Aをm*n行列、その列を$${a_1,…a_n}$$とする。
$${G=A^TA}$$なる行列Gをグラム行列という。
$$
A=
\begin{bmatrix}
\bm a_1 & \bm a_2 & \cdots & \bm a_n\\
\end{bmatrix}
$$
行列の積をとると、
その出力となる行列の各要素は、
行ベクトルと列ベクトルの内積となる
$${A^TA}$$の場合、その各要素は
$${A^T}$$の行ベクトルと
$${A}$$の列ベクトルとの内積
$$
G=A^TA=
\begin{bmatrix}
\bm a_1^T\bm a_1 & \bm a_1^T\bm a_2 & \cdots & \bm a_1^T\bm a_n\\
\bm a_2^T\bm a_1 & \bm a_2^T\bm a_2 & \cdots & \bm a_2^T\bm a_n\\
\vdots &\vdots &\ddots & \vdots\\
\bm a_n^T\bm a_1 &\bm a_n^T\bm a_2 &\cdots &\bm a_n^T\bm a_n
\end{bmatrix}
$$
m*n行列Aの各列が線形独立ならn*nグラム行列$${A^TA}$$は正則。
かつ、正則ならAの各列は線形独立。
Vandermonde行列
ChatGPT4
Vandermonde行列は、線形代数学の特定の行列の一つで、以下のように定義されます。
与えられたベクトル $${ \mathbf{v} = [v_1, v_2, \ldots, v_n] }$$ に対して、Vandermonde行列 ( V ) は次のように構築されます:
$$
V = \begin{pmatrix}
1 & v_1 & v_1^2 & \cdots & v_1^{n-1} \\
1 & v_2 & v_2^2 & \cdots & v_2^{n-1} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & v_n & v_n^2 & \cdots & v_n^{n-1} \\
\end{pmatrix}
$$
この行列の特徴は、各行がベクトルの要素の連続したべき乗で構成されていることです。Vandermonde行列は、多項式補間や多項式回帰分析など、様々な応用分野で利用されます。
特に、Vandermonde行列の行列式は、ベクトルの要素の差の積として計算することができます。具体的には、
$$
\det(V) = \prod_{1 \leq i < j \leq n} (v_j - v_i)
$$
Vandermonde行列の主な問題点は、条件数が非常に大きくなる可能性があるため、数値的に不安定になることがあります。そのため、実際の計算でVandermonde行列を直接使う場合は注意が必要です。
ラグランジュ補間:
Vandermonde行列とラグランジュ補間は、多項式補間の文脈で密接に関連しています。以下にその関係を詳述します。
ラグランジュ補間は、与えられた点集合 $${ (x_0, y_0), (x_1, y_1), \ldots, (x_{n-1}, y_{n-1}) }$$ に基づいて、その点を通る多項式を求める方法です。
この補間多項式 ( P(x) ) は以下のように表されます:
$${ P(x) = \sum_{i=0}^{n-1} y_i L_i(x) }$$
ここで、( L_i(x) ) はラグランジュ基底関数で、以下のように定義されます:
$${ L_i(x) = \prod_{j=0, j\neq i}^{n-1} \frac{x - x_j}{x_i - x_j} }$$
Vandermonde行列との関係:
Vandermonde行列を使用して、同じ点集合に基づく補間多項式の係数を求めることができます。具体的には、Vandermonde行列 ( V ) は次のように定義されます:
$$
V = \begin{pmatrix}
1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\
1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^{n-1}
\end{pmatrix}
$$
ある補間多項式 $${ P(x) = a_0 + a_1 x + a_2 x^2 + \ldots + a_{n-1} x^{n-1} }$$があるとき、その係数ベクトル $${ \mathbf{a} }$$ は次のように求めることができます:
$${ V \mathbf{a} = \mathbf{y} }$$
ここで、( \mathbf{y} ) は与えられたy値を含むベクトルです。この方程式を解くと、多項式の係数を得ることができます。
このアプローチの限界は、Vandermonde行列が数値的に不安定になることがあるという点です。そのため、大きな次数の補間問題に対して、この方法で直接Vandermonde行列を使用することは推奨されません。
しかし、Vandermondeのアプローチとラグランジュ補間は本質的に同じ問題を解決しています:与えられた点を通る多項式を見つけること。これらの方法は異なる観点からこの問題にアプローチしており、それぞれの方法には利点と欠点があります。
Toeplitz行列
ChatGPT4
Toeplitz行列は、線形代数学における特定の形の行列で、各対角線上の要素が一定です。具体的には、任意の( i, j )に対して、行列の( i, j )要素は、( i - j )の差にのみ依存します。
与えられたベクトル $${ c = [c_0, c_1, \ldots, c_{n-1}] }$$ および $${ r = [r_0, r_1, \ldots, r_{n-1}] }$$ を使って、$${ n \times n }$$ Toeplitz行列 $${ T }$$ は次のように表現されます:
$$
T = \begin{pmatrix}
c_0 & r_1 & r_2 & \cdots & r_{n-1} \\
c_1 & c_0 & r_1 & \cdots & r_{n-2} \\
c_2 & c_1 & c_0 & \ddots & \vdots \\
\vdots & \ddots & \ddots & \ddots & r_1 \\
c_{n-1} & \cdots & c_2 & c_1 & c_0 \\
\end{pmatrix}
$$
この定義では、第一列はベクトル ( c ) から取られ、第一行はベクトル ( r ) から取られます。
Toeplitz行列は、時系列分析、信号処理、および通信の分野でしばしば登場します。特に、自己相関関数が等しいと仮定される信号の畳み込みに関連する線形方程式を表現するのに便利です。
Toeplitz行列の魅力的な特性の一つは、その構造を利用して行列ベクトルの乗算や、線形方程式の解法などの計算を効率的に行うことができる点です。
Hilbert行列
Hilbert行列は、数値解析の分野でよく知られている特定の形の正方行列です。その名前は、ドイツの数学者デイヴィッド・ヒルベルトにちなんで名付けられました。Hilbert行列は、その成分が以下のように与えられるものです:
$$
H_{ij} = \frac{1}{{i + j - 1}}
$$
したがって、$${ n \times n }$$のHilbert行列は以下のようになります:
$$
H = \begin{pmatrix}
1 & \frac{1}{2} & \frac{1}{3} & \cdots \\
\frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \cdots \\
\frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \cdots \\
\vdots & \vdots & \vdots & \ddots \\
\end{pmatrix}
$$
Hilbert行列は、数値的に非常に不安定です。この行列の条件数は非常に大きく、それにより小さな入力の変化が出力の大きな変化を引き起こす可能性があります。このため、Hilbert行列を扱う際の計算やその逆行列を直接使うのは一般的に避けられます。
Hilbert行列とその逆行列の成分は、連分数や連続分数展開と関係があります。また、Hilbert行列は最小二乗問題や積分方程式の数値的解法の文脈で研究されることもあります。
数値解析の教材や講義では、Hilbert行列が数値計算の困難さや計算の安定性を説明する例としてしばしば引用されます。
行列式
行列式がゼロだと逆行列は存在しない。
対角行列の行列式は対角成分の積
三角行列の行列式は対角成分の積
ヘシアン
ヘッセ行列の行列式
ヤコビアン
ヤコビ行列の行列式
線形写像(線形変換、1次変換)
以下の線形性を満たす写像、変換。
線形性
$${\mathbb R^n}$$の全てのベクトルと
全てのスカラーcに関して以下のような操作ができること。
加法性
$${f(\mathbf x_1+\mathbf x_2)=f(\mathbf x_1)+f(\mathbf x_2)}$$
斉次性
$${f(c\mathbf x)=cf(\mathbf x)}$$
写像
行列Aは(標準基底とは限らない)正規直交ベクトルの組を、別のベクトルの組(像)にうつす。この時の行列Aは写像としての役割を持つ。
正規:(ベクトルの)長さ1
直交ベクトル:内積すると0のベクトルら
標準基底:例えば(1,0)(0,1), (1,0,0)(0,1,0)(0,0,1) など
基底:->https://note.com/alchan/n/n2b42708ca6d1
言葉を換えれば、行列Aからは正規直交ベクトルの組をひっこぬくことができる。ぬきだす正規直交ベクトルの値によってうつされるベクトルの組も変わる。
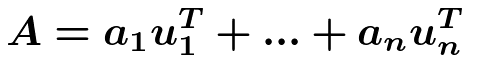
例えば
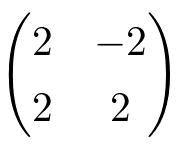
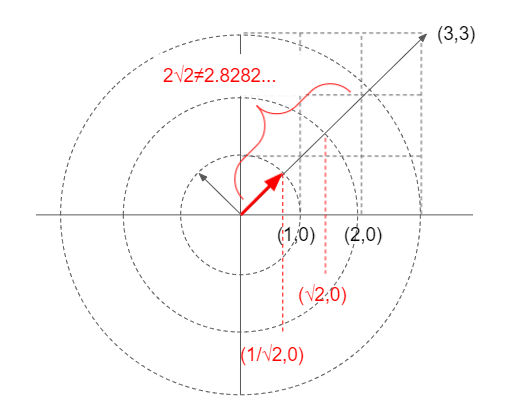
なる行列Aがあるとすると、この行列は正規標準基底(1,0)を(2,2)に、(0,1)を(-2,2)にうつす。
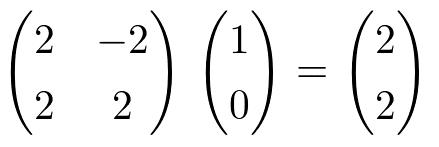
正規標準基底を45度傾けた基底(1/√2,1/√2,)(-1/√2,1/√2)を考えたとき、この基底が各々(2,2),(-2,2)にうつされることを考えると、この時の写像となる行列Aは
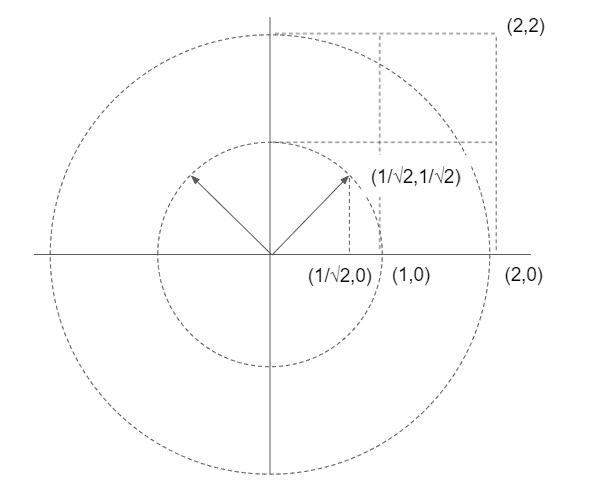

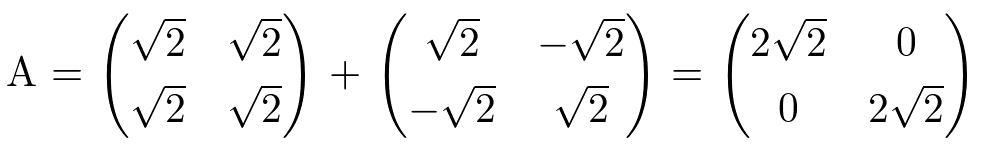
この行列A
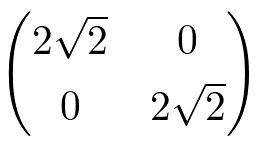
は、基底(1/√2,1/√2)(-1/√2,1/√2)を、各々(2,2)(-2,2)にうつす。
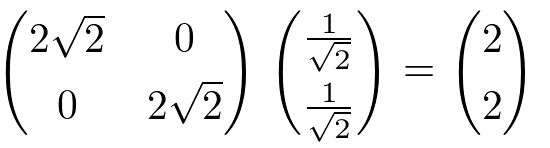
正規標準基底の1つ(1,0)からみて(2,2)の位置にある座標は、とある正規直交基底の1つ(1/√2,1/√2)からみると(2/√2,0)の位置にある。
正規標準基底の1つ(0,1)からみて(-2,2)の位置にある座標は、とある正規直交基底の1つ(-1/√2,1/√2)からみると(0,2/√2)の位置にある。
行列Aは基底と、基底が行列Aによってうつされた像の組から構築される。行列Aからは基底をひっこぬくことができる。
ある座標を別の座標系から見たい場合、みたいな話は座標変換の話になって、微妙に意味が違う。
線型方程式
連立方程式の組があるとして

その係数は
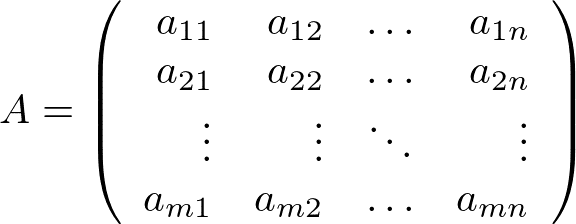
行列及びベクトルにまとめると
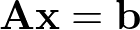
この時、xが既知でbが未知なる問題を準問題。bが既知でxが未知なる問題を逆問題という。
準問題は行列の積を求めればよい。逆問題を解くには以下の形式
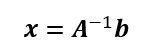
を解くことになる。そのためには
強引に逆行列を求める場合
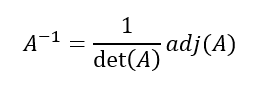
ここで余因子展開やら行列式やらの説明の必要があるが、wikipediaか下部リンクを参照。
基本的に逆行列を公式に基づいて求めることは4*4行列くらいまでが限界である。また、なんらかの効率的な方法に基づいて逆行列を生成したとしても、それを用いて行列の積をとるという手法(直接法)はやはりあんまり効率的でない。
そのまま強引に解いちゃう(クラメルの公式)
公式に基づいてそのまま連立方程式を解いてしまう公式。そのまま実装すると効率は最も悪い。ただし、実装によってはガウスの消去法並みになるとの記述がwikipediaとその引用論文にある。
ガウスの消去法、ガウスジョルダン法などを用いる
手で、ないしコンピューターで行列を演算する上で、基本というか土台となる手法。行ごとに操作していく途中で除算を用いるが、その際に分母がゼロかつ、他の行と交換してみてもやっぱりゼロならば行列は正則ではなかった(連立方程式は解けない、行列式はゼロ)とみなされる。
つまり連立方程式が解けるかどうかの判定はとりあえずやってみんと分からんということである。
行交換のことを部分ピボット交換といい、これはなかば必須の操作である。列まで交換する完全ピボットというものもあるが、これは数値計算上の精度を高める目的で使用されるだけで、必須ではない。計算が解けなくてもいいから分解だけでもやり切りたい等の時も使う模様。
連立方程式を解くのが基本であるが、逆行列を求める、行列式を求める、ランクを求める、正則判定などの操作に発展する。
行列を他の形に変形(分解)してから解く
基本的にはこれらの手法に頼ることになる。計算が早くなるだけでなく、数値的に安定することもある。また、手法によって操作対象となる行列に制限が付いたり、逆に緩んだりする。
LU分解、QR分解、コレスキ分解、SVD(特異値分解)などがある。
多項式と微分方程式の次数
線形形式
線形写像の1つ。
次数1の同次多項式。
$$
f(\mathbf x)=\bm a^T\mathbf x=\sum_ia_ix_i=(\bm a, \mathbf x)
$$
$$
\bm a^T\mathbf x = \mathbf x^T \bm a
$$
ここで例えば$${\mathbf x=(x,y)}$$ならば
$${f(x,y)=a_1x+a_2y}$$である。
$${\mathbf x=(x,y,z)}$$ならば
$${f(x,y,z)=a_1x+a_2y+a_3z}$$である。
二次形式
次数2の方程式までは線形代数でいける。
$$
q(x,y)=ax^2+bxy+cy^2=
\begin{bmatrix}
x & y
\end{bmatrix}
\begin{bmatrix}
a & \frac{b}{2}\\
\frac{b}{2} & c
\end{bmatrix}
\begin{bmatrix}
x\\
y
\end{bmatrix}
$$
あるいは
$$
q(x,y)=ax^2+bxy+cy^2
q(x,y,z)=ax^2+by^2+cz^2+dxy+exz+fyz
$$
みたいなやつ。
各項の変数の次数の合計をもって項の次数とし、
最も大きい項の次数を式の次数とする。
また、二次形式であるためには斉次(同次)形でなければならず、
斉次(同次)であるとは、各項の次数が同じであることである。
$$
q(x,y)=ax^2+bxy+cy^2+d
q(x,y)=ax^2+bx+c
$$
は斉次(同次)でないので二次形式ではない。
一般化すると
$$
f(\mathbf x)=\sum\limits_{i,j=1}^Na_{i,j}x_ix_j \quad(a_{ij}=a_{ji})=(\mathbf x, A \mathbf x)
$$
ここで$${\bm A}$$は対象行列。
双線形形式
次数2の同時多項式。
$${\mathbf x}$$の要素を固定すると$${\mathbf y}$$に関する一次の同時式となり、$${\mathbf y}$$の要素を固定すると$${\mathbf x}$$に関する一次の同時式となる。
$${A=a_{ij}}$$をm*n行列として、
$${\mathbf x =(x_1,…,x_m)^T}$$と
$${\mathbf y =(y_1,…,y_m)^T}$$に関して
$$
f(\mathbf x, \mathbf y)=\mathbf x^T A \mathbf y=\sum_{i,j}a_{ij}x_iy_j=(\mathbf x, A\mathbf y)
$$
なる形式の関数。
また
$$
\mathbf x^T A \mathbf y=\mathbf y^T A^T \mathbf x
$$
零空間
ストラング青p138
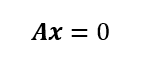
の全ての解なるxベクトルからなる空間。この零空間上にあるxベクトルは行列Aの全ての行に対して直交する。
(a11*a12*a13)*(x1,x2,x3)=0
(a21*a22*a23)*(x1,x2,x3)=0
(a31*a32*a33)*(x1,x2,x3)=0
射影行列:直線に落とす場合
ストラング青p218
あるベクトルbの射影ベクトルをpとした時、Pb=pなるPを射影行列。
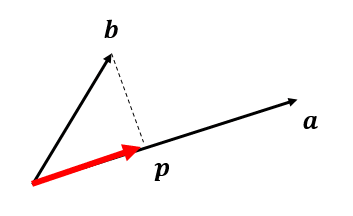
図から以下の関係が立つ。kは適当な係数。

適当な係数k及び射影ベクトルは以下のようになる。
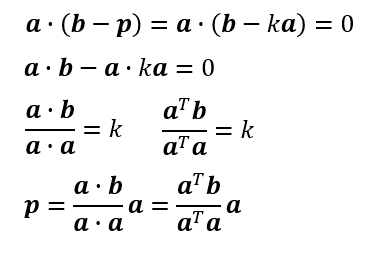
a・b->a^Tb : 内積は行列の積に変換できる
求めたいのは
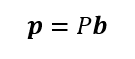
なるを満たす行列Pであるから
p:射影ベクトル
P:射影行列
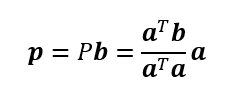
bを落としたいので係数の塊である内に右によせておく

ゆえに射影行列Pは
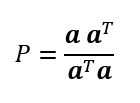
aが単位ベクトルならa・a=a^Taは1
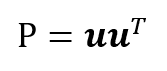
これは写像のとこの
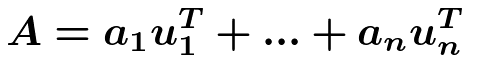
の右辺第一項のみぶんどったものに相当。あとは直交補空間の項を参照。
ベクトルはこの辺も参照
射影行列:平面に落とす場合
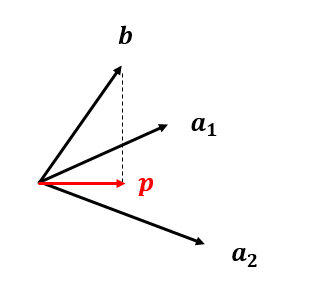
この時平面上の射影ベクトルpは
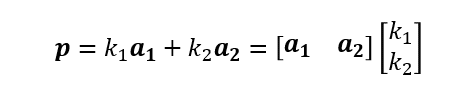
例によって垂直射影ベクトルとは直交する。
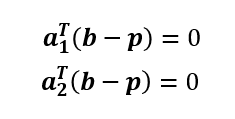
ここで
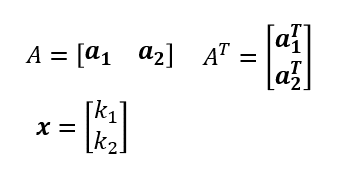
とおくと
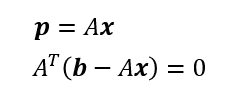
ここから
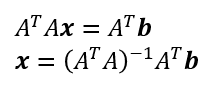
であるから、射影ベクトルは
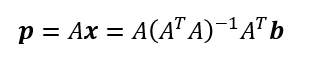
ベクトルbを射影ベクトルpに射影する射影行列Pは
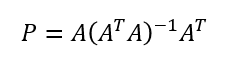
ここで
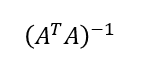
が存在するのはAの全ての列が独立である時のみ。A自体は正則(逆行列を持つ)である必要も無ければ正方行列(行数=列数)である必要も無いm*nの矩形行列。また

はグラム行列。グラム行列は対称行列。(スタンフォードp195)
対称行列は自身と転置が一致する正方行列(行数=列数)。
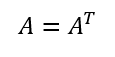
なるもの。つまりグラム行列は転置しても元の行列と一致する正方行列(行数=列数)。Aがm*nならばグラム行列はn*nの正方行列(行数=列数)。
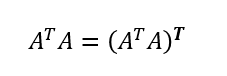
グラム行列自体は対称行列ではあるが、必ずしも正則ではないので逆行列を持つとは限らないが、Aの全ての列が線形独立(各々のベクトルが零ベクトルでなく、かつ他のベクトルの和で表されることがない基底足りえる関係にある)ならそのAの成すグラム行列は逆行列を持つ正則行列かつ対称行列。(多分)
また、射影行列
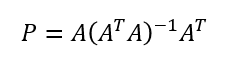
は対象行列である。また、2回乗ずると元に戻る(べき等)
線形代数セミナーp7
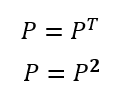
直交補空間
ある空間がいくらかの線形独立のベクトルから構築されるのであれば、その空間を成す線形独立なベクトルの総数以下の個数の線形独立ベクトルから構築される空間は部分空間。
例えば最初に3次元空間を想定するなら、その空間中に想定される面や線はだいたい部分空間。部分空間として面を張る(基底に対して係数掛けて足す)には線形独立なベクトルが2つ必要であり、線を張るには線形独立なベクトルが1つ必要となる。ただ1つのベクトルはだいたいにおいて線形独立であるが、零ベクトルは線形独立ではない。
部分空間として面を張ったならその直交補空間は線である。線を張ったなら面である。ちゃんとした定義は教科書を見なければならない。
ある部分空間に射影行列を用いてベクトルを焼き付けるなら、その部分空間に対する直交補空間にベクトルを焼き付けるための射影行列も存在する。
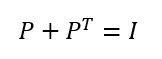
原点を通る単位ベクトルuを考えた時、その単位ベクトル方向に張られる1次元部分空間(線)に焼き付ける作用をもつ射影行列は
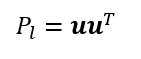
これは上の方の直線に焼き付けるための射影行列(a=u)、あるいは一般化された射影行列の式からも求められる。この時の直交補空間は2次元部分空間の面となり、その面に焼き付けるための射影行列はその面の単位法線ベクトルをもって
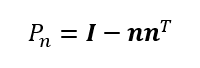
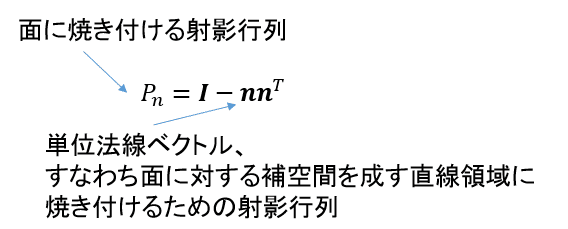
と示される。この形式はグラムシュミット法に発展する。
グラムシュミット法
グラムシュミット法のプログラム的な話はこちら
直和分解
ある空間のとあるベクトルを、部分空間への射影と、その反射影ベクトルの和に分解することを、部分空間とその直交補空間への直和分解という。
固有値・固有ベクトル
固有値と固有ベクトルとは
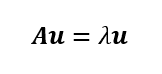
なるベクトルu(固有ベクトル)、スカラーλ(固有値)。u≠0。
対称行列(転置しても変わらん)のすべての固有値は実数。
異なる固有値に対応する固有ベクトルは互いに直交する。
普通、ベクトルは行列に引っ掛けたら回転したり反転したりぐるぐると変形されるが、それらの行列由来の変形がたかだか定数倍で済んでしまうベクトルがある。伸び縮みで済んでしまうベクトルがある。そういう特別なベクトル、それに対応する特別な値が『行列毎に』だいたいある。それが固有値、固有ベクトル。
これらを求めるためには
固有方程式、固有多程式、特性方程式、特性多項式
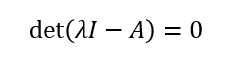
を解く。手でやる、あるいは強引にやる場合は行列式をそのまま解く。数値的、プログラム的、可能な限り高速に実行するにはいくらかのアルゴリズムを用いる。
ガウスの消去法
行列の形に格納された連立方程式をアルゴリズム的に解く方法。
LU分解やQR分解は、アルゴリズムの実行速度、数値的安定性のために用いられる。特異値分解は正方行列でない行列にも適用可能で、なにやってんのか良く分からないことを除けば基本的には特異値分解で良い。
LU分解
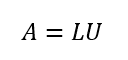
基本的には正方行列を下三角行列Lと上三角行列Uに分解する。ただし長方形行列に一般化することもできる(wiki)。ガウスの消去法時、適時記録していくとそのまま作成できる。ある意味で機械化され、パッケージ化されたガウスの消去法こそがLU分解である。
ガウスの消去法の親戚であるので、とりあえず分解してみんことには分解できるかどうか分からんタイプである。
Lの対角が1だとドリトル法、Uの対角が1だとクラウト法。対角要素だけ引っこ抜くと
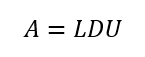
となってLDU分解と称される。Dは対角要素以外が0である対角行列。また、Dの対角要素は必ずしも1ではない。LとUの対角要素はどちらも1となる。
Aが正則ならば、つまり分解してみて分解できちゃったならLDU分解は一意である。また、LDU分解が存在するならばその時のLとUも一意である。ということはLU分解というのは対角要素をどこに押し付けるか程度のブレがあるだけで、Dの扱いさえ定まれば一意であるであろうと思われる。この辺のことは英語wikipediaを鵜呑みにした上での勝手な感想である。
一意であるとは一通りであるということで、ある行列Aを定まったルールの範囲内、行列の求めたい性質を破壊しない範囲で変形を繰り返してみて、結果例えばLが形成されたなら残りかすでUもできてるよという話に繋がるが、その辺りのことを精密に説明する能力は著者にはない。
LU分解時、部分ピボットする場合はLUP分解とも呼ばれ
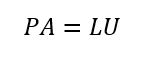
で表される。Pは行を並べ替えるための行列。列も交換するなら
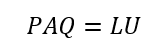
で表される。ただしQは列を交換する行列であって、QR分解とは関係ない。
QR分解
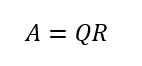
QR分解は、正規方程式を解いたり(最小二乗法)、固有多程式を解いたり(固有値問題)するのに便利なように行列を分解する。
Aは実数ないし複素数の正方行列(ただし長方形行列に一般化できる)。QはAが実数なら直交行列。Aが複素数ならユニタリ行列。Rは上三角行列。
直交行列は転置と逆行列が一致する正方行列。
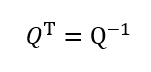
なので転置と積をとると単位行列になる
$$
Q^TQ=QQ^T=I
$$
Aが正則かつRの対角要素が正の場合、この分解は一意である。負が混じるならQはユニタリ行列である。
分解のための方法はグラムシュミット法、ハウスホルダー変換が代表される。ギブンス回転でもいける(wiki)。
QR分解からは連立方程式が解けます。(スタンフォードp226)
QR分解からは行列式、逆行列が求められます。
QR分解からは固有値・固有ベクトルが求められます。(QR法)
QR分解からは最小二乗法も解けます。(スタンフォードp252)
QR分解からは疑似逆行列(一般逆行列)も作れます。(スタンフォードp234)
最小二乗法への適用
$$
A\bm x=\bm b
$$
がある時
$${A\bm x - \bm b}$$を残差
そのノルムを$${||A\bm x - \bm b||}$$とする時、
その最小化を考える
ノルムの最小化とノルムの2乗の最小化は同じことなので計算のために2乗する。
$$
f(\bm x)=||A\bm x - \bm b||^2
$$
この関数の勾配が0になれば最小値であるから
$$
\nabla f(\bm x)=2A^T(A\bm x - \bm b)
$$
正規方程式は
$$
A^TA\bm x= A^T\bm b
$$
ここで$${A^TA}$$はグラム行列。
Aの列が線形独立ならばグラム行列は正則。よって解は
$$
\bm x = (A^TA)^{-1}A^T\bm b
$$
ここで$${(A^TA)^{-1}A^T}$$は疑似逆行列。よって式は
$$
\bm x = A^\dagger\bm b
$$
対角化
$${A}$$を対称行列。
その固有値を$${\lambda_1,…,\lambda_n}$$
その固有値に対応する固有ベクトルを列とする行列を
$${\bm U = (\bm{u_1…u_n})}$$
とする時
$$
\bm{U^TAU}=
\begin{pmatrix}
\lambda_1 & & & \\
& \lambda_2 & & \\
& & \ddots & \\
& & & \lambda_n\\
\end{pmatrix}
=\bm{D}
$$
なる関係性、および操作。
$${\bm u}$$が固有ベクトルである時、
$$
A\bm u=\lambda \bm u \quad (\bm u \neq \bm 0)\\
A\bm u - \lambda \bm u = \bm 0
$$
だから$${A=\begin{bmatrix}a & b\\c & d\end{bmatrix}}$$とすると
$$
\begin{bmatrix}a & b\\c & d\end{bmatrix} \bm u-
\begin{bmatrix}\lambda & 0\\0 & \lambda \end{bmatrix} \bm u
=
\lbrace A-\lambda I \rbrace \bm u
=
\begin{bmatrix}a-\lambda & b\\c & d-\lambda\end{bmatrix} \bm u
=\bm 0
$$
ここで$${\begin{bmatrix}a-\lambda & b\\c & d-\lambda\end{bmatrix}}$$が逆行列を持つと$${\bm u = \bm 0}$$が成立してしまうが、固有ベクトルの定義上そうなってはならない。
ゆえに$${\begin{bmatrix}a-\lambda & b\\c & d-\lambda\end{bmatrix}}$$は逆行列をもってはならず、逆行列をもたないということはその行列式は0でなければならない。よって固有値が満たすべき固有方程式は、
固有方程式
$$
det(A-\lambda I )
=
\begin{vmatrix}
a-\lambda & b\\
c & d-\lambda
\end{vmatrix}
=
(a-\lambda)(d-\lambda)-bc=\lambda^2-(a+d)\lambda+(ad-bc)=0
$$
この方程式は複素数の範囲で必ず解$${\lambda}$$を持つ。
2次正方行列は固有方程式が重根を持たない限り必ず対角化できる。
スペクトル分解(固有値分解)
$$
\bm A = \bm{UDU^{-1}}
$$
SVD(特異値分解)
m*n行列Aにおいて
m次ベクトルuを左特異ベクトル
n次ベクトルvを右特異ベクトル
左特異ベクトルuはm*m対称行列AA^Tの固有ベクトル
右特異ベクトルvはn*n対称行列A^TAの固有ベクトル
σは特異値
σ^2は固有値
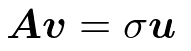
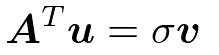
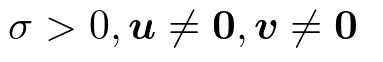
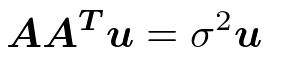
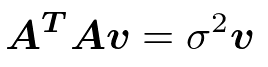
この記事が気に入ったらサポートをしてみませんか?
