補間、および線形性

アルちゃん

2020年11月14日 14:44

このページは書きかけであるが、出先からちょくちょく確認するためにここに公開される。

基底

・ベクトルは２つ足すと別のベクトルになる。

・ベクトルは定数倍すると伸び縮みする。

たいがいのベクトルは、基準となるベクトルに係数を掛け、それらを足し合わせることで表現できる。その時、基準となるベクトルのことを基底という。

基底は基本的には適当に決めて良いが、最も標準的な基底のことを標準基底という。例えば２次元空間ならば(1,0)(0,1)なる２つのベクトル。３次元ベクトルなら(1,0,0)(0,1,0)(0,0,1)なる３つのベクトルが標準基底にあたる。

基底のちゃんとした定義はwikipediaに書いてあるが

なるを満たすに、全てのaがゼロでなければ成立しないようなベクトルのことを線形独立といい、基底とはそれの集まりである。

で、あるからして。基底であることと直交している（内積ゼロ）とか、長さが１とかとは別の話である。標準基底は正規直交基底（長さ１、内積ゼロ、互いに独立）である。

この基底の独立性というのがどれくらいの縛りかといえば、例えば二次元空間はただの２つの二次元基底ベクトルをこねくり回すことだけで表現することが可能になるが、逆にどれだけこねくり回しても三次元ベクトルは構築できないというレベルの縛りである。

線形性

$${\mathbb R^n}$$の全てのベクトルと
全てのスカラーcに関して以下のような操作ができること。

加法性
$${f(\mathbf x_1+\mathbf x_2)=f(\mathbf x_1)+f(\mathbf x_2)}$$

斉次性
$${f(c\mathbf x)=cf(\mathbf x)}$$

直交性

上の図Aの場合、ベクトル(1,0)とベクトル(1,1)は内積すると1。つまり直交してない。
式(1.0)はa1,a2,a3…を組としてベクトル（ないし1行or1列の行列)
v1,v2,v3…の各ベクトルを組としてベクトル（ないし1行or1列の行列)
を成せばこれらの積の総和（内積）の結果は０であるから直交している。
数値であるとかベクトルであるとか、関数であるとかは抽象化され、それらの組み合わせや変換の規則の方がよっぽど問題になる。その一つの例が内積。

また、区間[a,b]において区分的に連続な実数値関数f(x),g(x)がある時、

$$
(f,g)=\int_a^bf(x)g(x)dx
$$

をf(x)とg(x)の内積という。これはフーリエ級数とかで出てくる。

線形独立と線形結合

他を生み出す基準となるようなものに係数掛けて全部足せば他の大体のもんは生成できる。こんなようなことは関数でもできる。すなわち他の基準となるような関数に係数掛けて足せば、他の大体の関数は表現できる。こんなような要領のことごとを線形結合という。

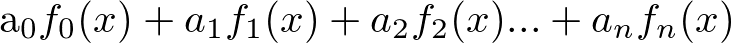
よく使われるのが以下の多項式(polynomial)

あるいは三角多項式(trigonometric polynomial)

微分方程式の場合、道関数yとその導関数

についての1次式

なるをn階1次の線形微分方程式という。
とくにQ(x)=0の時を斉次（同次）という。
Q(x)≠0の時、Q(x)の項の次数が0なので斉次にならない（と、思われる）。
物理的には保存則（微分=0、ゆえに量の変化なし）に相当。
Q(x)≠0の時、系に外力が加わっている状態。

次数と斉次（同時）

補間

補間というのは、情報が足らない時に、その情報のスキマを関数で埋めてしまうことである。

例えば１００×１００ピクセルの画像を２００×２００ピクセルに拡大した場合、拡大後の画像を構築するには元の画像の４倍の情報量が必要である。しかしこの拡大後画像を構築するための材料は元のちっこい画像しかない。そういう時に補間が必要になる。

例えば観測値から規則性を見出す場合も補間が使われるであろう。昨日の昼間の気温と明日の昼間の気温が分かっていれば、今日の昼間の気温を求めるに大概の人は足して２で割る。昨日と今日の気温が分かれば明日の気温も予測できる。データが増え、求めたい日時を自由に選択したければ観測された値のスキマを関数で補完することになる。

例えば少ないポリゴンから、ポリポリしないグラフィックを生成するには補間を用いたシェーディングが利用される。この場合はポリゴンの頂点に色情報がヒモ付られており、頂点が作る線なり面なりの色は補間によって決定される。多分。

こんな塩梅であるので、統計、ＡＩ、有限要素法、曲線描画、いろんなところで補完は顔を出す。