基礎から方向導関数について理解してみよう
この記事では『方向導関数』について、できる限り基礎からわかりやすく解説していこうと思う。
しかし、ここでは韓国の文理系共通高校数学のラスボス(!)、『数学Ⅱ』まで履修済みであることを前提とする。
つまり、下記の項目たちは前提知識として扱う。
・数列、数列の和 $${\sum}$$
・(主に多項式に関する)方程式/関数
・簡単な関数(連続関数、有利関数など)の極限
・三角関数の性質
・多項関数の微分法/積分法
ということでやっていこう。
まずは先ほどの前提知識を踏まえたうえでもっと必要そうな知識を見ていこう。
1. ベクトル
1.1. ベクトルの定義
……うん? ベクトル? となるかもしれないが、ちゃんと関連している。
まずベクトルは(略: Vec.)、平たく言うと『数の集まり』を縦にまとめたやつ。
このまとまった数のことを成分という。
ベクトル$${\begin{pmatrix}1\\2\end{pmatrix}}$$の成分は$${1}$$と$${2}$$で、$${\begin{pmatrix}-2\\0\\7\end{pmatrix}}$$のは$${-2}$$と$${0}$$と$${7}$$。
また、そのベクトルが持つ成分の個数を次元という。
記号として表すときはボールドの小文字か上に矢印をつけて表す。
英語の頭文字のvをよく使うんだけど、$${\mathbf{v}}$$か$${\vec{v}}$$になる。
$${\mathbf{v}}$$の次元は$${\dim(\mathbf{v})}$$って表したり。
あと縦で表すのがダメそうだったら$${\langle1,\;2\rangle}$$と書くのもあり。
小括弧で書いても大丈夫っちゃ大丈夫なんだけど、
座標と混同するかもだからここでは三角括弧で書かせてもらう。
さて、座標と混同するとは言ったけど、
成分が2個なら実質平面座標みたいなもんにならない?
ということで、成分が2個のときにゃ座標平面で表すことができる。
何で表すかと言うと、先ほどベクトル表記でも見かけた矢印で。
$${\begin{pmatrix}p\\q\end{pmatrix}}$$は横に$${p}$$だけ、縦に$${q}$$だけ伸びた矢印、って感じで表す。

普通矢印の始点は原点の$${(0,\;0)}$$が基本だけど、
どこからスタートしても方向&長さが同じなら同じベクトルになる。
$${(0,\;0)}$$から$${(4,\;3)}$$に伸びたベクトルと$${(2,\;4)}$$から$${(6,\;7)}$$に伸びたベクトルは
同じということ。どっちとも$${\begin{pmatrix}4\\3\end{pmatrix}}$$だし。

そして、ベクトルの次元が3に伸びたら座標平面ではなく座標『空間』に表す。
2次元が平面で、3次元が立体というのはどこかしらで聞いたことあるはず。
$${x}$$軸の右・左、$${y}$$軸の前・後ろに加えて$${z}$$軸の上・下でできた空間だよ。
$${\begin{pmatrix}p\\q\\r\end{pmatrix}}$$は横に$${p}$$、縦に$${q}$$、上に$${r}$$の分だけ伸びたベクトル。
例えば三次元ベクトル$${\mathbf{a}=\begin{pmatrix}2\\5\\5\end{pmatrix}}$$を座標空間に表したらこうなる。
このベクトルの始点は$${(0,\;0,\;0)}$$、終点は$${(2,\;5,\;5)}$$。

4次元以上のベクトルは、まぁ……座標超空間で表すこともできないわけではないんだけど、もう既に我々の次元(3次元)を超えてるんだから矢印には表さないようにしてる。ややこしいし。
『集まり』を言っているベクトルに比べて、ただの数字一個だけは『スカラー』と呼ぶ。$${3}$$はスカラーで$${\begin{pmatrix}3\\3\end{pmatrix}}$$はベクトルなんだね。
次元が1のベクトル、$${(3)}$$とかはまぁ一応ベクトルではあるけどスカラー扱い。
1.2. ベクトルの表現
線分のように始点と終点の名前と上矢印を使ってベクトルを表すこともできる。
先程例として挙げていたベクトルを引っ張ってくると、
①でのベクトル$${\mathbf{v}=\overrightarrow{\text{OA}}}$$、$${\mathbf{w}=\overrightarrow{\text{OB}}}$$、
②でのベクトル$${\mathbf{c}=\overrightarrow{\text{OP}}=\overrightarrow{\text{QR}}}$$、③でのベクトル$${\mathbf{a}=\overrightarrow{\text{OC}}}$$。
また、ベクトルは矢印の長さと向きさえ同じならば同じベクトルと言ったが、
逆を言うと長さと向きだけ言っちゃえばそのベクトルを説明できる。
矢印の長さ、つまりベクトルの大きさを「ノルム」と言い、
記号はここでは二重絶対値記号($${\lVert\mathbf{v}\rVert}$$)を使う。
普通の絶対値記号($${\lvert\mathbf{v}\rvert}$$)も使うんだが、本物の絶対値と混同しそうで。
求め方は簡単で、$${n}$$平方の定理の式の左辺に成分、右側にノルムを入れるだけ。
つまり$${\mathbf{v}=\begin{pmatrix}v_1\\v_2\\\vdots\\v_n\end{pmatrix}}$$のノルム$${\displaystyle\lVert\mathbf{v}\rVert}$$に対して$${v_1^{\;2}+v_2^{\;2}+\cdots+v_n^{\;2}=\lVert\mathbf{v}\rVert^2}$$、
まとめると$${\displaystyle\lVert\mathbf{v}\rVert=\sqrt{v_1^{\;2}+v_2^{\;2}+\cdots+v_n^{\;2}}=\sqrt{\,\sum_{k=1}^nv_k^{\;2}\,}}$$。
そして向きは、2次元限定にはなるのだが普通に角度として表す。
三角関数で半直線の角度を$${x}$$軸との反時計回りの角度で表したものと同様、
ベクトル$${\begin{pmatrix}c\\0\end{pmatrix}}$$($${c}$$は0ではない定数)との角度で表す。三角関数使ったら楽そう。

このベクトル$${\mathbf{v}=\begin{pmatrix}2\\5\end{pmatrix}}$$の
・ノルム$${\lVert\mathbf{v}\rVert=\sqrt{2^2+5^2}=\sqrt{29}}$$
・向きの余弦$${\displaystyle\cos\theta=\frac2{\,\sqrt{29}\,}}$$
ちなみにどうしても向きを$${\theta}$$単体で表したいんだったら三角関数の逆関数を使ってしまおう。$${\displaystyle\cos\theta=\frac2{\,\sqrt{29}\,}}$$なら$${\displaystyle\theta=\cos^{-1}\frac2{\,\sqrt{29}\,}}$$。
$${\cos}$$は$${0}$$以上$${\pi}$$以下なら逆関数になっても大丈夫だ!
(詳しい説明は【基礎微積分学:大学数学】のⅣを参考。)
そしてノルムが$${1}$$であるベクトルを「単位ベクトル(unit vector)」と言い、
記号ではよく$${\mathbf{u}}$$と表したりする。
1.3. ベクトルの基本演算
さて、このベクトルでも足し算とかは一部だけだけどできるようになっている。
まず数字だけで見てみよう。
・ベクトルの和/差:$${\begin{pmatrix}v_1\\v_2\\\vdots\\v_n\end{pmatrix}\pm\begin{pmatrix}w_1\\w_2\\\vdots\\w_n\end{pmatrix}=\begin{pmatrix}v_1\pm w_1\\v_2\pm w_2\\\vdots\\v_n\pm w_n\end{pmatrix}}$$(複号同順)
ex) $${\begin{pmatrix}2\\3\end{pmatrix}-\begin{pmatrix}5\\-1\end{pmatrix}=\begin{pmatrix}-3\\4\end{pmatrix}}$$
(足し算&引き算が成立するには両側の次元が同じである必要がある。)
・ベクトルのスカラー倍:$${c\begin{pmatrix}v_1\\v_2\\\vdots\\v_n\end{pmatrix}=\begin{pmatrix}cv_1\\cv_2\\\vdots\\cv_n\end{pmatrix}}$$
ex) $${-3\begin{pmatrix}2\\-4\end{pmatrix}=\begin{pmatrix}-6\\8\end{pmatrix}}$$
これまではまぁ、なんとかいけそう。
対応する部分同士で足したり、分配するだけだしね。
これを2次元ベクトルに限定して矢印で表すとどうなるか。
まずは足し算。
こういう風に一つ目の終点に二つ目の始点を合わせて、最終的な終点を調べる、みたいな感じ。

スタディサプリの堺先生の説明がわかりやすいと思ったので引用しよう。
(二つの2次元ベクトル$${\overrightarrow{\text{AB}}}$$と$${\overrightarrow{\text{BC}}}$$の和)
P「まずどこに行った?」
Q「$${\mathbf{A}}$$くんちから$${\mathbf{B}}$$くんちまで行った」
P「そっからどこに行った?」
Q「$${\mathbf{B}}$$くんちから$${\mathbf{C}}$$くんちまで行った」
P「結局あんたどっからどこまで行ったのよ?!」
Q「えー、$${\mathbf{A}}$$くんちから$${\mathbf{C}}$$くんちまで行った」
ということで$${\overrightarrow{\text{AB}}+\overrightarrow{\text{BC}}=\overrightarrow{\text{AC}}}$$。
『高1・高2 トップレベル数学ⅠAⅡB - 第22講. 分点公式と平面ベクトル』より
ベクトルが繋がっていなくても(AB-BCとかじゃなくてAB-CDとかになっている場合)、向き&大きささえ同じならそのベクトルは同じ、というのを使って動かしてしまえばいい。というか図で説明した$${\mathbf{v}+\mathbf{w}}$$がそうだしね。
そして、$${-\,1}$$をベクトルにかけるとそのベクトルの矢印は180°回転する。
逆側にくるん、と本当に綺麗に回転する。
ちょっと賢そうに言うと、$${\mathbf{v}}$$の始点に対して対称させたベクトルが$${-\,\mathbf{v}}$$。

また、正のスカラーをかけるとその分だけ長さが伸びる。
ノルムもそのまま伸びるよ。$${\lVert k\mathbf{v}\rVert=\lvert k\rvert\cdot\lVert\mathbf{v}\rVert}$$。
ノルムは常に$${0}$$以上だから絶対値は基本。

1.4. ベクトルのドット積
さて、足し算&引き算をやったのなら次は掛け算だろう。
ベクトルの掛け算はなぜか死ぬほど種類がある。
そのうち今回扱うのは$${\mathbf{v}\cdot\mathbf{w}}$$と表せる内積。
……というと少し間違った説明になって、
実際は「ドット積(Dot product)」を扱う。
「ベクトルの内積(Inner pdct.)」の中には色々種類があって、
その中に私たちの今回扱う「ドット積」がある、という感じだ。
別名「スカラー積(Scalar pdct.)」。先ほどのスカラー倍とは違うよ。
二つのベクトル$${\mathbf{v}=\begin{pmatrix}v_1\\v_2\\\vdots\\v_n\end{pmatrix}}$$と$${\mathbf{w}=\begin{pmatrix}w_1\\w_2\\\vdots\\w_n\end{pmatrix}}$$のドット積
$${\mathbf{v}\cdot\mathbf{w}=v_1w_1+v_2w_2+\cdots+v_nw_n=\displaystyle\sum_{k=1}^n v_kw_k}$$と定義される。
つまり、対応される成分同士をかけて足せばいいってことだね。
$${\begin{pmatrix}2\\3\\7\end{pmatrix}\cdot\begin{pmatrix}1\\0\\-\,0.5\end{pmatrix}=2\cdot1+3\cdot0+7\cdot(-\,0.5)=-\,1.5}$$ということ。
これも足し算同様、二つのベクトルは次元が同じである必要があるよ。
また、ドット積では交換法則が成立する。
つまり$${\mathbf{v}\cdot\mathbf{w}}$$であろうが$${\mathbf{w}\cdot\mathbf{v}}$$であろうが同じ。
$${\displaystyle\sum_{k=1}^n v_kw_k}$$も$${\displaystyle\sum_{k=1}^n w_kv_k}$$も同じだしね。
……さて、このドット積の出力値、ベクトルではないよな。
なぜかベクトルとベクトルをかけたのにスカラーが出てきやがる。
だから「スカラー積」という別名がついたらしい。
そして、スカラー同士での計算では中点($${\cdot}$$)もバツ記号($${\times}$$)も、
同じようなものだけど、ベクトルでは$${\cdot}$$と$${\times}$$は違う。
$${\mathbf{v}\times\mathbf{w}}$$を$${\mathbf{v}\cdot\mathbf{w}}$$と同じ方法で計算はできない。
くれぐれもドット積を$${\mathbf{v}\times\mathbf{w}}$$のように表記しないように。
1.4.2. ドット積のまた違う定義
さて、ドット積の結果はまた違う形として表現できる。
どの次元のベクトルであれ、二つのベクトル$${\mathbf{v}}$$、$${\mathbf{w}}$$を矢印で表すと
その矢印を一つの平面の上にあるように調整することができる。
位置によって左右されないベクトルの特権とも言おうか。
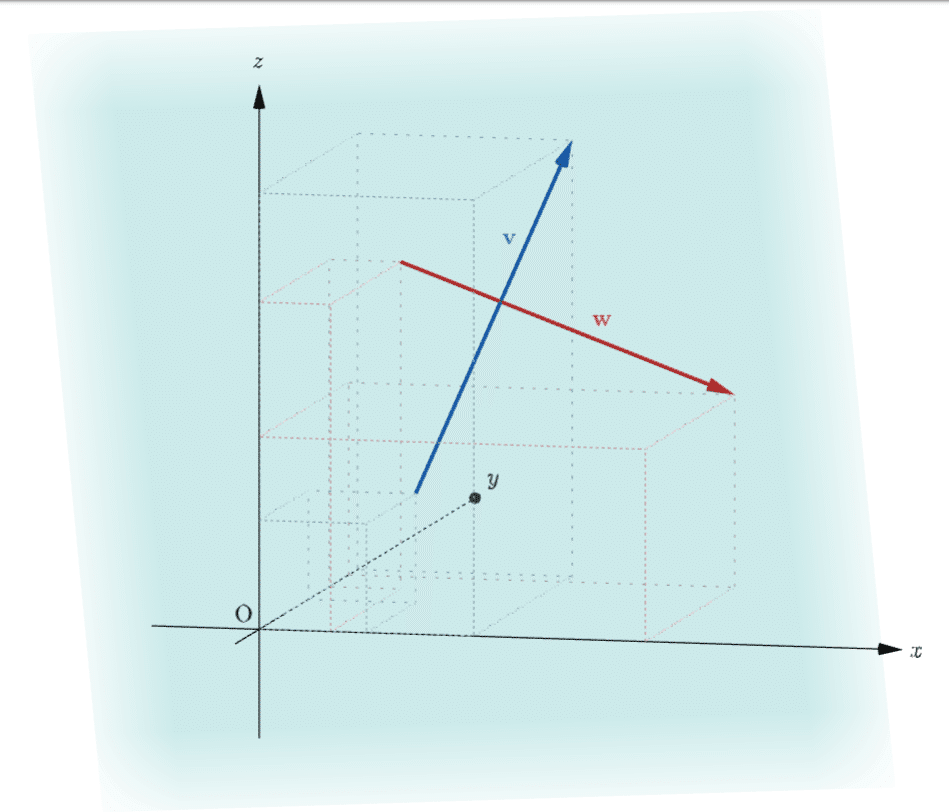
その平面の中で始点が同じになるように調整すると、
一つの角が出てくる。その角を$${\theta}$$とする。

この二つのベクトルと角$${\theta}$$を使って、
ベクトルのドット積を先程とは違う方式で定義することができる。
ベクトル$${\mathbf{v}}$$、$${\mathbf{w}}$$が成す角の大きさが$${\theta}$$であるとき、
$${\mathbf{v}\cdot\mathbf{w}=\lVert\mathbf{v}\rVert\lVert\mathbf{w}\rVert\cos\theta}$$と定義される。
これをドット積の「幾何的定義」という。
角という非常に幾何的なものをつかっているから。
最初に紹介した定義は「代数的定義」という。数学だけで定義したから。
2. 多変数関数と偏微分
2.1. 多変数関数
高校まで学んだ関数は$${f(x)}$$という変数が$${x}$$一つしかない「一変数関数」だ。
「$${y=f(x)}$$だから2つじゃん!」という主張は間違い。
$${y}$$は出力値。ここでの変数は入力値なので$${x}$$の一つしかない。
ここで、ちょっと脱線して、記号を少し見てみよう。
「○○数全ての集合」を表すときには、その数の種類を代表できるアルファベット一文字を二重に書く(黒板体と呼ぶ。)で書いた記号を使う。
実数はReal numberから$${\mathbb{R}}$$、
自然数はNatural no.から$${\mathbb{N}}$$、
整数はZahlenから$${\mathbb{Z}}$$、(ドイツ語)
有理数はQuozienteから$${\mathbb{Q}}$$。(イタリア語で「商」)
残りはあんまり使わないので今回はパス。
これをなんで今言及したかというと、先ほどの一変数関数をこれを使って表すことができるためである。
実数の入力値から実数の出力値が出るため、
$${f(x)}$$を$${f\!:\;\mathbb{R}\longrightarrow\mathbb{R}}$$と表すことができる。
さて、ここからが面白いところだ。
入力する空欄が一つ増えたらどうなるんだろう? という考えに答えたのが
「二変数関数」という概念だ。文字通り変数が二つになった関数。
このときの変数は一般的に$${x}$$と$${y}$$を持ってくる。出力のほうには$${z}$$を。
二変数関数も先ほどの$${\mathbb{R}}$$を使った表記ができるのだけれど、
このとき入力値に実数を二つ使った、という表現をしたい。
横暴論ではあるが$${\mathbb{R}\mathbb{R}=\mathbb{R}^2}$$なので、
二変数関数$${g(x,\;y)}$$を$${g\!:\;\mathbb{R}^2\longrightarrow\mathbb{R}}$$と表してしまおう。
これで「二つの実数の入力して一つの実数が出力される」、ということになる。
この二変数関数は軸が3つもいる($${x}$$入力、$${y}$$入力、$${z}$$出力)ので、
もはや紙の上には表すこともできなくなってしまった。
ということで次元を増やそう。2次元から3次元に行こう!!
……で、誕生したのが先ほどの座標平面ってわけだ。
ここに$${x}$$と$${y}$$に関する式をぶち込んどけば3次元のグラフができあがり。
試しに$${x^2+y^2}$$を入れると筆の先っぽみたいな形のグラフが出てくる。

まぁこういうのもあるんだな~って認識で大丈夫。
別にこの形を覚えて何かをする、ってわけではないから。
2.2. 偏微分
さて、(韓国の)『数学Ⅱ』で「多項関数の微分法」たるものは学んだ。
$${\displaystyle\frac d{\,dx\,}x^n=nx^{n-1}\;\;(n\in\mathbb{N})}$$というやつ。
一応軽く振り返っておくと、
$${\displaystyle\frac d{\,dx\,}f(x)=\frac{df}{\,dx\,}}$$というのは$${f(x)}$$を$${x}$$に対して微分しろ、という記号。
もし微分する文字が明確な場合$${f'}$$や$${f'(x)}$$などと表記しても問題なし。
定義としては$${\displaystyle\frac {df}{\,dx\,}=\lim_{\mathit{\Delta} x\to0}\frac{\mathit{\Delta}f}{\,\mathit{\Delta}x\,}=\lim_{\epsilon\to0}\frac{f(x+\epsilon)-f(x)}\epsilon}$$という感じ。
それで、微分が一体なんなのか、というのはざっくり言うと、
微分係数と呼ばれる$${\displaystyle f'(a)=\left.\frac {df}{\,dx\,}\right|_{x=a}}$$は
① $${x=a}$$のときのままの勢いでの$${f}$$の変化量
② $${y=f(x)}$$のグラフの上の点$${(a,\;f(a))}$$で引いた接線の傾き
と説明することができる。
ちなみに$${\left.P(x)\right|_{x=a}=P(a)}$$ね。
この$${a}$$を元々の$${f(x)}$$の定義域まで広げた$${f'(x)}$$が導関数。
この導関数を求める過程を微分、もしくは微分法というよ。
さて、本題に戻ろう。今回やりたいのは、多変数関数の微分。
……どうやるの? という感じだが、割と簡単。
先程$${\displaystyle\frac{df}{\,dx\,}}$$が$${f}$$を$${x}$$に対して微分する、と言うことだと言ったが、
元関数の変数が増えたと言って大してこの理屈は変わらない。
ただ、「変数がたくさんあるがこれしか扱わない」という意思を見せるため、
$${d}$$の代わりに$${\partial}$$を使う。$${6}$$を逆にしたみたいな形。
「デル(del)」とか「ラウンド(round)」とかいうよ。YKはdel派。
ということで、多変数関数$${f(x_1,\;x_2,\;\cdots,\;x_n)}$$に対して
$${\displaystyle\frac{\partial f}{\,\partial x_i\,}}$$は$${x_i}$$のみを変数と見なした微分、$${x_i}$$に対しての偏微分という。
また、偏微分の結果を偏導関数というよ。
$${\displaystyle\frac{\partial f}{\,\partial x_i\,}}$$の代わりに$${f_{x_i}}$$という表記でも偏微分を表すことができる。
番号がついてるもの限定で$${f_i}$$という表記も可能。
偏微分の例を少し挙げておこう。「なんのこと??」ってなるかもだし。
偏微分対象の変数が含まれない項は普通に定数項扱いだから微分したら$${0}$$だよ。
三変数関数$${g(x,\;y,\;z)=3x^2z+4y^3z}$$に対して
$${\displaystyle g_x=\frac{\partial g}{\,\partial x\,}=6xz}$$
$${\displaystyle g_y=\frac{\partial g}{\,\partial y\,}=12y^2z}$$
$${\displaystyle g_z=\frac{\partial g}{\,\partial z\,}=3x^2+4y^3}$$
2.3. 多変数関数の勾配(Gradient)
勾配……ってなんぞや? と思うかもしれないが、こちらも割と簡単。
軽~く言ってしまうと、全ての変数に対しての偏導関数を成分とするベクトル。
関数$${f(x_1,\;x_2,\;\cdots,\;x_n)}$$に対して$${f}$$の勾配$${\mathbf{\nabla}f=\begin{pmatrix}f_1\\ f_2\\\vdots\\f_n\end{pmatrix}}$$ということ。
$${\mathbf{\nabla}}$$ ← この記号は「ナブラ(nabla)」か「デル(del)」と言う。YKはNabla派。
よく見ると太字にしてあるのがポイント。ベクトルだからね。
手書きなら二重重ねでもよさそう。パソコンじゃできないけど。
先程の$${g(x,\;y,\;z)=3x^2z+4y^3z}$$を持ってくると
$${\mathbf{\nabla}g=\begin{pmatrix}6xz\\12y^2z\\3x^2+4x^3\end{pmatrix}}$$。
これを何に使うかは~……。まだ内緒。
3. 方向導関数(Directional derivative)
さて、ようやく本題にたどり着けた。
方向導関数とはなんぞや。方向のある導関数? ん?
3.1. 方向導関数の定義
今回求める方向導関数の元関数は二変数関数。
座標空間に表したいので関数を$${z=f(x,\;y)}$$としましょう。
さて、導関数はその点での出力値(今回は$${z}$$)の変化量を調べた結果。
なんだが、3次元グラフでは変化量をどう求めればいいのかわからない。
$${x}$$軸方向? $${y}$$軸方向? それとも$${y=x}$$直線の方向?
どんな方向でも一応変化量は求めることができるんですよ。
ということで、方向を全ての方向にできるようにしてしまおう。
「~の方向への方向導関数」を設定するようにするのだ。
その方向をどうやって設定するのか。……ベクトルがあるじゃないか!!
ベクトルは向きと大きさで決まるからそれを利用すればできそう。
そして別に$${z}$$方向には進まなくてもいいし、$${y}$$方向も使わないと困るし、という感じでベクトルの次元は$${2}$$。
でも大きさは別にいらない。どうせ「変化量」だからあとで割るんだしさ。
ということで使うのは単位ベクトル。大きさが$${1}$$になるように調整しよう。
もし提示された方向が単位ベクトルじゃなかったら、適当な正のスカラーをかけて単位ベクトルにさせてしまおう。
$${\begin{pmatrix}a\\b\end{pmatrix}}$$なら$${\displaystyle\frac{1}{\,\sqrt{a^2+b^2}\,}}$$をかけて$${\begin{pmatrix}\displaystyle\frac{a}{\,\sqrt{a^2+b^2}\,}\\\displaystyle\frac{b}{\,\sqrt{a^2+b^2}\,}\end{pmatrix}}$$にしちゃえばOK。
そして変化量って言ってるくらいだし、
$${f}$$の偏微分を集めた勾配$${\mathbf{\nabla}f(x,\;y)=\begin{pmatrix}f_x\\f_y\end{pmatrix}}$$を求めちゃって、
これで方向導関数を求める準備は全て終わった。
単位ベクトル$${\mathbf{u}}$$方向への方向導関数$${D_{\mathbf{u}}f(x,\;y)=\mathbf{\nabla}f(x,\;y)\cdot\mathbf{u}}$$
こちらが定義。割と式は簡単だなぁ、というのが初印象でした。
3.2. 方向導関数の意味
先程「方向を指定した$${z}$$の変化量」と言ったが、実際なんなのか。
この画像を見ながら話していこうと思う。

まず$${z=f(x,\;y)}$$のグラフの上の点$${(a,\;b,\;f(a,\;b))}$$を始点とした$${\mathbf u}$$を描いて、
その方向に対しての接線を引いてみる。上の画像なら緑色の線だね。
ちなみに線の通ってる四角いやつは接平面。文字通り点に接している平面だよ。
$${\mathbf u}$$で方向を指定しないまま微分したらこうなる。
$${\mathbf u}$$の大きさが$${1}$$なのを利用して、$${\mathbf u}$$の終点から接線と交わるまで$${z}$$軸方向に伸びたベクトル($${\mathbf h}$$)の大きさをその接線の変化量と言えるだろう。
ということで$${D_{\mathbf u}f(a,\;b)=\lVert\mathbf h\rVert}$$。一般的になるように言い直すと
$${D_{\mathbf u}f(x,\,y)}$$は点$${(x,\;y)}$$で$${\mathbf u}$$の方向に引いた接線の$${z}$$の変化量を意味する。
3.3. 方向導関数の練習
Q. 曲面$${z=\displaystyle\frac{\,1\,}2xy}$$の$${\mathbf{v}=\begin{pmatrix}3\\4\end{pmatrix}}$$方向への方向導関数を求め、
また$${z}$$の上の点$${(2,\;3,\;3)}$$での$${\mathbf v}$$方向への$${z}$$の変化量$${\mathit{\Delta} z_\mathbf{v}}$$を求めなさい。
まず $${\mathbf{\nabla}z=\begin{pmatrix}0.5y\\0.5x\end{pmatrix}}$$(縦幅が広くなるので分数の使用は避けた。)、
そして$${\mathbf{v}}$$は単位ベクトルではないので、平方数を使って単位ベクトルに直すと$${\displaystyle\mathbf{u}=0.2\mathbf{v}=\begin{pmatrix}0.6\\0.8\end{pmatrix}}$$となる。
$${\mathbf{v}}$$方向への方向導関数を求めると
$${D_{\mathbf u}z(x,\;y)=\mathbf{\nabla}z\cdot\mathbf{u}=0.5\cdot0.6y+0.8\cdot0.5x=0.4x+0.3y}$$
またこの$${(x,\;y)}$$に$${(2,\;3)}$$を代入した$${D_{\mathbf u}z(2,\;3)}$$は問題の$${\mathit{\Delta}_{\mathbf v}z}$$と同じなので$${\mathit{\Delta}_{\mathbf v}z=D_{\mathbf u}z(2,\;3)=0.8+0.9=1.7}$$
$${\therefore\;D_{\mathbf u}z(x,\;y)=0.4x+0.3y}$$, $${\mathit{\Delta}_{\mathbf v}z=1.7}$$
いかがだっただろうか。
まぁ日常で使う場合はほとんどはないと思うが、「へぇ~、こんなもんもあるんだ」「3次元での変化量はこうやって求めるんだ」と思っていただけたなら幸い。
間違いやご意見などあるのならコメントに。
では、また次の記事で。
この記事が気に入ったらサポートをしてみませんか?
