システムトレーダーのためのデータ分析
バックテストでわかるのは、バックテストを行った結果だけであって、そのトレードシステムが将来、「どの程度の利益を見込めるのか」、「いいときと悪いときの振れ幅がどれくらいか」といった未知の数字の推定はできません。

リアルトレードでのEAのドローダウンは「偶然によるものか」、「システムを停止するべき異常事態か」、これを判断しなければいけない状況が必ず訪れます。
この判断を
● 主観でしてしまうのか、
● データ分析によって判断基準を設けておくのか、
どちらが良いかを考えるとデータ分析の必要性は明確だと思います。この記事ではトレードでよく使われるデータ分析をいくつか解説します。
◆モンテカルロ分析
モンテカルロ分析はトレードの結果のように不確実なものの将来起こりうる結果を推定するために使われる数学的な技法です。正確な推定ができるためトレード以外でも販売予測、株価、天気予報などさまざまなところで活用されています。
モンテカルロ分析の手順
EAのバックテストによって得た損益データを用意する
損益データから1トレード、ランダム抽出する
ランダム抽出を何度も繰り返し、新たな損益データを作る
新たな損益データを数百、数千個作成する

ランダムサンプリングによって作られた新たな損益データをわかりやすく言うと「こんな結果もあり得たよね」というデータです。ランダムサンプリングで集められた損益データのため元のデータより良い結果である可能性も悪い可能性もあります。
ランダムサンプリングで集められた損益データの平均値は統計学の中央極限定理により必ず正規分布となります。
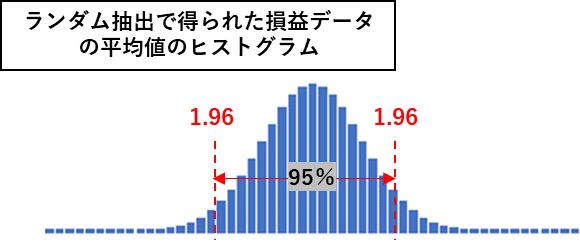
分析対象のシステムが独立試行であると仮定するなら、ランダム抽出された損益データ数百、数千個から、その平均値や標準偏差を計算することで「どれくらい数値がばらついているのか」という情報が得られ、それがそのまま将来のシミュレーションとなります。
実際に分析した例
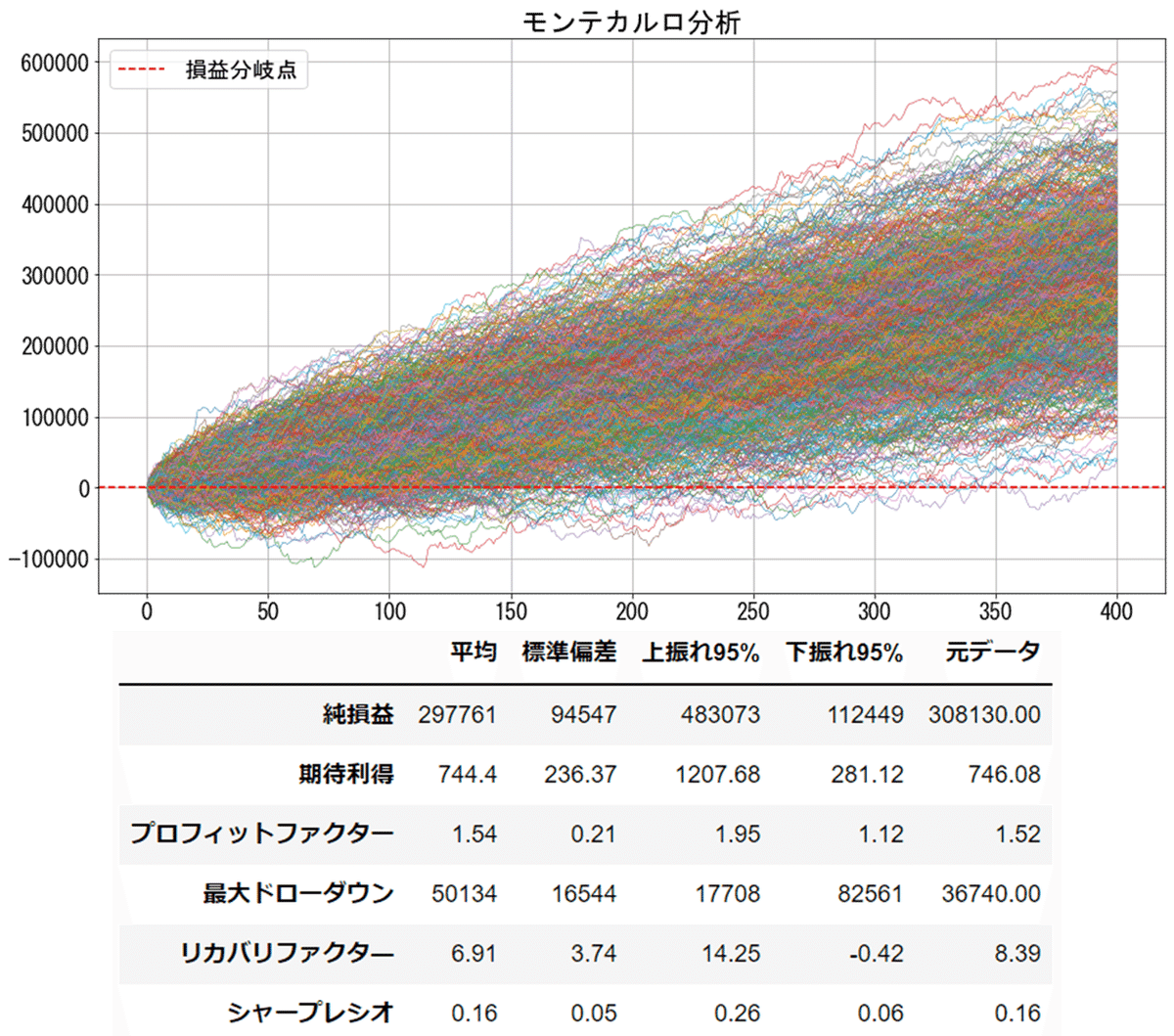
これが実際にモンテカルロ分析を行った結果です。各400トレード分をランダムサンプリングして集めた損益データを1000サンプル作成しています。
ここで結果の表に注目します。

①はモンテカルロ分析で集めた1000サンプルの平均値です。元のデータとおよそ同じ数値に近づきます。
②は1000サンプルの標準偏差です。この数値は低いほうがバラツキが少なく安定していることを示します。
③は各項目の上振れ値です。(平均 + 1.96 * 標準偏差)
④は各項目の下振れ値です。(平均 - 1.96 * 標準偏差)
このEAを運用して約400トレード行うと約95%の確率で③と④の間に結果が収まることが推定されます。たとえ元データの期待値がプラスのEAであっても④の下振れ値がプラスになるとは限りません。
実運用するときには③と④の間で結果がぶれることを想定する必要があるため、④の下振れ値くらいの結果は今後も起こる可能性があると考え、この数値が許容できるEAのみを実運用するようにしましょう。
モンテカルロ分析の欠点
モンテカルロ分析は独立試行のシステムの振れ幅を推定、シミュレーションする場合においては、高い精度で分析することが可能ですが
システムが強い従属試行である場合や
複数ポジションを持つシステム
このような損益データがランダムサンプリングによって並び変わってしまう分析方法が適さないシステムの評価には向かないです。損益データの並び替えをしない分析手段を次に解説します。
◆スタートトレード分析(ムービングスタート分析)
スタートトレード分析は移動平均の要領でひとつのバックテストの損益データから抽出期間をシフトしながら計算を行います。ムービングスタート分析とも呼びます。
スタートトレード分析の手順
100トレード分のスタートトレード分析を行うとするとその手順は
EAのバックテストによって得た損益データを用意する
1トレード目から100トレード目までを抽出し新たな損益データを作る
2トレード目から101トレード目までを抽出し新たな損益データを作る
3トレード目から102トレード目までを抽出し新たな損益データを作る
これを最後まで繰り返し行う

このようにモンテカルロ分析とは別の手段で複数の損益データのサンプルを集めることができます。スタートトレード分析によって得られたデータは時間とともにEAのパフォーマンスがどのように変化しているのかがわかります。「いつも安定して利益を上げているものなのか」、「時期によって結果にバラツキがある不安定なものなのか」というような情報を調べることができます。
実際に分析した例

スタートトレード分析では各評価指標(期待利得やプロフィットファクターなど)の推移の様子をグラフにすることができます。この例では期待利得、プロフィットファクター、シャープレシオ、最大ドローダウン、リカバリファクタ―の5種類の評価指標を算出しているので結果のグラフは5つ存在します。
期待利得のグラフをピックアップして時間とともにEAのパフォーマンスがどう変化したかを確認してみましょう。

このEAの例では前半では期待利得500未満を推移していましたが、後半は期待利得が常に1000を超えていることがわかります。

①はスタートトレード分析の全結果の平均値です。
②は各評価指標の最低の結果です。
③は各評価指標の最高の結果です。
④はスタートトレード分析の全結果の標準偏差です。
将来の結果がテストの延長であると仮定するなら、この先の実運用の結果は②の最小から③の最大の範囲に収まる可能性が高いと考えられます。
モンテカルロ分析のときと同様に、たとえ元データの期待値がプラスのEAであっても②の最低値がプラスになるとは限りません。
実運用するときには②と③の間で結果がぶれることを想定する必要があるため、②の最低値くらいの結果は今後も起こる可能性があると考え、この数値が許容できるEAのみを実運用するようにしましょう。
◆従属試行テスト
モンテカルロ分析はEAが独立試行であるときに適しており、従属試行である場合やナンピン等の複数ポジションの場合はスタートトレード分析が適していると解説しました。
次は、分析するEAが従属試行なのか独立試行なのかわからないときはどのように調べるといいかを紹介します。
従属試行のトレード戦略とは
独立試行とは、個々のトレードが独立している傾向があることをいい、例えば「勝率60%なのに5連敗しているから、次は勝つ確率が高いだろう」とはならず、どんなタイミングであっても次の1トレードで勝つ確率は一定です。
従属試行とは、次の1トレードで勝つ確率は一定とはならない傾向があることをいいます。勝ちや負けが続きやすい傾向(正の従属性)や反対に、勝ちや負けが交互に起こりやすい傾向(負の従属性)があるEAが従属試行であるといえます。

EAが従属試行であるかどうかを調べる方法はたくさんあると思いますが、今回はランテストと自己相関を使ったやり方を紹介します。
ランテスト(Zスコア)

この計算式でZスコアを求めます。EAの勝率が50%で完全な独立試行であればZスコアは95%の確率で 1.96 ~ -1.96 の範囲に収まります。つまり、この範囲に収まらないEAは従属試行である可能性が高いと考えられます。

より高い精度で分析するために、このZスコアをスタートトレード分析によって時間とともにどのように推移しているかをチェックします。
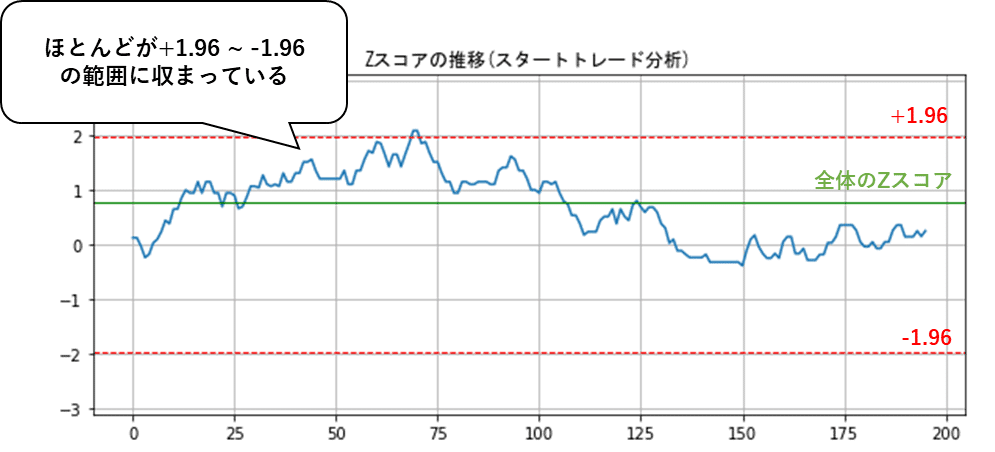
このスタートトレード分析の結果ではほとんどの期間が +1.96 ~ -1.96 の範囲に収まっていて、全体のZスコアも範囲内なので独立試行に近いと考えられます。
従属試行だと判断する条件の一例は
● 全体のZスコアが +1.96 ~ -1.96 の範囲外になっていること
● 分析期間の50%以上 +1.96 ~ -1.96 の範囲外になっていること
ランテストはトレード結果に正規性があるときに高い精度を示すものであるため、特に勝率が極端に高い、または低いEAに対しては信頼度の低い分析になってしまいます。これだけで従属試行かどうかを判断するのは良くないため、次に解説する自己相関と併せて分析する必要があると思います。
自己相関
トレード結果を一つ前のトレードと比較して、相関関係にあるかどうかを調べる分析方法です。もし正相関か負相関のどちらかがあればひとつ前のトレード結果次第で次のトレードの確率および期待期が変わるということなので、従属試行である可能性を示していると考えられるでしょう。

自己相関係数はどれくらい数値があれば従属試行だと判断できるのかについてラルフ・ビンスの著書の中で参考値が書かれているので一部引用させて頂きます。
先物トレーディングシステムの場合、高い相関係数とは0.25~0.30より大きい (正の場合) か、-0.25~-030より小さい (負の場合) 場合をいう。一般に、強い正の相関があるとき、大きな勝ちのあとに大きな負けが続く(あるいはその逆)ことはほとんどなく、強い負の相関 (相関係数が0.25~-0.30を下回る)があるとき、大きな負けのあとに大きな勝ちが続く(あるいはその逆) 傾向が強い。
先物トレーディングの場合とはありますがFXのシステム開発にも参考になる数値だと思います。少し私の経験からの主観をはさむと、自己相関係数が+0.25以上、-0.25以下になるEAは、偶然ではなかなか起こらないような強い従属試行だと思います。
自己相関も同様により高い精度で分析するために、スタートトレード分析によって時間とともにどのように推移しているかをチェックします。

このスタートトレード分析の結果ではほとんどの期間が +0.25 ~ -0.25 の範囲に収まっていて、全体の自己相関係数も範囲内なので独立試行に近いと考えられます。
従属試行だと判断する条件の一例は
●全体の自己相関係数が +0.25 ~ -0.25 の範囲外になっていること
●分析期間の50%以上 +0.25 ~ -0.25 の範囲外になっていること
◆線形回帰
回帰分析のざっくりとした説明
線形回帰分析(単回帰分析)を図で簡単に説明します。

この回帰直線(予測線)は最小二乗法によって求めることができます。
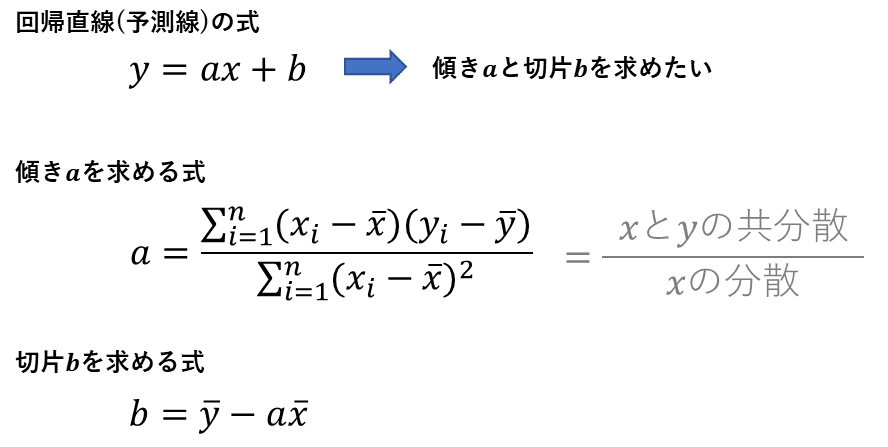
次に残差と決定係数について説明します。残差とは回帰直線(予測線)と各データの差の大きさで、残差が全体的に小さいと全体のバラツキが小さくなります。
決定係数とは回帰の適合度を測る数値で、データがどれくらい回帰直線の周りにまとまっているかによって決まります。つまり、全体的に残差が小さくまとまっているデータほど決定係数は大きくなります。

これをEAのバックテストデータに対して行い、EAの評価やリアルトレードの推定をしようというのが目的です。
実際に分析した例

傾きと切片は回帰直線を表す数値ですが、傾きに関しては「1トレードでだいたいどれくらいの利益が見込めるか」を示しています。
「1トレードでだいたいどれくらいの利益が見込めるか」といえば期待利得も同じような意味ですが、傾きは別のアプローチによって算出されたものです。傾きと期待利得はおおよそ同じような数値になりやすいです。
標準化残差は、残差がだいたいどれくらいの大きさかを示し「損益のバラツキの大きさ(リスク)がどれくらいか」を測るものです。最小残差はマイナス方向に最大でいくら大きくなったかです。最大ドローダウンと最小残差を比較すると最大ドローダウンは縦方向の落ち込みしか反映されないのに対して、最小残差は「長い横ばい期間」も反映するため、最大ドローダウンよりも価値ある情報となる可能性もあるかもしれません。
決定係数と相関(損益グラフと回帰直線の相関係数)はどちらも「損益グラフがどれくらい直線に近いか」を示す数値です。決定係数は損益グラフがまっすぐ安定した形であるほど1.0に近づき、バラツキが大きいほど0.0に近づきます。
最後の「傾き÷( 1 + 標準化残差 )」は、
● 1トレードでだいたいどれくらいの利益が見込めるか
● 損益のバラツキの大きさ(リスク)がどれくらいか
このどちらも反映した数値です。シャープレシオに似ていますがシャープレシオは損益が正規分布から遠いトレード戦略ほどネガティブな結果を示すという欠点があるのに対して、これは正規性を反映するものでないため、多くの種類のEAに対して公平に評価をすることができます。
精度の高いデータ分析を行うために…
高い精度でデータ分析を行うには、まず前提としてカーブフィッティングしていないバックテストデータが必要です。システム開発者の心理的には良い結果が出たバックテストを重要なものだと感じ、悪い結果は軽視してしまいます。バックテストの結果もリアルトレードと同様に振れ幅があるので、良い結果も偶然の上振れだった可能性もあるわけです。
●アルファリスク
「実力がないシステムを過大評価してしまうリスク」
●ベータリスク
「実力があるシステムを過小評価してしまうリスク」
バックテストがシステムの実力以上の結果であったとき、そのデータで詳細分析を行えば、本来取るべきリスクを低く見積もり(自信過剰)、いざリアルトレードを行えばなんともないドローダウンで停止条件に引っかかる「システムの損切り貧乏」になってしまいます。
アルファリスクやベータリスク避けるためのバックテストの知識やノウハウは過去のnote記事でも投稿しているのでよければ併せてチェックしてみてください。
この記事が気に入ったらサポートをしてみませんか?
