ミニ四駆と空力(その3)

「ダウンフォースだ！」
ミニ四駆と空力の記事、第3回です。
前回の記事で、ジャンプの飛距離が3枚着地となる速度のときに2枚着地に収めるのに必要なダウンフォースが0.36Gであることがわかりました。
今回は、ミニ四駆が0.36Gのダウンフォースを発生させることは可能なのかを考えていきます。

前回、前々回の記事はこちらです。

ダウンフォースとG

前回の記事ではダウンフォースをG(加速度)という形で表現していましたが、実はこれ、厳密に言うと正しい表現とは言えません。

ダウンフォースとは、車体やウイングが発生させる下向きの揚力、すなわち「力」であり、加速度ではありません。

ミニ四駆が路面を走っている場合は、落下速度はゼロです。なので、どんなにダウンフォースで下に押されようと、そもそも落下していないので、落下速度が増していくことはありません。つまり、車体が路面に押さえつけられはするものの、G(加速度)は生じないのです。ダウンフォースがあるからといって、いつでもGが生じるわけではない、ということです。

一方、ミニ四駆が空中に浮いているときは、ダウンフォースによって落下速度が加速していきます。つまり、ダウンフォースによってGが生じているということです。

Gは、ダウンフォースが大きいほど、そしてミニ四駆が軽いほど、大きくなります。なので、ミニ四駆の重さが異なると、ダウンフォースの強さが同じでも、Gの大きさは変わってきます。

ジャンプの飛距離を計算する上では、必要な数値は加速度です。力としてのダウンフォースを使って計算しようとすると、ミニ四駆の重さを仮定した上で、加速度をいちいち算出しなければなりません。
なので、計算に便利な加速度として、ダウンフォースによって生じるGを、便宜上「ダウンフォース」と表現していました。

あくまでもダウンフォースとは「力」であり、ダウンフォースという力を受けたことで「物体に生じた加速度」がGである、というのが厳密な表現です。

ただし、現実のレースカーの分野でも「1.8G」などというように、Gいう形でダウンフォースを表現するようです。これは、車体が地球から受けている重力の大きさに対する比率という形でダウンフォースを表現しているものと思われます。1.8Gといった場合は、車体重量の1.8倍の大きさのダウンフォースということです。
今回の検証で出てくる数値も同様の表現が可能で、今回求めようとしているダウンフォースは「0.36G」と表現でき、すなわち、車体重量の0.36倍の力となります。

以降、この記事では

ダウンフォース : 車体やウイングが発生させた力(揚力)
G : ダウンフォースにより生じた加速度、または、ダウンフォースの大きさを車体重量との比率で表した数値

という意味で用語を使っていきます。

ダウンフォース計算に必要な要素

前置きが長くなりましたが、ダウンフォース(揚力)を求める計算式は次のとおりです。

また、ダウンフォースとGには、次のような関係が成り立ちます。

この2つの関係式をまとめると、

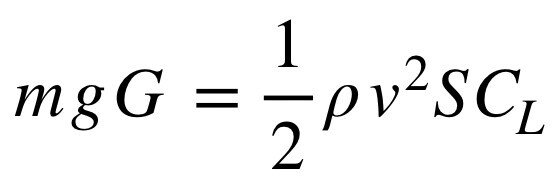
となります。
色んな要素が記号として出てきますが、
・質量mは、ひとまず私のミニ四駆の質量(電池込み150g)と仮定
・gは地球の重力加速度なので調べたらわかる(9.80665m/s^2)
・Gは前回の記事で求めた0.36G
・ρ(ロー)は地上の空気密度なので調べたらわかる(1.225㎏/㎥)
・速度vは、前回の記事で求めた3枚着地になる5.9m/s
ということで、現時点でわからないのは、代表面積Sと揚力係数CLの2つとなります。
これら2つをハッキリさせれば、検討を前に進めることができそうです。

ミニ四駆の「代表面積」とは

代表面積とは、自動車のダウンフォースを計算する場合、水平投影面積を用います。

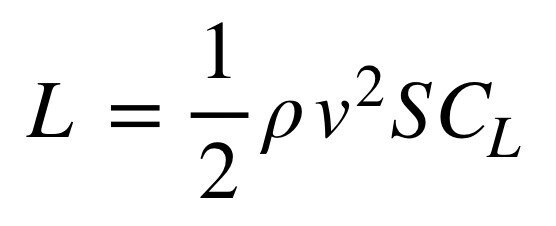
(ちなみに、この式は、飛行機の翼の揚力を計算するために使われる式で、飛行機の場合は翼面積が代表面積になります。)

水平投影面積は、単純に、車体の全幅×全長とします。
全幅は、左右のローラー径(13㎜と仮定)とスライドダンパーやピボットバンパーの可動域(片側4㎜と仮定)を、レギュ上の上限105㎜から差し引いて、71㎜とします。
全長は、レギュ上の上限である165㎜とします。

全幅71㎜と全高165㎜をかけ算し、代表面積は11715m㎡と求めることができます。これで代表面積Sはハッキリしました。

揚力係数CLについて

揚力係数とは、揚力を計算するのに使われる数値であり、車体がダウンフォースを発揮する能力の大きさと言い換えてもいいでしょう。

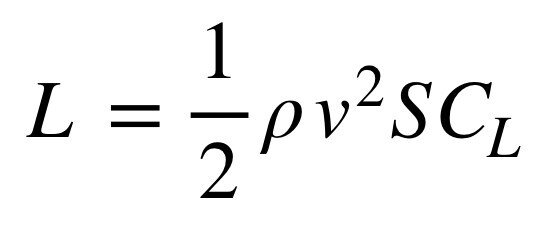
この式を見ると、右辺の諸々をかけ算したものが揚力と分かります。揚力係数もかけ算されますので、揚力係数が大きいほどダウンフォースも大きくなります。

この式の揚力Lをマシン質量とGで置き換えた式がこちらでした。

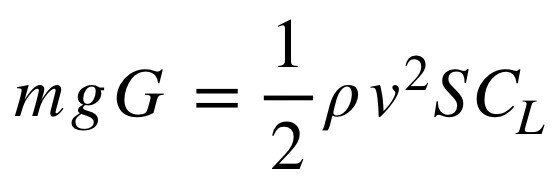
マシンの質量は150g(電池込み)とします。
これまでの道のりで、すでに揚力係数以外の数値は明らかになっています。
なので、この式を揚力係数CLについて解けば、0.36Gを発揮させるダウンフォースを得るのに必要な揚力係数の数値が分かります。

計算してみると、必要な揚力係数は約2.12となりました。

まとめ

今回の検討で、次の事項が明らかになりました。

・3枚着地の速度(5.9m/s)のまま、２枚着地に収めるのに必要なダウンフォースは0.36G(車体重量の0.36倍)で、
「そのために必要な揚力係数は2.12」

つまり、揚力係数2.12を達成できれば、必要なダウンフォースを得られるということです。
では、揚力係数2.12という値は、実現できるものなのでしょうか？
次回はこれについて考察していきます。

次回