「0で割る」ことができない理由と0で割れたらどうなるかの考察

小学校の算数でやる割り算、そして分数。割り算は0で割ってはいけない、そして分数も分母が0になってはいけないということも教えられたか、もしくは暗黙の了解でやらなかったと思います。今回は、0で割ってはいけない理由と、「もし0で割れたらどんな世界になるのか？」ということも紹介していきます。

まず結論を一言で言うと、0で割ってはいけない理由は「定義できない」または「計算できない」です。これだけだとわかりにくいと思うので、文字を用いて説明していきましょう。

n÷0 (n≠0) を考える

計算から考える

$${0\div0}$$はちょっと特殊なので後述します。まずは$${(0以外の数)\div0}$$を考えてみましょう。
$${n\div0  (n\neq0)}$$を式変形していくと下のようになります。ちょっと証明っぽくなっていますが、言っていることは至極当然のことです。

$$
n\neq0とする。\\
n\div0=x\\
n=x\times0\\
0に何を掛けても0になるので、n=0となる。\\
しかしこれは最初のn\neq0に反するため、n\div0は定義できない。
$$

グラフから考える

次にグラフから考えてみましょう。まずは下のグラフを見てください。

y=1/xのグラフ

これは反比例のグラフです。ここでは$${y=\frac{1}{x}}$$にしましたが、分子を変えても同じようなグラフが現れます。ここで、$${x=0}$$のときが0で割ることと等しくなります。では、その$${x=0}$$を考えてみますが、反比例のグラフはy軸($${x=0}$$)に限りなく近づいていても、完全に接するところはありません。つまり、グラフ上にx=0の地点は存在しないということです。本当にx=0がないのか？ということは下に簡単に示しておきます。

【反比例にx=0の地点がないことの説明】
x=0がないということは、下のグラフ($${y=\frac{1}{x}}$$)の赤で塗られたところの面積は∞になるということである。

(赤いところは実際は画面外まで続いている)

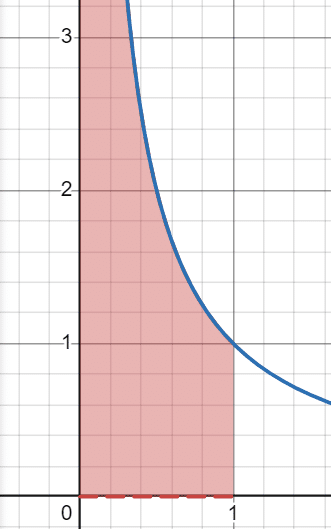
赤いところの面積を求めてみると、

$$
\int_0^1 \frac{1}{x}  dx\\
=[\log_ex]_0^1  (x\geq0)\\
=\log_e1-\log_e0\\
この場合は\log_e0=-\inftyとされているので、\\
\log_e1-\log_e0=\log_e1+\infty=\infty
$$

よって、$${y=\frac{1}{x}}$$のグラフにx=0の地点はない。

結局2つの考え方をまとめると、$${n\div0}$$はどんな値にもなりえない(結果が存在しない)ということです。このことを不能といいます。

0÷0を考える

次は$${0\div0}$$を考えていきます。まずは下のような式を考えてみましょう。

$$
1\div 1=1
$$

何をいまさらというような当たり前の式ですが、次はこれを変形していきます。

$$
0.1\div0.1=1\\
0.01\div0.01=1\\
0.001\div0.001=1\\
0.0001\div0.0001=1\\
0.00001\div0.00001=1\\
……
$$

このように、割る数、割られる数ともにどんどん0に近づけていっても割る数=割られる数なら当たり前ですが答えは1です。それなら$${0\div0=1}$$ということになる可能性もあります。しかし、次のような式も考えてみましょう。

$$
1\div0.1=10\\
0.1\div0.01=10\\
0.01\div0.001=10\\
……
$$

このように考えていくと、$${0\div0=10}$$となります。ここまでで勘の良い方は気づくと思いますが、0÷0はどんな数にでもなれます。つまり、$${0\div0=\pi}$$なんていう等式も考えられるということです。このように答えが複数あるようなことを不定といいます(不定積分の"不定"はこのことで、積分定数で答えが1つに定まらないため不定になっています)。

結論

まとめると、「0で割る」という行為は、答えが存在しない(不能)または答えが無数に存在する(不定)になってしまうため認められないということになります。

おまけ：もし0で割ることができたら？

最後におまけです。「0で割る」ことが許されたらどうなるのか？ということを見ていきましょう。
まずは割り算の定義ですが、割るということは逆数を掛けるということです。つまり、0で割るということは0の逆数を掛けるということになります。基本的に$${n}$$の逆数は$${\frac{1}{n}}$$なので、0の逆数を$${\frac{1}{0}}$$としてみましょう。逆数同士は掛けると1になるという性質があるため、$${0×\frac{1}{0}=1}$$が成り立つとします。ここで、下のような等式の変形を考えてみましょう。

$$
0=0+0\\
0\times\frac{1}{0}=(0+0)\times\frac{1}{0}\\
1=0×\frac{1}{0}+0×\frac{1}{0}\\
1=1+1\\
1=2
$$

なんと1=2というとんでもない等式が成立してしまいました。また、最初の式を$${0=0+0+0}$$にすれば$${1=3}$$、$${0+0+…+0  (0はn個)=0+0+…+0  (0はm個)}$$とすれば$${n=m}$$となってすべての数同士が等しいということになってしまいます。これでは基本演算どころか「数」という概念ですら崩壊しかねません。基本の四則演算ですら崩壊させる「0で割る」という行為は絶対に許されないということがよく分かりますね。