
アインシュタイン(23歳)の論文を読んでみよう
無名時代のアルくんの論文を読んでみようシリーズ、今回取り上げるのは1902年6月に投稿&受理された論文です。
"Kinetische Theorie des Wärmegleichgewichtes und des zweiten Hauptsatzes der Thermodynamik”(熱平衡の運動論と熱力学第二法則)
「熱力学第二法則」とあることからピンとくる方も多いと思います。エントロピーの法則が主題です。
ちなみに熱力学第一法則はエネルギー保存則のことです。第二がエントロピー増大の法則。
エネルギーとエントロピーの二つこそが、この物理宇宙を統べる二つのメーターであると、そんな風に理解してくだされば、これより繰り広げられるお話に十分ついていけると思います。


この「エントロピー」については、名前はよく見かけるけれどよくわからないと皆さん思われると思います。著名な割にはつかみどころがないですからね。ごく大雑把な説明をすると、例えばまんが家さんで、超クールな絵柄をさく裂させる方がいらっしゃって、当初は「あいつしか描けない!」と畏敬の念を抱かれるのだけど…

十数年経つとほかのまんが家さんたちがそのスタイルをそれぞれ消化していって、やがては前衛だったことさえ忘れられてしまう、そういう現象を「エントロピーの増大」と呼びます。
手塚治虫のスタイルもそうです。彼のまんがが出てきたとき、後にライヴァルとなる水木しげる先生は「日系二世か日米ハーフが描いているに違いない」と恐れおののいたそうですが…

その後いろいろな方々がこの絵柄をそれぞれ消化して、前衛どころか児童まんがのスタンダードに、さらには「今どきこの絵柄はないよねー」と見下されることさえ珍しくなくなったのでした。
頭一つ突き抜けていたものが、時とともにそうでなくなって、全体のなかの一部に取り込まれていく…そういうのを「エントロピーの増大」と思えば、ブツリガクの理解においてもたいてい間に合います。本当です、そうイメージしてください。
この「エントロピー増大」という現象については19世紀後半に何人かの学者によってそう名づけられていましたが、増大とは具体的にどんな風に増大するのか、うまく数式にのせるのが大変でした。それを説得力あるものまで育て上げたのが、イギリスのマクスウェルと、オーストリアのボルツマンでした。マクスウェルの名は目にしたことがあると思います。マクスウェル電磁気学ってジャンルがあるぐらいの巨匠だから。
ボルツマンは知名度ではかなり劣ってしまいますが、科学史における存在感はマクスウェルと同じかそれ以上です。彼の論文は数式の乱れ撃ちで、そして難解、平明に語る文才も今一つだったせいで、同時代にはなかなか理解されなかったのです。マクスウェルはボルツマン論文を読んでその真意を理解して、晦渋な部分を数式で整理してみせてボルさん感激なんてこともあったそうです。
さてこのボルツマンが1968年に、目を通すだけで頭が痛くなりそうな計算の果てに、興味深い法則にたどり着きました。気体が分子でできていると仮定して、それら分子がある熱の下にあるとき、どんな風にそれらが分布するかを、グラフ化できるような数式を捻りだしたのです。
先輩筋のマクスウェルがすでに、分子ではなく原子前提でしたがこの数式を1860年に提示していて、ボルツマンはそれに刺激されて8年後に、分子前提での数式を作ることに成功したわけです。

ここでアルくん登場です。23歳のときのことです。1902年、つまりボルやんの画期的研究より34年後にして、くだんのボル分布式に、とある思考実験によって一気にたどり着いたのです。いわゆる別解ですね。
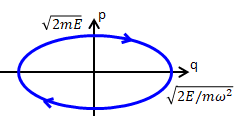
どういう解き方をしたのかというと…うーん「相空間」(phase space)と呼ばれる物理計算用の仮想空間を使ったのです。これは説明が難しいのですが要は「位置」と「運動量」の二つをメーターにすえれば、エネルギー保存則の下にある複数の(というか人間の感覚でいえば無数といっていい)質点の全体像を、楕円の周(下の図の青)として描けちゃうよーという優れものです。

この考え方はボルツマンも知っていたのですが、アルくんはこの楕円を、ひとつではなくN個あると仮定して、それをアニメのセル画を重ねるような感じ(検索セヨ)で重ねると、この楕円(の外周)にグラディエーションが生ずると切り出します。実際にそう彼が説明したのではないのですが私なりにイメージ言語に置きかえるとそんな風です。でもって、そのグラディエーションを積分すると、ボルツマン分布式があっさり出てくるよと、そう論証したのです。
ここ、ボルやんが論証にあたって苦労したところです。とある数学者より「その議論は穴がある、おかしい」と突っ込まれて彼は反撃しきれなかった、そういう難所がありました。後にそこが「エルゴード性」と名付けられたほどです。ところがアルくん、そういうめんどうな数学的議論のブラックホールには近寄らず、楕円を重ねてグラディエーションが~な議論をすることで、ボル分布式までたどり着いてみせたのでした。
もっとびっくりなのは、同じ1902年、アメリカのギブズが、同じ結論をアルくんとは違うやり方で提示していたことです。当時すでに巨匠で、故マクスウェルからも激賞されていたギブズさんがですよ。自分の妹の亭主が日本語研究者という縁で、彼の自宅には日本人留学生をいつも住まわせていたという、あのギブズ教授です。

『統計力学の基礎原理』(Elementary Principles in Statistical Mechanics)という教科書を、彼は1902年に刊行しました。同年3月だから、アルくんが満23歳を迎える頃ですね。この本のなかで、やはりボルツマン分布式を、彼の長年の研究に基づくやり方で導出していたのです。アルはこの本のことは当時タイトルも知らなくて、彼の必殺技である思考実験の積み重ねで、同じ解き方を、違うやり方で論文にしていたのでした。
余談ですがギブズ先生は翌1903年に亡くなっています。アルベルト・アインシュタインのその後の高名を知ることなく亡くなったことになりますね。もし彼が1902年当時のアルくんの論文(ちなみにドイツ語)を読んでいたら、どう思われたのか、私はひじょ~に想像をかきたてられます。
このふたり、ともに「リウヴィルの定理」を使っていました。イギリスの神童・ハミルトンの光学研究より発展した「ハミルトン力学」に、この定理を持ち込むと、すっげーことができると気づいたのはギブズ先生のほうが先でした。1884年の論文。ちなみにアルくんは当時5歳です。
それが1902年になって、ギブズとアルくんが、ほとんど同時にこの定理を使って、前者は数学的議論の積み重ねで、後者はもっとストレートな思考実験によって、ボルツマン分布式のスマートな導出法を発見したのでした。
思考実験について説明すると、「重いものほど落下速度が速くなる」という主張に反論する時、こんな風にするのがその一例ですね。「10キロのダンベルに、さらに10キロのダンベルを紐で括りつけて合計20キロにして、がけから落っことしたら、10キロのダンベルより二倍速く落ちると、あなたはお考えなのですか?」

こういう素朴な脳内シミュレーションを、アルくんは得意としていました。これを使いこなすと、めんどくさい計算を省いて一気に結論まで行けるのです。
"Kinetische Theorie des Wärmegleichgewichtes und des zweiten Hauptsatzes der Thermodynamik”(熱平衡の運動論と熱力学第二法則)は、そういう論文です。全17頁。

数式は色々出てはくるのだけど、式より文のほうが多いのですよ。

そうでないページもありますけどね。

これが最終頁です。

かっこよく締めくくっています。最終段落のみ日本語訳すると…
§10 第二法則の拡張。
ポテンシャルV aに対応する力の性質については何も仮定する必要はなく、そのような力が自然界に存在することさえ仮定する必要はない。したがって、熱の力学的理論は、カル ノーの原理を、任意の V を導入することによって観測された過程から生成できる理想的な過程に適用した場合に、正しい結果に到達することを要求している。もちろん、これらの過程を理論的に観察して得られた結果は、理想的な助力Vがその過程にもはや存在しない場合にのみ、真の意味を持つ。
翌1903年、この論文を足掛かりに、さらに大胆なことを彼は論じます。今回取り上げた論文は、気体に関する議論でした。それが翌年の論文では、気体に限定しないで同じ議論ができると議論するのです。
エントロピー増大の法則を、ある三つの仮定に基づいて応用すれば、それができる、と。
後日、気が向いたら紹介しますね。
この記事が気に入ったらサポートをしてみませんか?
