【熱力学６】熱力学とルジャンドル変換【美しい熱力学】

熱力学は非常に美しい理論を成しています．温度$${T}$$と外部変数の組$${X}$$の関数で表された自由エネルギー$${F(T,X)}$$さえ与えられれば，状態に関する完全な情報を持っており，理論が閉じるからです．というのも，自由エネルギーの外部変数での偏微分によって外部変数に共役な力$${x}$$（たとえば圧力のような）が求まるし，温度での偏微分によって状態の序列の指標となるエントロピー$${S}$$が求まるので，自由エネルギーは状態を完全に特徴づけているのです．数式としてもう一度書くと

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\begin{align*}
\pd{F(T,X)}{X_i} = x_i(T,X)\\
\pd{F(T,X)}{T} = S(T,X)
\end{align*}
$$

ということでした．このように，平衡状態の系に関する完全な情報を持っている関数のことを熱力学ポテンシャルと呼びます．（注: 呼び方にはいろいろな流儀があるようです．基本関係式とか完全な熱力学関数などとも呼ばれます．ギブズは自身の論文でfundamental functionと呼びました．）

それでは，温度と外部変数の組の関数として表されたエネルギーはどうでしょうか？また，これまで温度と外部変数で状態を指定してきたわけですが，他の変数で状態を指定したいときも，対応する熱力学ポテンシャルはあるでしょうか？これを今回は探っていきましょう．（今回の話は，理論の整備の意味合いが強く，あまり実用的ではないでしょうが，熱力学の美しさを味わえるので，個人的には大好きな話です．）

エネルギー方程式

５節「エントロピー」でつぎの式が得られました．

$$
\begin{align*}
E(T,X) = F(T,X) + TS(T,X)
\end{align*}
$$

これを外部変数で偏微分すれば，

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\begin{align*}
\pd{E(T,X)}{X_i} &= \pd{F(T,X)}{X_i} + T\pd{S(T,X)}{X_i}\\
&=x_i(T,X) - T\pd{x_i(T,X)}{T}
\end{align*}
$$

となることがわかります．この式はエネルギー方程式と呼ばれます．ここで，二行目でマクスウェルの関係式を用いています．

右辺に二項目の余分な項が付くのが，自由エネルギーの偏微分の形と違うところです．エネルギーは自由エネルギーと違って，別に温度一定の環境での仕事として定義されていないので，これは当然です．

ここでもしも，外部変数に共役な力が温度に比例するような形をしていると，右辺はゼロになります．すると，エネルギーの偏微分から力の情報を得ることができないという困ったことになります．たとえば，理想気体を考えましょう．理想気体とは，温度と密度に圧力が比例するような気体のことで，希薄な気体ではそのように振る舞うことが知られています．理想気体の圧力が温度に比例することから，理想気体については

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\begin{align*}
\pd{E(T,X)}{V} = 0
\end{align*}
$$

が成り立ちます．これは理想気体のエネルギーは体積によらないという，ジュール（Joule）の法則と呼ばれる良く知られた結果です．しかし，このことが意味するのは，エネルギーを温度と外部変数の関数として表した式からは，圧力の情報を知ることができない，という少し残念な結果です．

この意味で，温度と外部変数の関数としてのエネルギーは，同じ変数を用いた自由エネルギーよりも，持っている情報が少ないのです．

変数の取り換え

１節「状態の指定，温度とは」を思い出すと，温度で状態を指定することにしたのは，エネルギーの出入りがあるような着目系でも，温度なら環境によって一定に制御できるということからでした．もともとエネルギーの代わりに温度を用いたわけで，温度は全エネルギーから導かれる量だったわけです．したがって，エネルギーの変数に温度を使うということは，自分自身の情報を使って自分を記述しているようなものであって，情報の詳しさを損なうのは当たり前ともいえます．

それでは，初心に帰って，温度の代わりにエネルギーで状態を指定するとどうなるか考えてみましょう．このために，温度とエネルギーの間で成り立っているはずの関係$${T = T(E,X)}$$を，

$$
\begin{align*}
F(T,X) = E(T,X) - S(T,X) T
\end{align*}
$$

に代入して変数を温度からエネルギーに取り替えてみましょう．その結果は単純に，

$$
\begin{align*}
F(E,X) = E - S(E,X) T(E,X)
\end{align*}
$$

と書くことができましょう．しかし，こうして表された自由エネルギーは，もはや完全な情報を持っていません．もともと，自由エネルギーはギブズ・ヘルムホルツの式に頼って温度依存性が決定されていました．ギブズ・ヘルムホルツの式を再掲すると，

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
-T^2 \pd{}{T}\lr{\frac{F(T,X)}{T}} = E(T,X)
\end{align*}
$$

です．自由エネルギーの偏微分から導かれるものを自分自身に代入しているので，情報が失われるのです．自由エネルギーにとっての自然な変数は温度であって，決してエネルギーではないのです．

ルジャンドル変換

今の「エネルギー表示の自由エネルギー」の式を少し変形してみて，

$$
\begin{align*}
S(E,X) = -\frac{F(E,X)}{T(E,X)} + \frac{E}{T(E,X)}
\end{align*}
$$

としましょう（単に温度で割って整理しただけです）．ここから議論することも全く構わないのですが，少し式が見づらいので，式を平べったく書くために，温度表示の（本来の熱力学ポテンシャルとしての）自由エネルギーに関して

$$
\begin{align*}
B &= \frac{1}{T}\\
\mathcal{F}(B,X) &= - B F(B,X)
\end{align*}
$$

と置き換えることにします．これらには一応名前があって，$${B}$$は逆温度，$${\mathcal{F}(B,X)}$$はマシュー（Massieu）関数と呼ばれたりします．このマシュー関数は自由エネルギーを単に書き換えただけなので，熱力学ポテンシャルです．マシュー関数を用いると，ギブズ・ヘルムホルツの式は

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\begin{align*}
\pd{\mathcal{F}(B,X)}{B} = -E(B,X)
\end{align*}
$$

と書かれ，先ほどの式も

$$
\begin{align*}
S(E,X) = \mathcal{F}(E,X) + E B(E,X)
\end{align*}
$$

となって見やすくなります．この式の右辺第二項をギブズ・ヘルムホルツの式によって書き換えると，

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\sbs}[1]{\left. #1 \right|}
\begin{align*}
S(E,X) = \mathcal{F}(E,X) - \sbs{\pd{\mathcal{F}(B,X)}{B}}_{B=B(E,X)} B(E,X)
\end{align*}
$$

であることがわかります．これは，数学的にはルジャンドル（Legendre）変換と呼ばれる形をしています．ルジャンドル変換とは，変数を変換する数学的操作ですが，凸関数ならその情報が失われないという特徴があります．これは，「座標の組でも関数を再現できるが，接線の傾きと切片の組でも関数を再現できる」ということに基づく変換で，図形的なイメージは次の通りです．

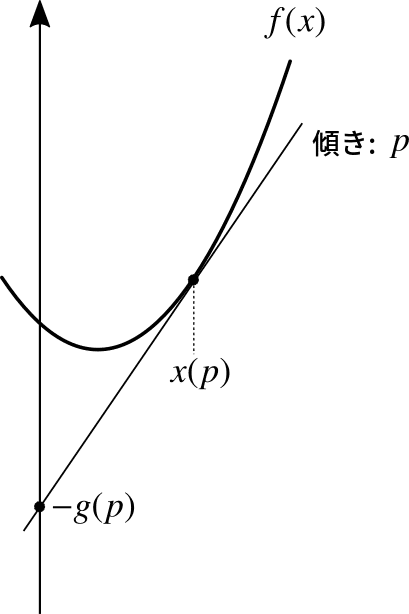
この図では，$${(x,f(x)) \to (p,g(p))}$$という変換をしています．もとの関数に接線を引き，その接線の切片を，そのときの傾きとともに記録するのです．これと同様で，先の式も$${(B,\mathcal{F}(B,X)) \to (E,S(E,X))}$$という変換をしたことになってます．つまり，「逆温度を変数とするマシュー関数」のルジャンドル変換として，「エネルギーを変数とするエントロピー」が得られたことになります．

ルジャンドル変換では情報が失われないので，エネルギーと外部変数で表されたエントロピーは完全な情報を持った熱力学ポテンシャルであるといえます．

また，この熱力学ポテンシャルとしてのエントロピーはエネルギーについて単調であることが簡単にわかるので，逆に解くことができて，

$$
\begin{align*}
E = E(S,X)
\end{align*}
$$

という関数を得ることもできます．熱力学ポテンシャルを逆に解いただけなので，これも熱力学ポテンシャルであることは明らかでしょう．温度と外部変数で指定されたエネルギーは熱力学ポテンシャルではないのに対し，エントロピーと外部変数で指定されたエネルギーは熱力学ポテンシャルなのです．

実は，関数にとって何が自然な変数であるのかということにはもう少し簡単な判定法があります．前回の完全微分の形にヒントがあって，エネルギーの完全微分は

$$
\begin{align*}
dE &= \sum_i x_i dX_i + d'\varphi\\
&= \sum_i x_i dX_i + TdS
\end{align*}
$$

と書けます．この式は実際にエネルギーの自然な変数がエントロピーと外部変数であることを示しています．

実用性は？

熱力学ポテンシャルはルジャンドル変換で結びついているので，どれも等価な情報を持っています．したがって，理論上は好きなものを使えばよいのです．

ところが，私たちの測定で実際に得られるのは，エントロピーと外部変数で指定されたエネルギーではなく，温度と外部変数を制御して得られるエネルギーです．エントロピーを制御することは困難ですし，直接測ることもできません．よって，エントロピーを自然な変数に用いる方法は実用性の面では優れていません．そのため私は，ヘルムホルツの自由エネルギーを基礎にして熱力学を特徴づけるような論理展開でここまで進めてきたのです．しかしながら，このような数学的な構造が背景にあることは面白く，エントロピーという関数に深い意味があることがわかります．また，エントロピーを自然な変数に用いると，示量変数だけで状態を指定できるので，状態の指定の仕方を直接的に細かくできているという特長もあり，数学的にはエントロピーは取り扱いやすいのです．（ちなみに，普通の教科書ではエントロピーが先に出てきて，エントロピーだと実用上使いづらいから自由エネルギーにルジャンドル変換するという流れをとります．私は普通と逆方向のことをしていてマニアックだと思われるかもしれませんが，私のノートでは自由エネルギーを先に与えているので，この流れで熱力学ポテンシャルとしての自由エネルギーとエントロピーの等価性を示しました．）

また，実は応用面ではヘルムホルツの自由エネルギー以上に便利な熱力学ポテンシャルもあります．体積ではなく，圧力を制御して実験をすることの方が多いので，圧力で状態の指定をしたいことは多いわけです．そのためにはどうしたらよいでしょうか．それはやはりルジャンドル変換によって変数を取り換えればよいのです．

今回のまとめ

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

更新履歴
Mar. 6, 2020 本質的には変わりませんがマシュー関数の定義で符号が間違っていたので修正しました．