
ちょっと珍しいa(z+1/z)+b型関数
この記事は日曜数学 Advent Calendar 2023の3日目の記事です。
どうも、108Hassiumです。
タイトル通り、$${f(z)=a(z+\frac{1}{z})+b}$$という形の関数の中からちょっと珍しい性質を持つものを紹介したいと思います。
前提知識
本題に入る前に、前提知識の説明をさせてください。
以下の記事を読了済みであり、内容を完璧に覚えていると断言できる方は読まなくても大丈夫です。
ジュリア集合
$${z_0=\alpha}$$として$${z_{n+1}=f(z_n)}$$という数列を計算し、発散・収束速度などに応じた色で複素平面上に$${\alpha}$$をプロットすることで得られる図形を「$${f(z)}$$のジュリア集合」と呼ぶことにする。
wikipedia等に載っている(おそらく正式であろう)定義とは異なりますが、利便性等の都合によりこちらの定義を使用します。
同値な言いかえですらない完全な別物ですが、この記事では厳密な数学数学した議論をするわけではないのでこれで通します。
ジュリア集合と聞くと、以下のような「$${z^2+c}$$のジュリア集合」を思い浮かべる方が多いと思います。



$${z^2+c}$$のジュリア集合は、$${z_n}$$が固定点や周期サイクルに収束する領域と無限大に発散する領域でできています。(本当は各領域の境界線上に特殊な性質を持つ点が集まっているのですが、この記事では無視することにします)
以下、$${z_n}$$が無限大に発散する領域を「発散領域」、収束していく領域を「収束領域」と呼ぶことにします。
ちなみに$${z^2+c}$$のジュリア集合は、$${c}$$の値によっては以下のように収束領域が存在しなくなることもあります。

$${z^2+c}$$のジュリア集合は無限遠まで広がる発散領域の中にポツンと収束領域が存在している(ない場合もある)構造になっていますが、これは$${z^2+c}$$に限らず2次以上の多項式関数全般に共通する特徴です。
一方で多項式関数でない有理関数(多項式÷多項式で表せる関数)、例えば$${\frac{1}{z^2}+c}$$のジュリア集合はこんな形をしています。



複素平面全体が収束領域になり、複雑な曲線で領域が分割されています。
マンデルブロ集合
$${z_0=\alpha}$$として$${z_{n+1}=f(z_n,c)}$$という数列を計算し、発散・収束速度などに応じた色で複素平面上に$${c}$$をプロットすることで得られる図形を「($${\alpha}$$を初期値とする)$${f(z,c)}$$のマンデルブロ集合」と呼ぶことにする。
ジュリア集合とは異なり、マンデルブロ集合は2変数の関数で定義される概念で、さらに初期値にも依存しています。



マンデルブロ集合もジュリア集合と同じく$${z_n}$$が発散する領域と収束する領域に分かれているので、それぞれ発散・収束領域と呼ぶことにします。
ジュリア集合とマンデルブロ集合の関係
初期値を適切に決めることで、マンデルブロ集合からジュリア集合に関する情報を読み取ることができます。
例えば$${z^2+c}$$の$${z_0=0}$$のマンデルブロ集合からは、$${z^2+c}$$のジュリア集合の収束領域の有無が読み取れます。

定数$${c}$$がマンデルブロ集合の収束領域の中にあれば$${z^2+c}$$のジュリア集合は収束領域を持ち、発散領域の中にあれば収束領域を持たないようです。
説明は面倒なので省略しますが、収束領域の有無以外にも枝分かれの仕方、尖り具合や曲がり具合、発散領域の模様の細かさなどの外見的特徴もマンデルブロ集合から読み取れる場合があります。
このような性質を利用して、私は特定の形の関数のジュリア集合の中から面白いものを見つけ出したいとき、まず最初にマンデルブロ集合を描画してみてそれを見ながらジュリア集合のパラメータを調整する、という事をよくやっています。
そして理由は不明なのですが、どうやら初期値が「$${f(z,c)}$$の$${z}$$についての臨界点(微分係数が0になる点)」であるときに$${f(z,c)}$$のマンデルブロ集合はこのような性質を持つらしいです。
実際に$${z^2+c}$$を$${z}$$で微分すると$${2z}$$になり、$${z=0}$$のときは$${2z=0}$$になっています。
企画概要
$${f(z)=a(z+\frac{1}{z})+b}$$という形の関数は、$${z=1}$$と$${z=-1}$$という2つの臨界点を持ちます。
そのため、($${a,b}$$を$${c}$$の関数として)$${a(z+\frac{1}{z})+b}$$のマンデルブロ集合からジュリア集合の情報を得ようにも2種類のマンデルブロ集合ができてしまいます。
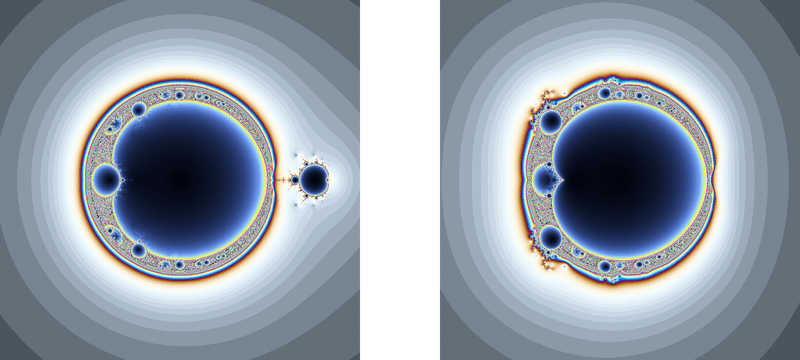

こういった場合はどちらか一方が正解というわけではなく、2つのマンデルブロ集合の情報を同時に調べることでジュリア集合の情報(収束領域の存在・形状など)が見えるようになる場合が多く、そのような状況はジュリア集合を楽しむうえでは少しだけ面倒です。
しかし、例えば一方のマンデルブロ集合が何の情報も持っていなかったり、2つのマンデルブロ集合が全く同じ形だったりすると、1個のマンデルブロ集合だけから$${a(z+\frac{1}{z})+b}$$のジュリア集合の情報が得られることになります。
このような「マンデルブロ集合が実質1種類しかない$${a(z+\frac{1}{z})+b}$$型関数」こそが表題の「ちょっと珍しい[略]関数」で、この記事ではそのような関数の具体例をたくさん紹介したいと思います。
ちなみに、そもそもなぜ$${a(z+\frac{1}{z})+b}$$という形の関数に着目したのかというと、単にこの形の関数が「臨界点が2個しかない有理関数」の中でもシンプルな形の関数だからです。
同様な性質を持つ関数としては3次関数がありますが、3次関数では以下の通りすでに同じ調査を行っているので今回は$${a(z+\frac{1}{z})+b}$$を選んだというわけです。
f(1)=-1
$${f(1)=-1}$$が成り立つと、$${z_0=1}$$の数列は$${z_0=-1}$$の数列と同じ値が並ぶことになる、つまり全く同じ挙動になるので計算する必要が無くなります。
$${f(z)=c(z+\frac{1}{z})+d}$$とすると、$${f(1)=-1}$$という方程式は$${2c+d=-1}$$と表せます。
この式を$${d}$$について解いて$${f(z)}$$の定義式に代入して少し整理すると、$${f(z)=c(z+\frac{1}{z}-2)-1}$$という関数が得られます。

中央の円より外側が$${z_n}$$が発散していく領域で、円の内側にある青や黄色の領域は$${z_n}$$が周期数列に収束していく領域、その他のモザイク状の模様の部分はカオス的挙動を示す領域(途中で大きい値になるので発散したと判定されている)です。

$${z_0=1}$$の方のマンデルブロ集合を描画してみると、確かに$${z_0=-1}$$のものと同じ形になっています。

ジュリア集合は以下のような感じです。




f(1)=1
$${c}$$の値に関係なく常に$${f(1)=1}$$が成り立つ場合、$${z_0=1}$$の数列は常に1に収束することになるので計算する必要が無くなります。
先程と同様に$${f(z)=c(z+\frac{1}{z})+d}$$として立式して解くと、$${f(z)=c(z+\frac{1}{z}-2)+1}$$という解が得られます。

$${z_0=1}$$とすると収束先も収束速度もどこでも同じなので、マンデルブロ集合は何の模様もないまっさらな画像になります。

ジュリア集合はこんな感じです。



暗い青色の領域が1に収束するような初期値に、その他の明るい色の領域が$${z_0=-1}$$の数列と同じサイクルに収束する初期値に対応しています。

これは$${z_0=-1}$$でも1に収束する場合のジュリア集合で、色の違いは収束速度の違いを表しています。
ところで、$${c(z+\frac{1}{z}-2)+1}$$のジュリア集合の「1に収束する領域が$${z_0=-1}$$のサイクルに収束する領域を囲んでいる」という性質は、「1に収束する領域」を「発散領域」に置き換えると多項式関数のジュリア集合と似ていることがわかります。
実は、$${c(z+\frac{1}{z}-2)+1}$$のジュリア集合は以下のようにして$${z^2+\gamma}$$という形の関数のジュリア集合と関連付けることができます。
まず$${f(z)=c(z+\frac{1}{z}-2)+1}$$とし、さらに$${h(z)=\frac{2}{2cz-1}+1}$$という関数を考えます。
そして、$${h^{-1}(f(h(z)))}$$($${h^{-1}(z)}$$は$${h(z)}$$の逆関数)を計算します。
$${h^{-1}(z)=\frac{1}{c(z-1)}+\frac{1}{2c}}$$なので、$${h^{-1}(f(h(z)))}$$は以下のようになります。
$${h^{-1}(f(h(z)))\\=h^{-1}(f(\frac{2}{2cz-1}+1))\\=h^{-1}(c(\frac{2}{2cz-1}+1+\frac{2cz-1}{2cz+1}-2)+1)\\=h^{-1}(c(\frac{2(2cz+1)+(2cz-1)^2-(2cz-1)(2cz+1)}{(2cz-1)(2cz+1)})+1)\\=h^{-1}(\frac{4c}{4c^2z^2-1}+1)\\=\frac{1}{c(\frac{4c}{4c^2z^2-1}+1-1)}+\frac{1}{2c}\\=\frac{4c^2z^2-1}{4c^2}+\frac{1}{2c}\\=z^2-\frac{1}{4c^2}+\frac{1}{2c}}$$
ここで$${-\frac{1}{4c^2}+\frac{1}{2c}=\gamma}$$と置くことで、$${h^{-1}(f(h(z)))}$$を$${z^2+\gamma}$$という形に変形できたことになります。(以下、$${g(z)=z^2+\gamma}$$とします)
2つの関数$${f(z)}$$と$${g(z)}$$の間に$${h^{-1}(f(h(z)))=g(z)}$$が成り立つような$${h(z)}$$が存在するとき、「$${f(z)}$$と$${g(z)}$$は位相共役である」というそうです。
位相共役であることに何の意味があるかというと、$${a_{n+1}=g(a_n)}$$という数列と$${b_0=h(a_0),b_{n+1}=f(b_n)}$$という数列の間に以下のような関係が成り立ちます。
$${a_1=g(a_0)=h^{-1}(f(h(a_0)))=h^{-1}(f(b_0))=h^{-1}(b_1)}$$
$${a_2=g(a_1)=h^{-1}(f(h(h^{-1}(b_1))))=h^{-1}(f(b_1))=h^{-1}(b_2)}$$
$${a_3=g(a_2)=h^{-1}(f(h(h^{-1}(b_2))))=h^{-1}(f(b_2))=h^{-1}(b_3)}$$
$${a_4=g(a_3)=h^{-1}(f(h(h^{-1}(b_3))))=h^{-1}(f(b_3))=h^{-1}(b_4)}$$
・・・という風に、常に$${a_n=h^{-1}(b_n)}$$が成り立ちます。
ということは、例えば$${a_n}$$が固定点へ収束すれば$${b_n}$$も固定点へ収束し、$${a_n}$$が周期サイクルに収束すれば$${b_n}$$も全く同じ長さの周期サイクルに収束し、$${a_n}$$がカオス挙動をするなら$${b_n}$$もカオスになる、といったように$${a_n}$$と$${b_n}$$は常に似たような挙動をすることになります。
そしてジュリア集合においては、枝分かれの仕方や収束領域の尖り具合・曲がり具合といった視覚的な特徴を共有することになります。




ちなみにマンデルブロ集合は全く同じ形になります。

z^2-1/(4c^2)+1/(2c)のマンデルブロ集合(z_0=0)
実はこのような性質は既に紹介した$${f(1)=-1}$$の関数にもあり、
$${h(z)=\frac{2\sqrt[3]{2c}}{z+\sqrt[3]{2c}}-1}$$
$${\gamma=-\frac{1}{\sqrt[3]{4c^2}}-\sqrt[3]{2c}}$$
・・・とすると、$${c(z+\frac{1}{z}-2)-1}$$は$${\frac{1}{z^2}+\gamma}$$と位相共役になります。
f(1)=0
$${f(0)=\infty}$$なので、$${f(1)=0}$$が成り立つなら$${z_0=1}$$の数列は常に発散することになるので計算する必要が無くなります。

中央の円の内側をよく見ると、所々に灰色の丸い模様が見られます。

前述の通りモザイク状の領域は$${z_n}$$がカオスになる領域なのですが、何故この関数のマンデルブロ集合では斑点模様が現れ、何故同じくモザイク状領域のある$${c(z+\frac{1}{z}-2)-1}$$では現れなのか、というのは今のところ謎です。




ジュリア集合に関しては、あまり目立った特徴はなさそうでした。
f(1)=f(-1)
$${f(1)=f(-1)}$$が成り立つと、$${f(1)=-1}$$のときと同じ理屈で$${z_0=1}$$の計算が要らなくなります。
しかし、$${f(z)=a(z+\frac{1}{z})+b}$$として方程式を立てると$${a=0}$$になってしまい、$${a=0}$$だと$${f(z)}$$は定数関数になってしまい面白くないので「解無し」として扱います。
なお、$${c(z+\frac{1}{z})+d}$$型関数の臨界点が実質1個しかないと見做せる条件としては「$${f(-1)=-1}$$」や「$${f(-1)=1}$$」等もあります。
しかし、1と-1の入れ替えで同じになる条件(例えば$${f(-1)=-1}$$と$${f(1)=1}$$、$${f(-1)=1}$$と$${f(1)=-1}$$など)から生成される関数のジュリア集合・マンデルブロ集合は同じ見た目になるっぽいので省略していきます。
f(f(1))=-1
$${f(1)=-1}$$と同じような、数列が合流してマンデルブロ集合が同じ形になるパターンです。
これまでに求めてきた関数を並べてみると、以下のようになります。
$${c(z+\frac{1}{z}-2)-1}$$
$${c(z+\frac{1}{z}-2)+1}$$
$${c(z+\frac{1}{z}-2)}$$
どの関数も$${a(z+\frac{1}{z})+b}$$ではなく$${a(z+\frac{1}{z}-2)+b}$$という形になっています。
こうなった理由は元々は「そのような形に整理でき、なおかつそうした方が見栄えが良かったから」というだけだったのですが、実はこの形にすると「$${f(1)}$$が簡単な式になり、計算が少し楽になる」というメリットがあります。
というわけで、$${f(z)=a(z+\frac{1}{z}-2)+b}$$と置いて$${f(f(1))=-1}$$を解いてみます。
$${f(f(1))+1\\=f(b)+1\\=a(b+\frac{1}{b}-2)+b+1=0}$$
$${a(b^2+1-2b)+b^2+b=0}$$
$${a}$$について1次、$${b}$$について2次になったので、$${a}$$について解いて$${b=c}$$とすることで$${f(z)=(-1-\frac{3c-1}{c^2-2c+1})(z+\frac{1}{z}-2)+c}$$という解が得られます。

今までのものとは大きく異なるシルエットのマンデルブロ集合になりました。




ジュリア集合に関しては、あまり面白い特徴はなさそうです。($${f(1)=-1}$$のときと同じく$${\frac{1}{z^2}+c}$$のジュリア集合に似ている気がするのですが、関連性は見つけられませんでした)
f(f(1))=1
$${f(1)=1}$$と同じような、数列が確定で収束するパターンです。
先程と同様に$${f(z)=a(z+\frac{1}{z}-2)+b}$$と置くことで、最終的に$${f(z)=c(z+\frac{1}{z}-2)+1-\frac{1}{c+1}}$$という解が得られます。
ちなみに$${f(z)=c(z+\frac{1}{z}-2)+1}$$という解もあるのですが、こちらは$${f(1)=1}$$の解として既に紹介したものと同一です。

$${f(1)=1}$$のものと似た、モザイク領域が無い円形のマンデルブロ集合ですが、$${f(1)=1}$$のものには無かった網目状の模様が見られます。




実はこの関数、$${h(z)=-\frac{2}{(2c+1)z+1}+1}$$、$${\gamma=\frac{8c(c+1)^2}{(2c+1)^3}}$$とすると$${\frac{\gamma}{z^2-1}+1}$$と位相共役になります。
「$${\frac{\gamma}{z^2-1}+1}$$って何だよ、そんな関数知らねーよ」と思った人もいるかと思いますが、これは私が個人的に好きな関数の一つです。
$${\frac{c}{z^2-1}+1}$$はジュリア集合もマンデルブロ集合も非常に特徴的で、私の記事の中でもことあるごとに触れています。

ところで、最初に位相共役の説明をした時からずっと、$${h(z)}$$をどうやって見つけたのか気になっている人もいると思います。
これに関しては上手い方法が思い付かず、かといって計算力でゴリ押しすることもできなかったので以下のような方法を使いました。
$${h_1(x)=\frac{b}{x+a}+d}$$とし、グラフ描画ツールで$${h_1^{-1}(f(h_1(x)))}$$のグラフを描画する。
$${a}$$、$${b}$$、$${d}$$の値を動かし、$${h_1^{-1}(f(h_1(x)))}$$のグラフが$${g(x)}$$のグラフと似た形になるようなパラメータの組み合わせを見つける。
$${f_2(x)=h_1^{-1}(f(h_1(x)))}$$、$${h_2(z)=jx+k}$$とし、$${h_2^{-1}(f_2(h_2(x)))}$$が$${g(x)}$$と同じ形になるような$${j}$$、$${k}$$を求める。
$${h(z)=h_1(h_2(z))}$$とする。
$${f(x)=c(x+\frac{1}{x}-2)+1-\frac{1}{c+1}}$$、$${g(x)=\frac{\gamma}{x^2-1}+1}$$の場合、まず$${(a,b,d)=(0,1,1)}$$とすると$${h_1^{-1}(f(h_1(x)))}$$のグラフが($${c}$$に依存せず常に)$${g(x)}$$のグラフと似た形になりました。

この値で$${h_1^{-1}(f(h_1(x)))}$$を計算すると$${\frac{c(c+1)^2}{(x-c)(x+c+1)}-c-1}$$となり、これを$${f_2(x)}$$とします。
次に$${h_2(z)=jx+k}$$として$${h_2^{-1}(f_2(h_2(x)))}$$を計算し、
分母が$${x^2-1}$$の定数倍になる
定数項が1になる
・・・という条件を満たす$${j}$$と$${k}$$の組み合わせを求めます。
そして最後に$${h_1(h_2(x))}$$を計算すれば$${h(x)}$$が求まり、$${h^{-1}(f(h(z)))}$$を計算すれば$${\gamma}$$も算出できます。
この方法(特に手順1)が上手くいく根拠は全く無かったので、3回連続で成功したのは私目線ではほぼ奇跡です。
f(f(1))=0
$${f(1)=0}$$と同じような、数列が確定で発散するタイプです。
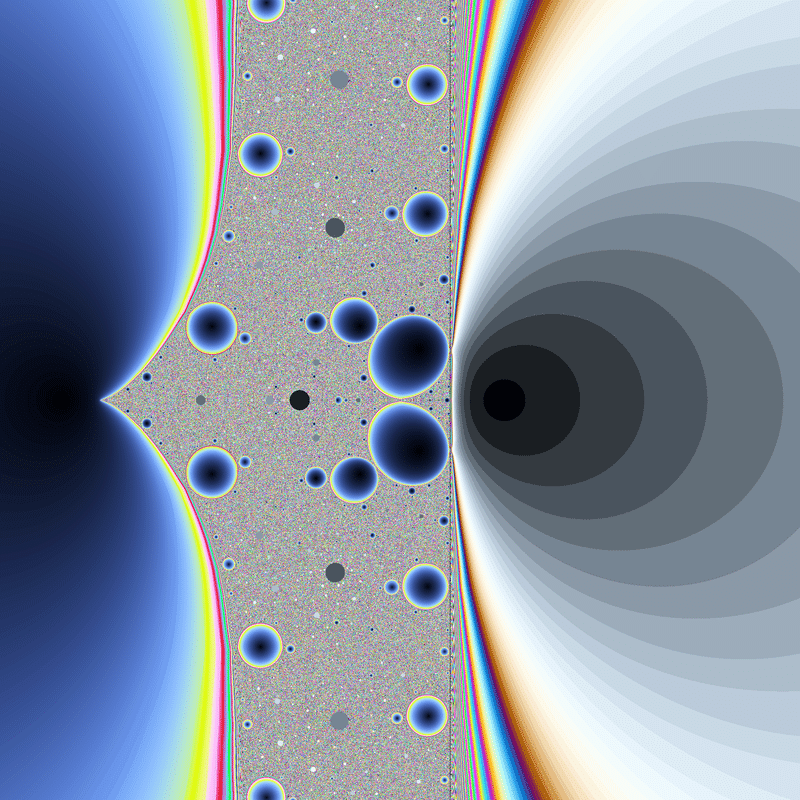
$${f(1)=0}$$のときと同様に、モザイク状の領域の中に灰色の斑点が現れています。



ジュリア集合については特に面白い特徴はなさそうです。
f(f(1))=f(1)
$${f(1)=1}$$や$${f(f(1))=1}$$と同じような確定収束パターンですが、残念ながら紹介済みのものと異なる解はなさそうでした。
$${f(z)=a(z+\frac{1}{z}-2)+b}$$として$${f(f(1))-f(1)}$$を計算すると、
$${f(f(1))-f(1)\\=f(b)-b\\=a(b+\frac{1}{b}-2)\\=\frac{a}{b}(b^2+1-2b)\\=\frac{a}{b}(b-1)^2}$$
・・・となり、$${f(f(1))-f(1)=0}$$の解は$${a=0}$$か$${b=1}$$しかないようです。
また、$${f(f(1))=f(-1)}$$も同様に既知の解しか存在しないようでした。
f(f(1))=f(f(-1))

巨大な楕円状の概形のマンデルブロ集合ですが、よく見ると真ん中に穴が開いていてドーナツ状になっています。

ジュリア集合はこんな感じです。



あまり目立った特徴はなさそうです。


今までの例では紹介していませんでしたが、$${c}$$がマンデルブロ集合の発散領域にあるときはこんな感じのジュリア集合になります。
この関数の場合、$${c}$$が楕円の外側にあるときと内側の穴の中にあるかで目立った違いはなさそうです。
f(f(f(1)))=-1
関数の合成回数が多い条件になってくると、「方程式が複雑すぎて$${a}$$と$${b}$$を$${c}$$についての有理関数として表せなくなる」という事態が発生します。
$${f(f(f(1)))=-1}$$($${f(z)=a(z+\frac{1}{z}-2)+b}$$)の場合、$${a}$$と$${b}$$の方程式にすると以下のようになります。
$${a(a(b-1)^2+b^2-b)^2+(b^2+b)(a(b-1)^2+b^2)=0}$$
$${a}$$について3次、$${b}$$については4次という恐ろしい方程式になってしまい、置換や因数分解といった道具が通用しなかったので「解けない」と判断しました。
同様に、$${f}$$の合成回数が3回までのものについては以下の4本が解けないものと判断しました。
$${f(f(f(1)))=1}$$
$${f(f(f(1)))=0}$$
$${f(f(f(1)))=f(f(-1))}$$
$${f(f(f(1)))=f(f(f(-1)))}$$
高次方程式については私は全くの素人(?)ですので、もしかしたらこの中に本当は解けるようなものが混ざっているかもしれません。
$${f(z)=\frac{ab-b^2}{b^2-2b+1}(z+\frac{1}{z}-2)+b}$$と置いたりすると$${f(f(1))=0}$$とかはかなり惜しい感じになるので、良かったらぜひチャレンジしてみてください。
f(f(f(1)))=f(1)
こちらは既知の解と同じ物しか存在しないパターンです。
どうやら一般に、$${f^{n}(1)=f(1)}$$($${f^n(z)}$$は$${f(z)}$$の$${n}$$重合成関数)はより合成回数の少ない条件式に対応する解しか持たないようです。
実際に、$${f(z)=a(z+\frac{1}{z}-2)+b}$$とすると$${f^n(1)-f(1)}$$は以下のように変形できます。
$${f^n(1)-f(1)\\=a(f^{n-1}(1)+\frac{1}{f^{n-1}(1)}-2)+b-b\\=\frac{a}{f^{n-1}(1)}(f^{n-1}(1)-1)^2}$$
よって、$${f^n(1)-f(1)=0}$$は$${f^{n-1}(1)-1=0}$$、つまり$${f^{n-1}(1)=1}$$と同じ解しか持たないことがわかります。
これと同様に、$${f^n(1)=f(-1)}$$も$${f^{n-1}(1)=-1}$$と同じ解しか持たないようでした。
f(f(f(1)))=f(f(1))
$${f^3(1)}$$系の方程式の中で唯一残った$${f(f(f(1)))=f(f(1))}$$には、$${f(z)=c(z+\frac{1}{z}-2)+1-\frac{2}{c+1}}$$という解がありました。($${f^4(1)}$$が出てくるものに関しては、新たな解は一つも見つけられませんでした)
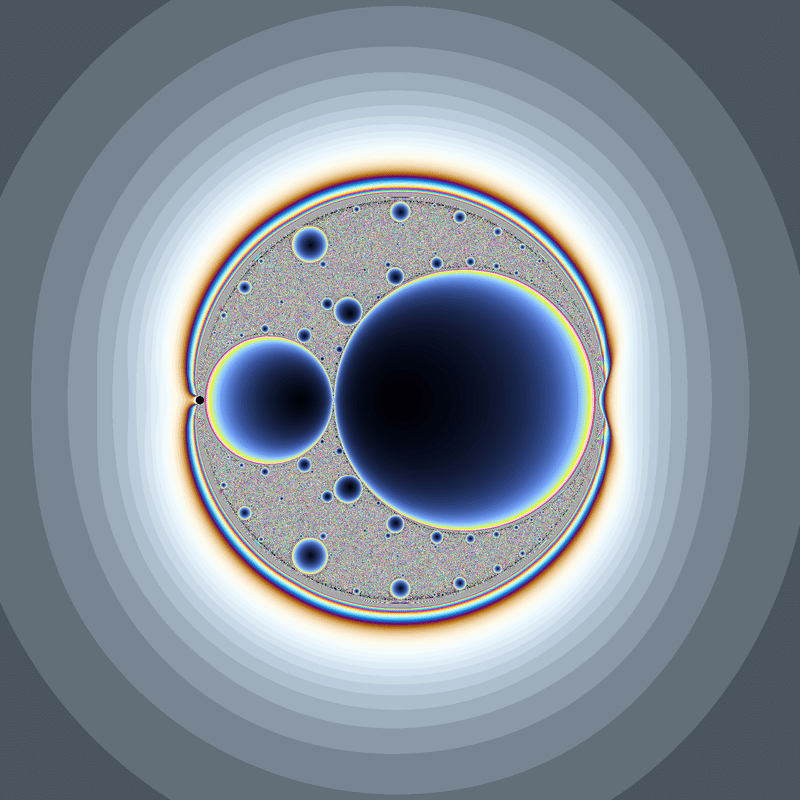
中央の円の左端に謎の黒い丸がありますが、おそらく計算精度に関する不具合による描画ミスです。



その他
今までのものと少し毛色の違う関数として、$${f(z)=c(z+\frac{1}{z})}$$があります。

$${h(z)=-z}$$とすると$${h^{-1}(f(h(z)))=f(z)}$$が成り立ち、さらに$${h(1)=-1}$$も成り立っています。
よって$${z_n}$$の挙動(収束・発散性や周期など)は$${z_0=1}$$と$${z_0=-1}$$のときで同じになり、マンデルブロ集合も同じ見た目になります。

ジュリア集合はこんな感じです。


赤が$${z_0=1}$$、緑が$${z_0=-1}$$と同じサイクルに収束する領域です。
ちなみに私のnoteのアイコン画像は$${(0.81+0.4i)(z+\frac{1}{z})}$$のジュリア集合です。


$${z_0=\pm1}$$の数列は必ずしも別々のサイクルに収束するわけではなく、同じサイクルに収束して1色のジュリア集合になることもあるようです。




$${c=\pm x+iy}$$のジュリア集合は収束領域の輪郭だけ見れば同じ形(鏡像)になっているようですが、色の別れ方は一致しないこともあるようです。
さて、この手の関数を求めるには今までのものとは少し違った計算が必要になります。
例として、$${f(z)=a(z+\frac{1}{z})+b}$$、$${h(z)=jz+k}$$として$${h^{-1}(f(h(z)))=f(z)}$$を満たすような関数の組み合わせを探してみます。
まず$${h^{-1}(f(h(z)))=f(z)}$$を$${f(h(z))=h(f(z))}$$と変形し、両辺を展開します。
$${f(h(z))=f(jz+k)=a(jz+k+\frac{1}{jz+k})+b}$$
$${h(f(z))=h(a(z+\frac{1}{z})+b)=aj(z+\frac{1}{z})+bj+k}$$
それぞれ$${z(jz+k)}$$を掛けて分母を払います。
$${z(jz+k)(a(jz+k+\frac{1}{jz+k})+b)\\=z(a((jz+k)^2+1)+b(jz+k))\\=z(a(j^2z^2+2jkz+k^2+1)+bjz+bk)\\=z(aj^2z^2+(2ajk+bj)z+ak^2+a+bk)\\=aj^2z^3+(2ajk+bj)z^2+(ak^2+a+bk)z}$$
$${z(jz+k)(aj(z+\frac{1}{z})+bj+k)\\=(jz+k)(aj(z^2+1)+z(bj+k))\\=(jz+k)(ajz^2+(bj+k)z+aj)\\=aj^2z^3+(bj^2+jk)z^2+aj^2z+ajkz^2+(bjk+k^2)z+ajk\\=aj^2z^3+(bj^2+jk+ajk)z^2+(aj^2+bjk+k^2)z+ajk}$$
この2つが常に等しくなるためには、$${z^3}$$~$${z^0}$$までの係数が全て等しくなければなりません。
というわけで、以下のような連立方程式を解くことになります。
$${\begin{cases}2ajk+bj=bj^2+jk+ajk\\ak^2+a+bk=aj^2+bjk+k^2\\0=ajk\end{cases}}$$
これの解法は省略しますが、最終的に$${h(z)}$$も$${f(z)}$$も定数関数にならず、なおかつ$${h(1)=-1}$$も成り立つような組み合わせは「$${f(z)=a(z+\frac{1}{z})}$$、$${h(z)=-z}$$」しか見つかりませんでした。
また、$${h(z)}$$が1次関数ではなく$${\frac{kz+l}{z+j}}$$という形になるケースも計算してみたのですが、膨大な量の計算の末に1個も解が見つからなくてキレそうになりました。(他の所での$${h(z)}$$の計算で変なやり方をしていたのはこれが原因です)
他にも$${h(z)}$$が2次関数のケースや$${f(f(h(z)))=h(f(f(z)))}$$みたいな条件も考えられるのですが、条件を少し複雑にするだけで連立方程式の本数が急激に増えるので面白い解は見つからないんじゃないかと思います。
最後に
明日の日曜数学 Advent Calendar 2023の記事は、integers_blogさんの担当です。
本稿執筆時点(2023/12/02/1:39)での概要は「まずは登録することが大事」とのことですが、一体どんな記事になるんでしょうか?
追記(2023/12/05)
「解けそうで解けない」と紹介した$${f(f(f(1)))=0}$$を解く($${a,b}$$を$${c}$$の有理式で表す)ことに成功しました。







$${f(f(f(1)))=0}$$を解くには、まず$${g(z)=\frac{(a-b)(b+1)z^2}{b^2(z+1)}+b}$$と置きます。
この式だけ見ると意味不明だと思いますが、これには以下のような意味があります。
まず、$${\frac{az^2}{z+1}+b}$$という形の関数は$${a(z+\frac{1}{z}-2)+b}$$とよく似た関数で、例えばグラフを見比べてみるとほぼ同じ形をしています。
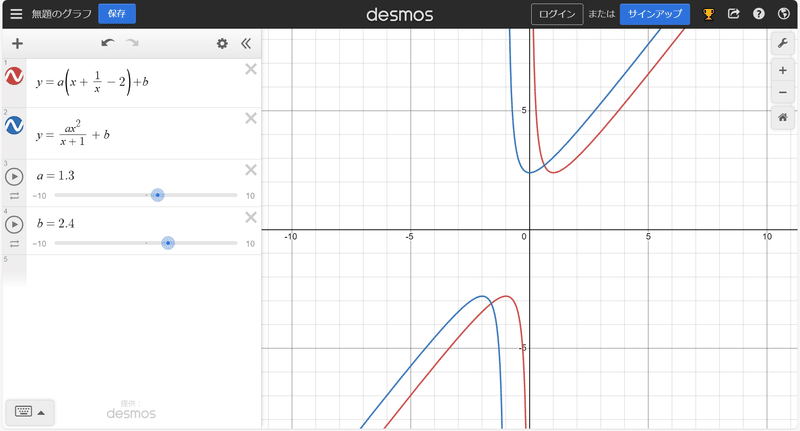
ということは、$${a(z+\frac{1}{z}-2)+b}$$型関数の問題を$${\frac{az^2}{z+1}+b}$$の問題に帰着させ、得られた解を元の問題の解に変換する、という事ができそうです。
$${a(z+\frac{1}{z}-2)+b}$$よりも$${\frac{az^2}{z+1}+b}$$の方が式が短いので、$${a(z+\frac{1}{z}-2)+b}$$という形だと難しい問題でも$${\frac{az^2}{z+1}+b}$$で考えれば難易度が下がるだろう、と考えました。
$${g(z)=\frac{\alpha z^2}{z+1}+\beta}$$、$${h(z)=z-1}$$と置くと$${h^{-1}(g(h(z)))=\alpha (z+\frac{1}{z}-2)+1+\beta}$$となるので、これを$${f(z)}$$とします。
すると$${f(f(f(1)))=0}$$という条件は、
$${f(f(f(1)))\\=h^{-1}(g(h(h^{-1}(g(h(h^{-1}(g(h(1)))))))))\\=h^{-1}(g(g(g(h(1)))))\\=g(g(g(0)))+1=0}$$
・・・という風に書き換えることができます。
このまま$${g(g(g(0)))}$$を計算しようとしてもまだ式が複雑すぎるので、さらにもう一つ小細工をします。
$${\alpha=\frac{(a-b)(b+1)}{b^2}}$$、$${\beta=b}$$とすると、$${g(g(0))}$$は以下のようになります。
$${g(g(0))\\=g(\frac{\alpha×0^2}{0+1}+b)\\=g(b)\\=\frac{(a-b)(b+1)}{b^2}×\frac{b^2}{b+1}+b\\=a-b+b\\=a}$$
このように$${g^2(0)}$$が短い式になるので、$${g(g(g(0)))+1}$$も少しは簡単になりそうです。
実際に計算してみると$${g(g(g(0)))+1=(b+1)(\frac{(a-b)a^2}{b^2(a+1)}+1)}$$になりますが、$${b=-1}$$だと$${\frac{(a-b)(b+1)}{b^2}=0}$$になり最終的に$${f(z)}$$が定数関数になってしまいます。
残りの部分を整理すると$${(a+1)b^2-a^2b+a^3=0}$$という$${b}$$についての2次方程式になり、解の公式を使うと$${b=\frac{a^2\pm\sqrt{-a^3(3a+4)}}{2a+2}}$$になります。
ここで$${a=-d^2}$$と置くと、
$${b=\frac{d^4\pm\sqrt{d^6(-3d^2+4)}}{-2d^2+2}\\=\frac{d^4\pm d^3\sqrt{-3d^2+4}}{-2d^2+2}}$$
・・・と変形でき、あとは$${-3d^2+4}$$が何らかの有理式の2乗になれば$${a,b}$$を両方とも有理式で表せそうです。
最初の方で紹介した3次関数の記事でも同じ状況に何度も遭遇しており、対処法はそちらで紹介済みなので説明は省略します。
結果的に$${d=-\frac{4c}{c^2+3}}$$と置くことで$${-3d^2+4=(cd+2)^2}$$となり、$${a}$$と$${b}$$を$${c}$$の有理式で表す準備が整いました。
まとめると、
$${g(z)=\frac{\alpha z^2}{z+1}+\beta}$$
$${h(z)=z-1}$$
$${f(z)=h^{-1}(g(h(z)))=\alpha(z+\frac{1}{z}-2)+1+\beta}$$
$${\alpha=\frac{(a-b)(b+1)}{b^2}}$$
$${\beta=b}$$
$${b=\frac{a^2\pm\sqrt{-a^3(3a+4)}}{2a+2}}$$
$${a=-d^2}$$
$${d=-\frac{4c}{c^2+3}}$$
・・・となり、$${b}$$の符号で+を選んでひたすら代入と整理を行うと$${f(z)=-(\frac{c^4}{256}-\frac{c^2}{64}+\frac{c}{4}+\frac{43}{128}-\frac{192c^3+36c^2-81}{256c^4})(z+\frac{1}{z}-2)+1+\frac{64c^3}{c^6-2c^5+3c^4-12c^3-9c^2-81c-27}}$$という解が得られます。
ちなみに符号選択で-を選んだ場合は$${f(z)=-(\frac{c^4}{256}-\frac{c^2}{64}-\frac{c}{4}+\frac{43}{128}+\frac{192c^3-36c^2+81}{256c^4})(z+\frac{1}{z}-2)+1-\frac{64c^3}{c^6+2c^5+3c^4+12c^3-9c^2+81c-27}}$$という解になるのですが、実はこれはプラスの方の解の$${c}$$を$${-c}$$に置き換えただけの解です。

マンデルブロ集合は180度回転した見た目になり、ジュリア集合もプラスの方と同じ見た目のものしか存在しないようです。
