
コラッツフラクタルって20種類(以上)あんねん
コラッツ予想:
任意の自然数$${a_0}$$について、$${a_m=1}$$となるような自然数$${m}$$が存在するだろう。ただし、$${a_n}$$の定義は以下の通り。
$${a_{n+1}=\begin{cases}\frac{a_n}{2}&\text{if} a_nが偶数\\3a_n+1&\text{if} a_nが奇数\end{cases}}$$
どうも、解く気もないのに常にコラッツ予想のことが気になっている108Hassiumです。
2021年に1億2千万円の賞金が懸けられたことが報じられて以来、コラッツ予想という単語を知る人は大分増えたと思いますが、そういう人でも「コラッツフラクタル」というものはあまり知らないのではないでしょうか。
wikipediaの「コラッツの問題」のページには、以下のような画像があります。

英語版の記事をよく読むと、この図形がコラッツフラクタルと呼ばれているという記述があります。
しかし、私はこう思うのです。
「これ以外のフラクタル図形が『コラッツフラクタル』と呼ばれてもいいのでは?」
後で紹介する定義を読むとわかる(かもしれない)と思うのですが、あの図形はコラッツ予想という存在に対して唯一無二のものでもなんでもなく、数ある「コラッツ予想と関連するフラクタル図形」の内の一つに過ぎないのです。
ということは、コラッツ予想と関係のあるあらゆるフラクタル図形は、アレ以外のものでもコラッツフラクタルと呼ばれる権利があるのではないでしょうか。
というわけで、コラッツ予想と関係あるフラクタルをいくつか集めてみたので紹介したいと思います。
cos系
まず、先程のフラクタル図形の定義を説明します。
コラッツ予想は、以下のように少しだけ書き換えることができます。
コラッツ予想(ショートカット版):
任意の自然数$${b_0}$$について、$${b_m=1}$$となるような自然数$${m}$$が存在するだろう。ただし、$${b_n}$$の定義は以下の通り。
$${b_{n+1}=\begin{cases}\frac{b_n}{2}&\text{if} b_nが偶数\\\frac{3b_n+1}{2}&\text{if} b_nが奇数\end{cases}}$$
最初に書いた定義では、$${a_n}$$が奇数のとき$${a_{n+1}}$$は必ず偶数になります。
なので$${a_n}$$が奇数のときは$${a_{n+2}=\frac{3a_{n+1}+1}{2}}$$であることが確定するので、この部分の計算を1項分にまとめたのが$${b_n}$$です。
さて、ここからさらに以下のように変形することもできます。
コラッツ予想(ショートカット版):
任意の自然数$${c_0}$$について、$${c_m=1}$$となるような自然数$${m}$$が存在するだろう。ただし、$${c_n}$$の定義は以下の通り。
$${c_{n+1}=\frac{c_n}{2}×\frac{1-\text{cos}(\pi c_n)}{2}+\frac{3c_n+1}{2}×\frac{1+\text{cos}(\pi c_n)}{2}}$$
$${\frac{1-\text{cos}(\pi x)}{2}}$$という関数は、$${x}$$が偶数のときは0、奇数のときは1になります。
そして、逆に$${\frac{1+\text{cos}(\pi x)}{2}}$$は偶数のときは1、奇数のときは0になります。
この性質により、$${\frac{c_n}{2}×\frac{1-\text{cos}(\pi c_n)}{2}+\frac{3c_n+1}{2}×\frac{1+\text{cos}(\pi c_n)}{2}}$$は、$${c_n}$$が偶数なら$${\frac{c_n}{2}}$$に、奇数なら$${\frac{3c_n+1}{2}}$$になり、$${b_n}$$の定義と一致することがわかります。
さて、どうやら先程紹介した元祖・コラッツフラクタルは、初期値を複素数に拡張して$${c_n}$$を計算し、$${c_n}$$が無限大に発散するスピードに応じて複素数を色分けしたもののようです。($${c_n}$$の定義式はwikipediaに書いてあるものとは見た目が異なりますが、実質的には全く同じです)

このフラクタル図形は、「ジュリア集合」と呼ばれるグループに属するものです。
ジュリア集合とは、ある複素関数$${f(z)}$$を使って$${z_{n+1}=f(z_n)}$$と表せる数列が無限大に発散しない初期値の集合(本来の定義とは異なるのですが、面倒なのでこの記事ではこの説明で通します)として定義されるフラクタル図形です。
これと対を成すものとしてマンデルブロ集合というグループがあり、ある2変数複素関数$${f(z,c)}$$を使って$${z_{n+1}=f(z_n,c)}$$と表せる数列が無限大に発散しない定数$${c}$$の集合と定義されます。(本来は$${f(z,c)=z^2+c}$$かつ$${z_0=0}$$であるもののみを指す名称らしいですが、不便なのでこの記事ではより広い単語として扱います)
さて、コラッツ予想には以下のような形の派生問題が存在します。
コラッツ予想派生問題(ショートカット版):
奇数$${k}$$と初期値$${d_0}$$に対して以下の数列$${d_n}$$はどんな性質を持つか?
$${d_{n+1}=\begin{cases}\frac{d_n}{2}&\text{if} d_nが偶数\\\frac{3d_n+k}{2}&\text{if} d_nが奇数\end{cases}}$$
$${k=1}$$のときが本来のコラッツ予想のショートカット版で、例えば$${k=5}$$に変えると1に到達する初期値としない初期値に分かれるといった変化が起きます。
というわけで、$${k}$$を二つ目の変数と見做してマンデルブロ集合を描画してみました。


※マンデルブロ集合の見た目は初期値によって変わります。本来は「標準の初期値」みたいな感じのものが存在するのですが、正確な値は計算できませんでした。
$${k}$$を適当な値に固定することで、先程のものとは違うジュリア集合を無限に得ることができます。
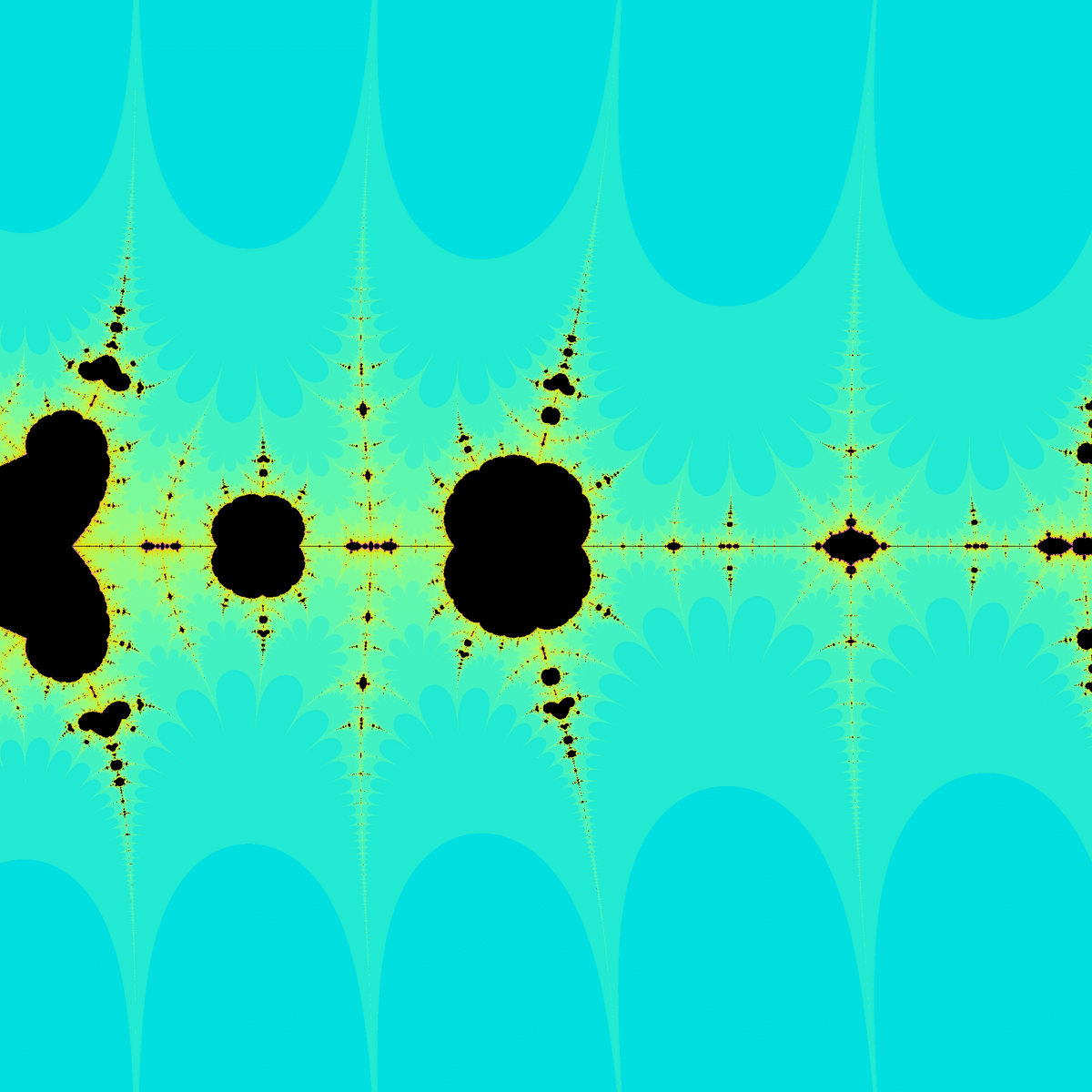



後半の二枚についてはもはやコラッツ予想派生問題とは対応していませんが、それでも元をたどればコラッツ予想に行きつくのでコラッツ予想とは無関係ではない(≒コラッツフラクタルと呼ばれてもいい)と思います。
コラッツ予想派生問題には、以下のようなものもあります。
コラッツ予想派生問題2(ショートカット版):
奇数$${k}$$と初期値$${e_0}$$に対して以下の数列$${e_n}$$はどんな性質を持つか?$${e_{n+1}=\begin{cases}-\frac{e_n}{2}&\text{if} e_nが偶数\\\frac{3e_n+k}{2}&\text{if} e_nが奇数\end{cases}}$$
これを基にしたフラクタル図形は以下のようになります。



さて、ここまでのものは全てショートカット版をもとにしていましたが、ショートカット無しバージョンを使って同じことをするとこうなりました。
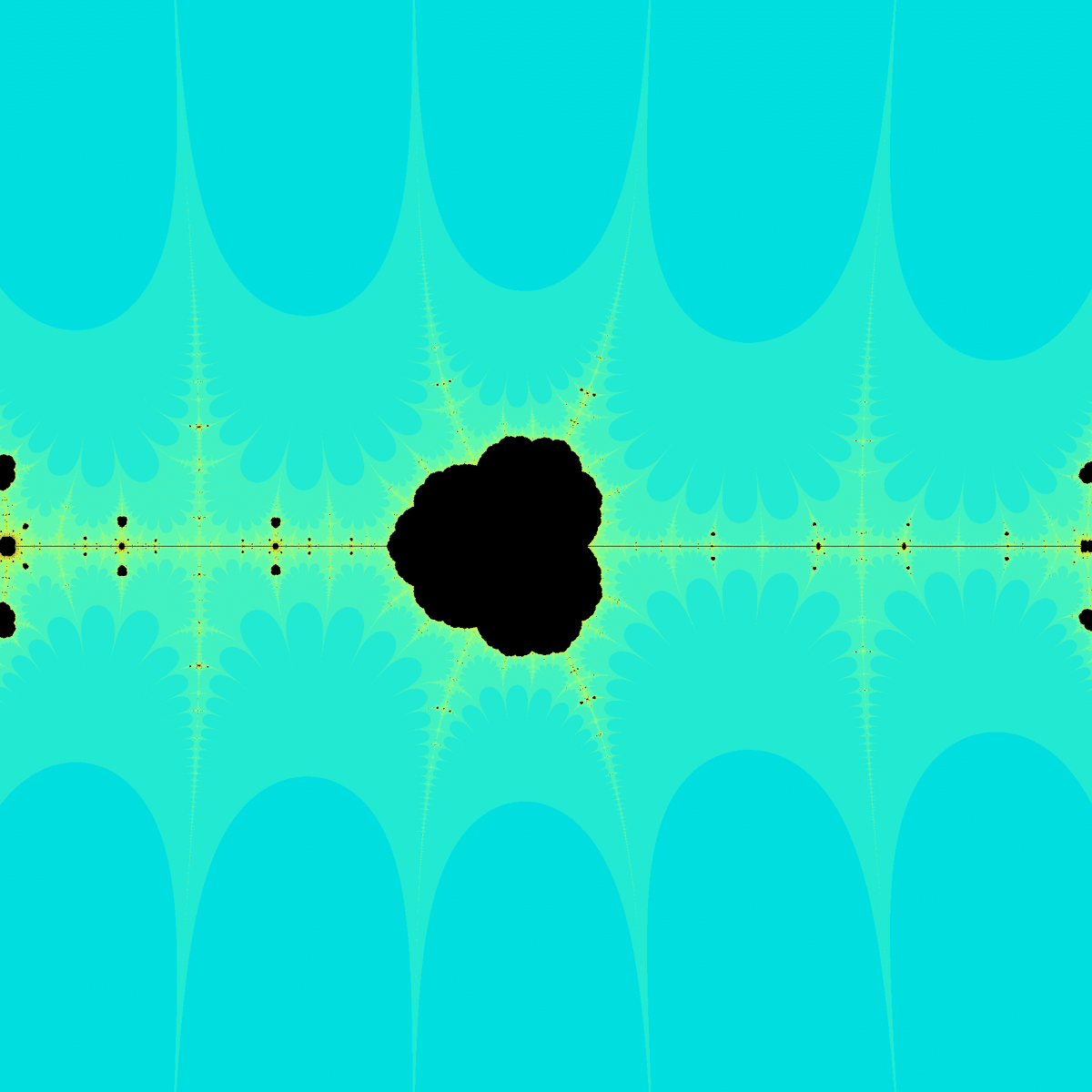


これとは逆に、ショートカットの回数を増やすこともできます。
コラッツ予想(mod 4版):
任意の自然数$${f_0}$$について、$${f_m=1}$$となるような自然数$${m}$$が存在するだろう。ただし、$${f_n}$$の定義は以下の通り。
$${f_{n+1}=\begin{cases}\frac{f_n}{4}&\text{if} f_n\equiv0\pmod4\\\frac{3f_n+1}{4}&\text{if} f_n\equiv1\pmod4\\\frac{3f_n+2}{4}&\text{if} f_n\equiv2\pmod4\\\frac{9f_n+5}{4}&\text{if} f_n\equiv3\pmod4\end{cases}}$$
※「$${a\equiv b\pmod n}$$」は「$${a}$$を$${n}$$で割った余りは$${b}$$を$${n}$$で割った余りと等しい」という意味の式です。
試行錯誤の結果、この数列は以下のように変形できることがわかりました。
コラッツ予想(mod 4版):
任意の自然数$${g_0}$$について、$${g_m=1}$$となるような自然数$${m}$$が存在するだろう。ただし、$${g_n}$$の定義は以下の通り。
$${g_{n+1}=\frac{g_n(\text{cos}(\pi g_n)+1)(\text{cos}(\frac{\pi}{2}g_n)+1)}{16}+\frac{(3g_n+1)(\text{cos}(\pi(g_n-1))+1)(\text{cos}(\frac{\pi}{2}(g_n-1))+1)}{16}+\frac{(3g_n+2)(\text{cos}(\pi(g_n-2))+1)(\text{cos}(\frac{\pi}{2}(g_n-2))+1)}{16}+\frac{(9g_n+5)(\text{cos}(\pi(g_n-3))+1)(\text{cos}(\frac{\pi}{2}(g_n-3))+1)}{16}}$$



exp系
ここまでは2で割った余りによる場合分けを表現するのにコサインを使っていましたが、他のやり方もあります。
まず$${(-1)^n}$$は$${n}$$が偶数のときは1、奇数のときは-1になります。
これを利用すると、$${n}$$を2で割った余りは$${\frac{1-(-1)^n}{2}}$$と表すことができます。
さらに、オイラーの等式から$${-1=e^{i\pi}}$$と表せることがわかるので、$${n}$$を2で割った余りは$${\frac{1-e^{i\pi n}}{2}}$$と変形できます。
以上を踏まえると、コラッツ予想は以下のように書き換えることができます。
コラッツ予想(ショートカット版):任意の自然数$${h_0}$$について、$${h_m=1}$$となるような自然数$${m}$$が存在するだろう。ただし、$${h_n}$$の定義は以下の通り。
$${h_{n+1}=\frac{h_n(1-e^{i\pi h_n})}{4}+\frac{(3h_n+1)(1+e^{i\pi h_n})}{4}}$$
これを複素数に拡張することで、全く新しいフラクタル図形が生まれます。



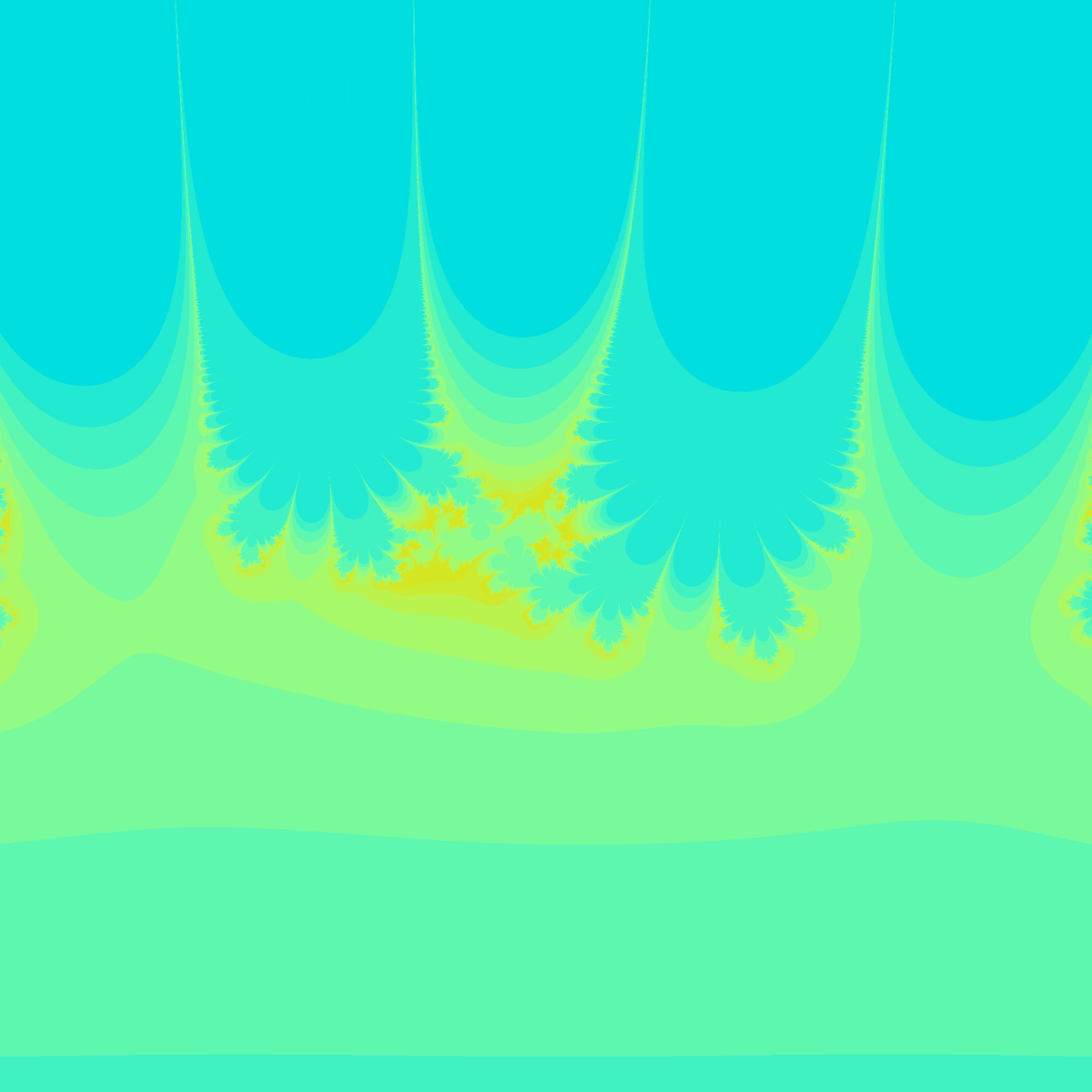


mod系
初等関数(多項式、三角関数、指数関数等)の組み合わせで表せることに拘らなければ、もっと簡単にコラッツ数列を複素数に拡張することができます。
まず、実数$${x}$$と自然数$${n}$$に対して$${\text{mod}(x,n)}$$を「$${x}$$の整数部分を$${n}$$で割った余りと$${x}$$の小数部分の和」と定義します。

そして、$${z=x+iy}$$に対して$${\text{mod}(x,2)+iy}$$を$${\frac{1-\text{cos}(\pi z)}{2}}$$や$${\frac{1-e^{i\pi z}}{2}}$$の代わりに使うことで、今までと同様にフラクタル図形を生み出すことができます。



$${\text{mod}(x,2)+i\text{mod}(y,2)}$$という関数も、2で割った余りの拡張としては自然な気がします。


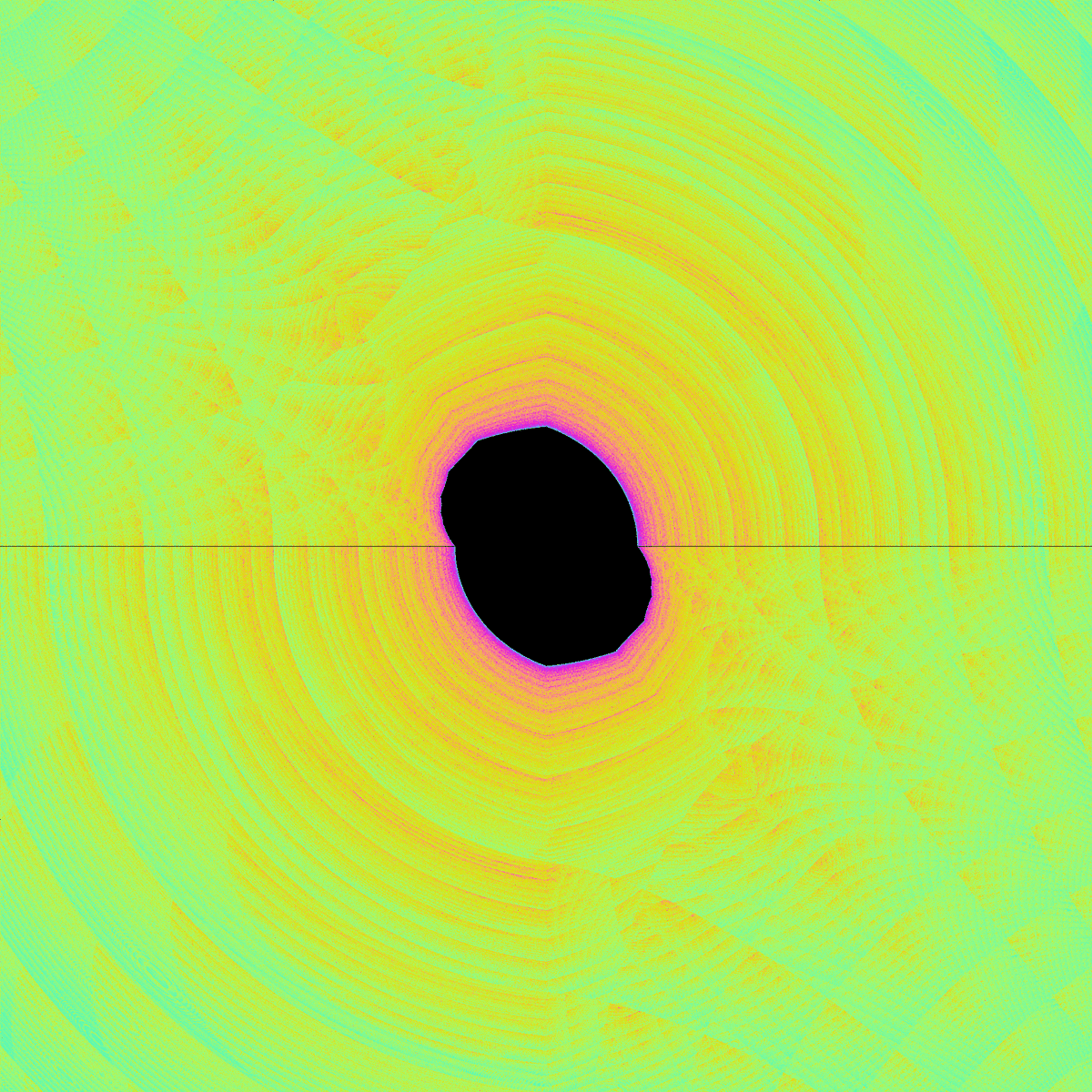
ところで、ここまでの画像はProcessingというプログラミング言語を使って作成したものですが、この言語には割り算の余りを表す"%"という演算子があります。
$${x\%2}$$は意味的には$${\text{mod}(x,2)}$$と同じになりそうですが、実は$${x}$$が負のときの仕様が異なります。

これを$${\text{mod}(x,2)}$$の代わりに使うと、先程のものとは異なるフラクタル図形になります。






その他
整数を(実数を経由せずに)複素数に拡張した概念として、「ガウス整数」というものがあります。
ガウス整数は実部と虚部がともに整数であるような複素数のことで、以下のようにガウス整数上でもコラッツ予想の派生問題を考えることができます。
コラッツ予想派生問題(ガウス整数版):
初期値$${j_0}$$に対して以下の数列$${j_n}$$はどんな性質を持つか?
$${j_{n+1}=\begin{cases}\frac{j_n}{2}&\text{if} j_n\equiv0&\pmod2\\3j_n+1&\text{if} j_n\equiv1&\pmod2\\3j_n+i&\text{if} j_n\equiv i&\pmod2\\\frac{j_n+1+i}{2}&\text{if} j_n\equiv1+i&\pmod2\end{cases}}$$
この数列が発散する(ように見える)初期値を発散速度に応じて色分けすると、以下のようになります。

何やらカラフルな模様が現れました。
他の数列だとこんな感じです。

※キャプションに書いてあるのは数列の定義の略記です。説明は省くので気になる人は気合で解読してください。

これらはあまりフラクタル図形っぽく無いですが、稀にフラクタル図形っぽくなることもあります。

拡大してみると鎖状の模様が所々に見えますが、その周りをよく見ると繰り返し構造になっていることがわかります。


これらは「シェルピンスキーのギャスケット」という有名なフラクタル図形に似ている部分が見られます。
おまけ(ギャラリー)
記事内で使った画像(の一部)の横長バージョンです。

























解説の面倒臭さに対して面白さが割に合わないと思って没にしたものです。




