
セル・オートマトンと謎の数列
この記事は日曜数学 Advent Calendar 2022 - Adventarの参加記事です。
どうも、108Hassiumです。
色々なルールのセル・オートマトンで遊んでいると、以下のような謎の数列とよく遭遇します。
1, 2, 1, 6, 4, 14, 1, 14, 12, 62, 8, 126, 28, 30, 1, 30, 28, 1022, 24, 126, 124, 4094,…
この数列は、振動物体の周期として現れます。
例として、B7/S12345というルールを考えます。
「B7/S12345」という文字列はBの後が誕生条件、Sの後が生存条件を表しており、
死んだセルが7個の生きたセルと接していたら生きたセルに変わる
生きたセルが1~5個の生きたセルと接していたら生き残り、そうでなければ死んだセルに変わる
というルールであることを表しています。
このルールで、以下のような形の物体を考えます。
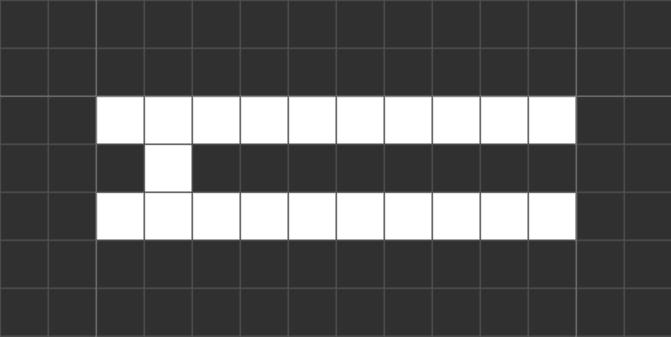
1行目と3行目に生きたセルを隙間無く並べ、2行目は2列目にだけ生きたセルを置いたパターンです。
B7/S12345では、このようなパターンは振動物体になります。

先程の横幅が10セルの例だと、14周期の振動物体になります。
そして、横幅を1セルずつ増やしたものの周期を調べていくと、冒頭の数列が現れるのです。

なお、全てのパターンが初期状態(2行目の生きたセルが左から2番目の位置にしかない状態)に戻ってくるわけではなく、初期状態を含まないループに入ったり可動部が死滅したりすることがあります。
上の画像は説明通りの初期状態ではなく最終的に到達する振動物体を表しているので、2行目のセルの位置がずれていたり無くなってたりします。(固定物体は1周期の振動物体とみなせるので、可動部が消えるパターンは1周期として記載してあります)
数列の項をよく見てみると、以下のような性質がありそうに見えます。
予想1:$${a_{2^k-1}=1}$$
予想2:どの項も2の冪乗の差として表せる
初項を$${a_1}$$とすると$${a_n=1}$$を満たすのは$${n=1,3,7,15}$$で、確かにどれも$${2^k-1}$$と表せる数です。
この性質に関しては、実際の物体の動きを観察してみると成り立ちそうなのがわかりやすいです。

予想2に関しては、例えば
$${1=2^1-2^0}$$
$${2=2^2-2^1}$$
$${4=2^3-2^2}$$
$${6=2^3-2^1}$$
$${8=2^4-2^3}$$
$${12=2^4-2^2}$$
$${14=2^4-2^1}$$
$${24=2^5-2^3}$$
$${28=2^5-2^2}$$
・・・というように成り立っているように見えますが、こっちは仕組みがよくわかりませんでした。
というわけで、オンライン整数列大辞典OEISの力を借りてみることにしました。
OEISはその名の通りいろいろな整数列が載っている辞典のようなサイトで、数列の項やキーワードを入力すると関連する数列を探してくれます。
というわけで検索してみたところ、それっぽい数列が見つかりました。
どうやらA268754は「B1/Sのn×1の長方形の振動物体(左端の1セルだけ生きているのが初期状態)の周期」を表す数列のようです。
定義に使われているルールが違いますが、実際に振動物体を観察してみるとB7/S12345のものと同じ動きをしていることがわかります。

ちなみに、Golly(セル・オートマトンのシミュレーションソフト)ではControl→Set Ruleを選んで"B1/S:P10,1"と入力すると上の振動物体をシミュレートできます。
さて、OEISの"COMMENTS"の項目の2行目以降を翻訳すると以下のようになります。
2^k-1番目の項は、全てのセルが死ぬので1になる。
2進法では、全ての項(1を除く)は1個以上の1の後に1個以上の0が並んだ形をしている。例外は第36項と94項とその派生物で、2進展開すると1と0が交互に並ぶ。
この文章は、先程述べた2つの予想について言及しています。
最初の文は予想1と全く同じことを言っており、「2進法で11..100…0と書ける数」は「2の冪乗の差で表せる数」でもある(逆は成り立たない)ので2文目も予想2の話をしていて、最後の文では例外の存在について述べています。
また、"FORMULA"の項目にはこう書いてあります。
偶数番目の項の一般式は知られていない。奇数番目の項については、a(2n+1)=2*a(n)が成り立つが、a(n)=1となる場合(n=2^k-1と表せる)は例外となる。
本当に「謎の数列」なんですね。
ところで、ここまででB7/S12345とB1/Sという2つの異なるルールが同じ数列に関係していることが分かったわけですが、冒頭で述べた通りあの数列が出てくるルールは他にもたくさんあります。
というわけで、ここからは謎の数列と関係のあるほかのルールを紹介します。
B2a/S0
最初に紹介するのは、B2a/S0です。
このルール表記は"Hensel notetion"というもので、近傍のセル配置に対して以下のように記号を割り当てたものです。

このルールでは、以下のパターンが数列と関係しています。

動かすとこうなります。

ドミノが分裂と消失を繰り返しながら一定の範囲を移動し続けています。
見た目は違いますが、よく見るとB7/S12345やB1/Sのものと同じ動きをしていることがわかります。
ちなみにここからは余談になりますが、誕生条件に2kを追加したB2ak/S0というルールでは以下の物体が興味深い挙動を示します。

少し動かしてみると、以下のようになります。

振動物体の片側のストッパーを消したような形のパターンを無限に生成するようです。
そして、更に世代を進めると、

フラクタル図形(シェルピンスキーのギャスケット)が現れます。
さらに、以下の物体は、


なんかものすごいフラクタル図形になります。
静止画だと凄さが伝わり切らないので、ぜひGollyをダウンロードして実際に動かしてみてください。
HighLife(B36/S23)
HighLifeは、ライフゲームの誕生条件に6を追加したルールです。
普通のライフゲームとほぼほぼ変わらないような挙動を示すルールなのですが、大きく異なる特徴もあります。
特に面白いのが、以下のような小さな自己複製物体が存在する点です。

このように12世代で2個に分裂し、この後も個体数を増減させながら直線状にのびていきます。
この物体を使って、以下のような振動物体をつくることができます。

右下の固定物体を斜めに4セルずつずらしていくことで、1, 48, 1, 144, 96, 336, 1, 336, 288, 1488, 192, 3024, 672, 720, 1, 720, 672, 24528, 576, 3024, 2976, 98256,…という数列が得られます。

この数列は、A268754の1でない項を24倍にしたものになっています。
実際に、世代数が24の倍数のときの状態を観察してみると、A268754の振動物体と同じ動きをしていることがわかります。

ちなみに、「自己複製物体の複製周期が12世代なら、A268754の12倍の数列になるべきでは?」と思った人もいるかと思います。
実際私もそう思っていたのですが、例えば12周期の振動物体を作ろうとするとストッパーの固定物体がうまく機能せず、なんやかんやで24倍の数列しか作れませんでした。

さて、HighLifeやB2a/S0のもののような自己複製物体が存在するルールは他にもたくさんあり、そういったルールでも(ストッパーが見つかれば)A268754の定数倍の数列が得られます。
例えば、B2ce/S1ではHighLifeと同じくA268754の24倍の、1, 48, 1, 144, 96, 336, 1, 336, 288, 1488, 192, 3024, 672, 720, 1, 720, 672, 24528, 576, 3024, 2976, 98256,…という数列が得られます。

ちなみにストッパーの位置をずらすと銃になります。

また、B3ai4a5a6c7c/S3acein4aceknw5ikny6cek78では少なくとも2つの自己複製物体が存在し、それぞれA268754の65倍と74倍の数列が得られます。


ちなみにライフゲームにも自己複製物体は存在しますが、増殖の仕方が違うのでA268754系数列の生成には使えないようです。
ライフゲーム(B3/S23)
一応、ライフゲームでもA268754と関連する数列を生成する方法があります。
Gollyのルール欄で"B3/S2:T0,3"と入力すると、以下のような画面になります。

グリッドの横幅は無限のままですが、縦幅が3セルになりました。
この状態で以下のようなパターンを作ります。

すると、28周期の振動物体になります。

右側のブロックを1セルずつずらした場合の周期は、以下のようになります。
1, 1, 4, 4, 1, 1, 12, 12, 8, 8, 28, 28, 1, 1, 28, 28, 24, 24, 124, 124, 16, 16, 252, 252, 56, 56, 60, 60, 1, 1, 60, 60, 56, 56, 2044, 2044, 48, 48, 252, 252, 124, 124, 8188, 8188,…
A268754の1でない項を2倍して、全ての項を2個ずつ並べた数列になっています。
グリッドの制限なしでこれと全く同じ数列を生成するルールとして、B7/S123456があります。

B7/S12345と似たような筒状の振動物体ですが、生存条件に6が追加されているので違う動きをします。
ちなみに、初期状態の筒の中のセルを一つ左にずらすと、全く違う動きになります。

左端のセルがずっと生き残り、右方向へ信号を発し続けるようになりました。
この初期状態から生成される数列は、以下のようになります。
1, 2, 1, 4, 6, 6, 12, 12, 8, 8, 20, 20, 14, 14, 12, 12, 38, 38, 16, 16, 34, 34, 12, 12, 12, 12, 36, 36, 62, 62, 60, 60, 56, 56, 96, 96, 208, 208,…
同じ項が2個並ぶ法則が最初だけ崩れていたり、1022のような大きい数が出てこず増減が緩やかだったり、38や34のような見慣れない数が出てきてたりと、いろいろと奇妙な性質を持っているようです。
38と34といえば、ライフゲームにおいて38周期と34周期の振動物体は2022年になって初めて発見されたようです。
ということは、多分B7/S123456の筒状振動物体をライフゲーム上で再現する方法はまだ見つかっていないor調べられていないんでしょうね。
B7/S12345
B7/S123456では筒の端をふさぐと違う数列が得られましたが、一番最初に紹介したB7/S12345でも同じ現象が起きます。
例えば、横幅10セルの振動物体の周期は、最初に紹介したものでは14でした。

しかし、初期状態を変えると以下のように27周期の振動物体になります。

対応する数列は以下の通りです。
2, 3, 2, 5, 8, 13, 2, 27, 12, 37, 16, 32, 28, 2, 2, 29, 56, 24, 24, 24, 188, 124, 56, 32, 301, 252, 219, 56, 102...
最初の方の項からはフィボナッチ数列の香りがしますが、どうやらあまり関係はなさそうです。
両端をふさいだものからは、以下の数列が生成されます。
2, 2, 3, 3, 2, 2, 5, 5, 8, 8, 13, 13, 2, 2, 27, 27, 12, 12, 37, 37, 16, 16, 32, 32, 28, 28, 2, 2, 2, 2, 29, 29, 56, 56, 24, 24, 24, 24, 24, 24, 188, 188, 124, 124, 56, 56, 32, 32, 301, 301, 252, 252, 219, 219, 56, 56, 102, 102...
片側をふさいだものの数列の項を2個ずつ並べた数列になりました。
B7/S123456で同じことをすると、以下の数列が生成されました。
1, 2, 2, 3, 1, 4, 4, 10, 6, 6, 6, 7, 12, 12, 12, 16, 8, 8, 8, 36, 20, 20, 20, 63, 14, 14, 14, 27, 12, 12, 12, 225, 38, 38, 38, 24, 16, 16, 16, 92, 34, 34, 34, 34,…
途中からは同じ項が3つ並んで1個だけ違う項が入る、という構造になっているようです。
片側だけふさいだ場合の数列と比べてみましょう。
片側ふさぎ:1, 2, 1, 4, 6, 6, 12, 12, 8, 8, 20, 20, 14, 14, 12, 12, 38, 38, 16, 16, 34, 34, 12, 12, 12, 12, 36, 36, 62, 62, 60, 60, 56, 56, 96, 96, 208, 208,…
両側ふさぎ:1, 2, 2, 3, 1, 4, 4, 10, 6, 6, 6, 7, 12, 12, 12, 16, 8, 8, 8, 36, 20, 20, 20, 63, 14, 14, 14, 27, 12, 12, 12, 225, 38, 38, 38, 24, 16, 16, 16, 92, 34, 34, 34, 34,…
「片側ふさぎの数列の奇数番目」と「両側ふさぎ数列の4n+1番目(3個連続で出てくる値)」を抽出してみます。
片側:1, 1, 6, 12, 8, 20, 14, 12, 38, 16, 34, 12, 12, 36, 62, 60, 56, 96, 208,…
両側:1, 1, 6, 12, 8, 20, 14, 12, 38, 16, 34,…
同じ数列になりました。
筒状の振動物体群をもつルールは他にもあるので、同様に初期状態の違いによる数列の違いを調べてみました。
B7/S123457


通常の初期状態(左端から2セル目だけ生きている状態)から生成される数列はA268754と全く同じですが、片側/両側ふさぎの初期状態だと違う数列が生成されています。
A268754と共通する項が多そうなので、違う値の部分だけ注目してみます。

まず片側ふさぎの数列は、A268754の3n+2番目だけを2倍にした数列になっているようです。
両側ふさぎの方は少し不規則に見えますが、おそらく「A268754の3n+2番目以外かつ1でない項を1/2倍にした数列」になっていると思われます。
今まではA268754の整数倍の数列や2項ごと・4項ごとに区切ると規則性があるような数列が出てきましたが、「0.5倍」と「3項ごと」が絡んでくるのは予想外でした。
B7/S123458

先程のB7/S123457と同様に、通常の初期状態からはA268754が、それ以外は謎の数列になっています。
まず片側ふさぎの数列ですが、19と17という数字を見てピンと来たので調べてみたところ、B7/S123456(ライフゲームの再現)の片側ふさぎ数列と似ていることを発見しました。

B7/S123456の方の数列の奇数番目と2番目の項を消去すると、なんとB7/S123458の数列を2倍した数列になるのです。

この関係は、B7/S123456の通常数列とA268754の関係とほぼ同じです。
では両側ふさぎの方は何なのかというと、B7/S123456の片側ふさぎ数列の初項を消したものの1/2倍と途中から一致します。

どうもB7/S123456の片側ふさぎ数列の最初の方の項は不規則らしく、何かと例外にされがちですね。
ちなみにこれは完全に余談になってしまいますが、19といえば2022年12月2日現在ライフゲームにおいて19周期の振動物体は見つかっていないらしく、「ライフゲームは任意の自然数nに対してn周期の振動物体を持つか?」という問題は未解決だそうです。(n≥43の任意の周期の振動物体を作る方法が見つかっており、19周期と41周期が見つかれば完全解決されるらしいです)
また、以下のページではこの記事で扱っているような振動物体を基にして任意の周期を持つ振動物体を作り出せるかについて議論しているようです。(正確な内容は英語なのでよくわかりませんでした)
B7/S1234568

通常数列と片側ふさぎ数列はパッと見A268754と同じように見えますが、並べてみると微妙に違います。

値の変わっている位置も等間隔ではないし、ズレ方もバラバラ、そして通常数列と片側ふさぎ数列の値もちょっとだけ違います。
とりあえず分かったのは、2^m-1番目の項(A268754では全部1)が2^mに変わるっぽいことです。(上の表の範囲外でも成り立っているようでした)
両側ふさぎ数列の方はというと、最初の2項以外は片側ふさぎ数列の1/2倍というシンプルな法則のようです。
ルール18
これまで紹介したルールは、実は1次元セル・オートマトンと関係があります。
1次元セル・オートマトンと聞くとフラクタル図形を思い浮かべる人が多いと思いますが、あれは縦軸を時間軸として各世代のセルの配列を順番に並べた際にできる図形で、1次元セルオートマトンの実体は名前の通り1次元のセルの列です。

Gollyでは、ルール欄に"W18"と入力するとルール18をシミュレートできます。
ルール18は、以下のようなルールです。

実はこのルール、B7/S12345の筒状振動物体の動作規則と一致しています。

また、B7/S12345がルール18と関係しているなら当然B2a/S0とB2ak/S0もルール18に対して同様な関係があり、B2ak/S0のフラクタル図形を描くパターンの挙動も「ルール18だから」で大まかには説明できます。
ちなみに、HighLifeとB2ce/S1にも「自己複製物体を平行に並べ続けるパターン」が存在し、ルール18と同様にシェルピンスキーのギャスケットを生成します。
話は少し戻りますが、筒状振動物体のあるB7/S12345以外のルールも、1次元セル・オートマトンと対応付けることができます。
まず、B7/S123456(ライフゲームの再現)はルール22と同じ動きです。

そして、B7/S123457はルール90、B7/S123458はルール146に対応しているようです。
なおルール18、22、90、146は1セルの初期状態から始めるとシェルピンスキーのギャスケットが生成されるという共通点がありますが、そうではないルールの例としてルール150があります。
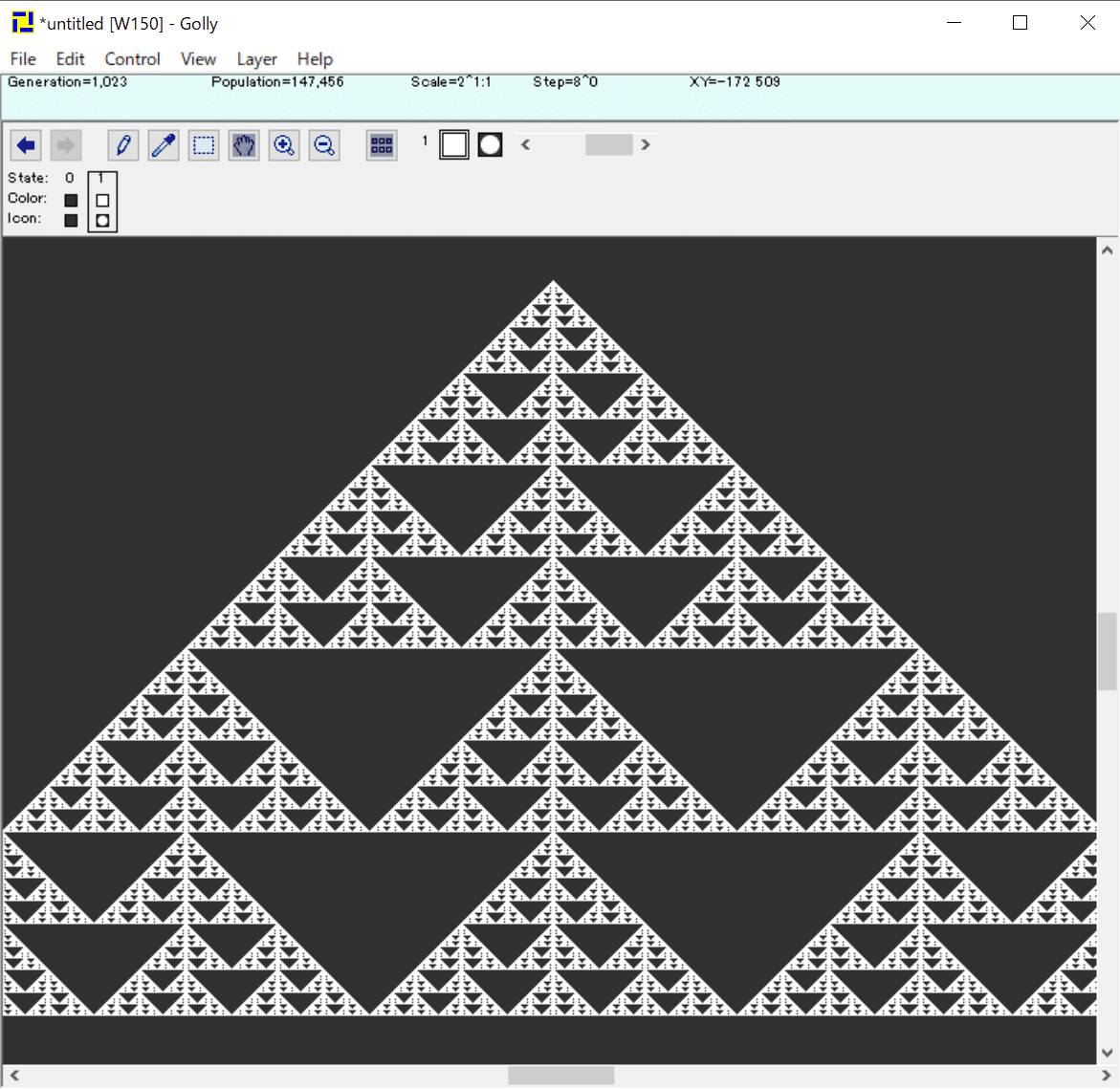
そんなルール150ですが、B7/S1234568の筒状振動物体で再現できます。

ところでGollyでは"W"+数字をルール欄に入力すれば1次元セル・オートマトンをシミュレートできるのですが、数字の部分が奇数のルールには対応していないようです。


そんな奇数ルールも、実は筒状振動物体で再現できます。
例えばルール73は、B6/S123457で再現できます。


誕生条件に7ではなく6を使っているので、奇数ルール特有の「何もない空間にセルが生まれる」という挙動を再現できています。
なお、筒状振動物体で全ての基礎セル・オートマトン(3近傍1状態1次元セル・オートマトンのこと)を簡単に再現できるわけではなく、例えばチューリング完全性で有名なルール110はルール自体が左右非対称な性質を持っているためこれまでのやり方では再現できないっぽいです。
2×2(B36/S125)
A268754が現れるルールとして、2×2(B36/S125)というものがあります。
このルールで数列を生成する振動物体群は今までのものとは大きく異なり、棒状の初期状態から正方形を描くように伸縮します。

2×2nの長方形は同様の振動物体になり、その周期はA268754と一致します。
ちなみに、OEISには2×4nの長方形を初期状態としたときの周期の列がA160657として登録されているようです。
また、A268754のページには「偶数番目の項はA160657と一致する」とも書いてあります。
さて、B36/S125の振動物体群は、似た形の亜種のようなものがいくつか存在します。
例えば既に紹介したB2ce/S1(自己複製物体があるルール)では、以下のような振動物体も存在します。

B36/S125と同じように、「1セルの間隔をあけてn個のセルを一直線に並べた初期状態から生成される振動物体の周期」はA268754と一致します。
なのでB2ce/S1というルールは、A268754と関連する全く異なる2つの振動物体群を持っている珍しい(多分)ルールなのです。
B2c3i4i/Sでは、間の空いていない一直線の初期状態が振動物体になります。

初期状態の幅が奇数だと上手く振動物体にならずに崩壊してしまうことが多いですが、B2c3-cekq4ikt5i8/S2-in3-acky4aijry5eiky6iというルールでは奇数幅でも安定します。

B2c3-cekq4ikt5i8/S2-in3-acky4aijry5eiky6iの1×nの初期状態から生成される数列は、OEISでA298819として登録されています。
B3i6i/S2i5i8では、同じ一直線の初期状態でもB2c3i4i/Sとは違った動きをします。

また、このルールではB2c3-cekq4ikt5i8/S2-in3-acky4aijry5eiky6iとは異なり幅2n-1の初期状態と2nの初期状態からは同じ周期の振動物体ができるようなので、「n個のセルを一直線に並べた初期状態から生成される振動物体の周期」はA268754の項を2個ずつ並べた数列になります。
B2c3c/S2c3cでは、「2×nの長方形の中に上下に交互にセルを並べた初期状態」からA298819と同じ数列が生成されます。(ただしA298819では全てのセルが死んだ場合の項は1ではなく0と定義されています)


B2e/Sでは、B36/S125の振動物体を45度回転させたような形の振動物体群が存在します。

余談ですが、同じ振動物体が存在するB2ae/Sというルールで以下のパターンを動かしてみると、

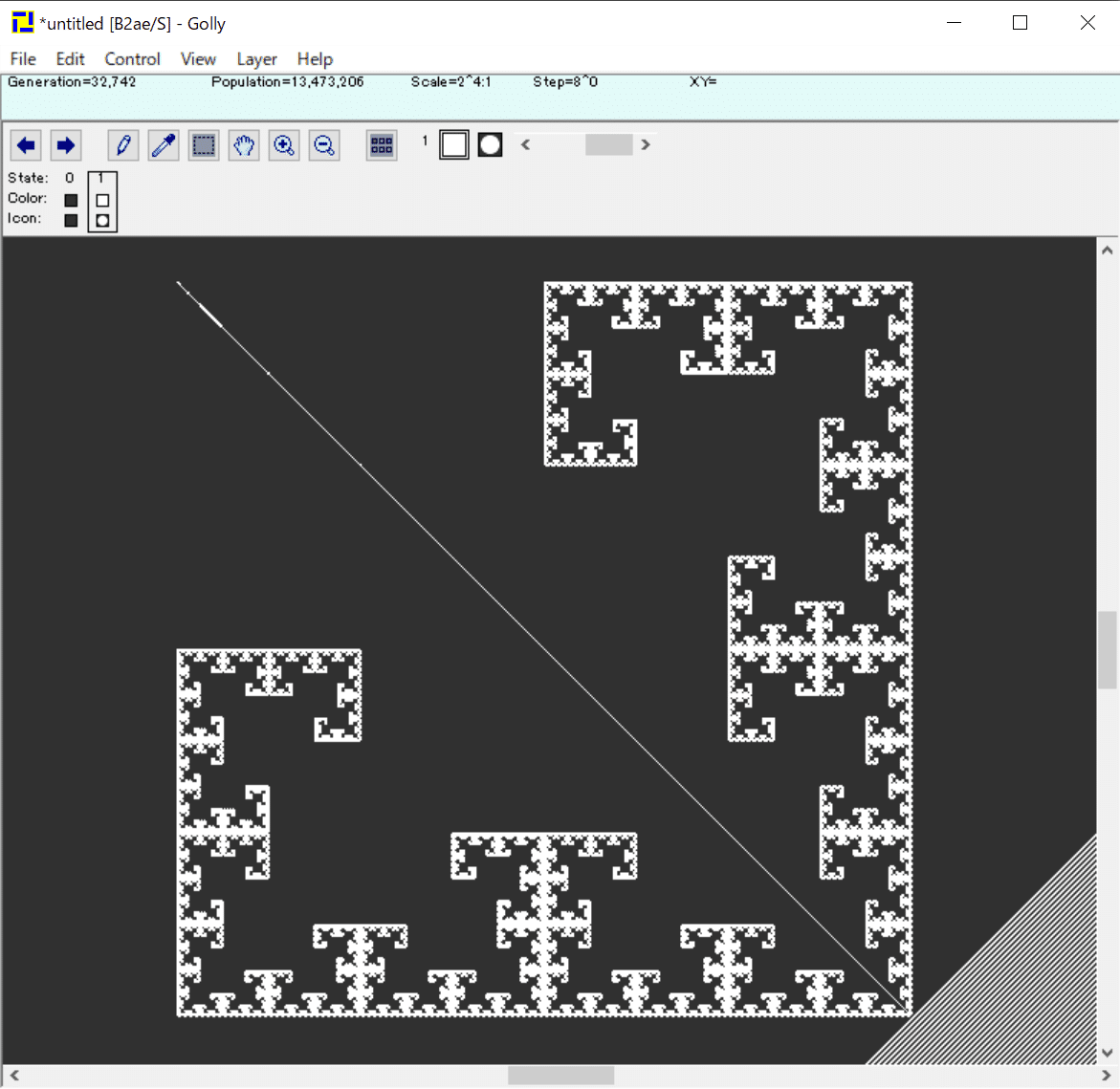
"T-square"というフラクタル図形が出現します。
シェルピンスキーのギャスケットに関しては基礎セル・オートマトンを介して振動物体との繋がりがなんとなく説明できましたが、T-squareに関してはよくわかりません。
B2en3ai/S01c5iでは、B36/S125と同じ振動物体と45度回転させた形の振動物体が両方存在します。

なお45度回転の方は、先程のB2e/Sのものとは違う挙動になっています。
その他
他のものとの関連付けがしにくいものをまとめて紹介します。
B2ck/S3a4q

ジグザグに並んだブロックのカドをセルが移動していくような振動物体群のあるルールです。
左下のブロックの左上だけに可動部がある状態を初期状態とすると、以下の数列が生成されます。
2,6,14,14,62,126,30,30,1022,126,4094,2046,1022,32766,62,62,8190,524286…
この数列はA268754の偶数番目と等しいです。
振動物体をよく観察してみるとB7/S12345の筒状振動物体と実質的に同じ動きをしており、なおかつブロックを一つ増やすと可動部の可動範囲が2セルずつ増えるため、A268754の偶数番目になるのはほぼ自明と言えます。

同様な性質の振動物体群を持つルールとして、B2ek3j5y/S1eがあります。

B2a3i4i/S2c

B2a/S0と似ていますが、自己複製物体がぶつかると間に生きたセルが2つ生まれ、それによって複製が阻害されるため異なった動きになっているようです。
数列はこうなりました。
2, 1, 1, 8, 6, 6, 1, 1, 1, 20, 18, 18, 12, 12, 12, 44, 42, 42, 1, 1, 1, 44, 42, 42, 36, 36, 36, 188, 186, 186, 24, 24, 24, 380, 378, 378, 84, 84, 84, 92, 90, 90, 1, 1, 1, 92, 90, 90, 84, 84, 84, 3076, 3066, 3066, 72, 72, 72, 380, 378, 378…
やたらと同じ項がたくさんあります。
6項ずつ区切ると法則性が見えてきそうだったので、区切ってみました。

とりあえず、
a(6n+1)=a(6n+2)=a(6n+3) (n>0)
a(6n+5)=a(6n+6)
が成り立ちそうです。
また、a(6n+4)=a(6n+5)+2が成り立ちそうだと思いきや、n=8で急に崩れます。
そして、a(6n+2)とa(6n+3)はA268754の奇数番目の項の1以外の値を3倍にした数列で、a(6n+5)とa(6n+6)は偶数番目の3倍になっているようです。
しかし、残ったa(6n+4)については、全て4の倍数という共通点はあるものの既存の数列との関連性は見つけられませんでした。
さて、こんな感じの訳分からない数列ですが、なんと別のルールでも出現を確認しました。

筒状振動物体の片側の壁を取り払ったような見た目ですが、残った壁も時々穴が開いてその度に可動部の動きを阻害します。
どうやら壁の穴がB2a3i4i/S2cの自己複製物体の間に生まれるセルと同じ役割を果たすようで、B2a3i4i/S2cと全く同じ数列が生成されます。
B1e2e/S2ei3r

左の振動物体はB2e/Sの正方形の振動物体と同じ動きで、右側は筒状振動物体を45度傾けたような動きになっていることがわかります。
この2つの振動物体は、実は以下のような同一の初期状態から生成されています。

この初期条件から、以下の数列が生成されます。
1, 2, 4, 6, 12, 4, 28, 14, 28, 4, 124, 156, 252, 14, 60, 30, 60, 28, 2044, 126, 252, 28…
まず、この数列の2n+1(n>0)番目の項はA268754の2n番目の項の2倍になっているようでした。

2n+1番目に対応する振動物体は、全て斜め筒型(最初の2個の右側)になっていました。
残りの偶数番目の振動物体は、B2e/S型(最初の2個の左側)のものとそうでないものが混ざっていました。

B2e/S型になる項は、以下の表の赤い部分です。

どうやら2^m番目の項がB2e/S型になるようです。
B2e/S型でない振動物体は、よく観察すると「長い周期を持つ大き目の領域」と2周期の「小さい領域」になっています。(第12項のみ例外です)

余談ですが、B2e/S型でも斜め筒型でもない振動物体は初期状態から振動物体になるまでの世代数が異様に多く、特に第22項は28周期に落ち着くまでに130万世代ほど要しました。
また、このルールでは枠を作ってその中に適当にセルを置けば大抵振動物体になるので、根気さえあればいくらでも謎の数列を生み出すことができます。

最後に
明日のアドベントカレンダーはコロちゃんぬさんが「今日の推し関数について書きます」とのことです。
それではお楽しみに!
