どうも、108Hassiumです。
先週、こんな記事を投稿しました。
この記事ではもともと「バーニングシップフラクタルと関連するが名前がついていないもの」も紹介する予定でしたが、名前のあるものの紹介だけでかなりのボリュームになってしまいました。
というわけで、今回は先週の記事の没ネタを紹介します。
バーニングシップ変換
バーニングシップフラクタルは、複素数を用いると「$${(|\text{Re}(z)|+i|\text{Im}(z)|)^2+c}$$のマンデルブロ集合」($${\text{Im}(z)}$$と$${\text{Re}(z)}$$は$${z}$$の実部と虚部)と表すことができます。
なお、この記事では「マンデルブロ集合」という単語の定義として以下を用います。
以下の複素数列が無限大に発散しないような複素数$${c}$$全体の集合を、「$${f(z,c)}$$のマンデルブロ集合」とする。
$${z_{n+1}=f(z_{n},c)}$$
ただし、特に断らない限り$${z_0=0}$$とする。
また、この記事では$${z\rarr |\text{Re}(z)|+i|\text{Im}(z)|}$$という変換を「バーニングシップ変換」と呼び、$${B(z)}$$と表記することにします。
というわけで、いろいろな関数$${f(z,c)}$$について$${f(B(z),c)}$$のマンデルブロ集合を見ていきましょう。
☝B(z)^3+cのマンデルブロ集合
☝B(z)^4+cのマンデルブロ集合
☝B(z)^5+cのマンデルブロ集合$${B(z)^n+c}$$のマンデルブロ集合は、$${n}$$が奇数のときは線対称の軸を1本だけ持ち、偶数のときは非対称になるようです。
☝cB(z)+1のマンデルブロ集合1次関数のマンデルブロ集合は普通は全然面白くない形にしかならないのですが、バーニングシップ変換を噛ますことで少し面白そうな感じになります。
☝c/(B(z)^2-1)+1のマンデルブロ集合個人的にお気に入りの関数としてとして何度か紹介している$${\frac{c}{z^2-1}+1}$$ですが、バーニングシップ変換をするとまた違った面白さを見せてくれるようです。
☝B(z)^3+0.5+0.7iのジュリア集合
☝B(z)^3+0.51+0.09iのジュリア集合
☝B(z)^4+0.8iのジュリア集合
☝B(z)^4-0.1-0.6iのジュリア集合$${B(z)^n+c}$$のジュリア集合は実軸と虚軸について線対称(これは$${f(B(z))}$$という形の関数のジュリア集合全部に共通する性質っぽいです)で、次数の違いによる特徴は特に見当たりませんでした。
☝(-0.1+1.5i)B(z)+1のジュリア集合
☝(0.7+1.1i)B(z)+1のジュリア集合
☝(-1.4+0.8i)B(z)+1のジュリア集合
☝(-0.5+0.9i)B(z)+1のジュリア集合
☝(-0.5+0.6i)/(B(z)^2-1)+1のジュリア集合
☝(1.6+0.1i)/(B(z)^2-1)+1のジュリア集合
☝(1.3+0.05i)/(B(z)^2-1)+1のジュリア集合
☝(1.4-1.3i)/(B(z)^2-1)+1のジュリア集合
☝(1.34-0.8i)/(B(z)^2-1)+1のジュリア集合分解型複素数
$${j^2=1}$$を満たす実数でない数$${j}$$と実数$${x,y}$$を用いて$${x+yj}$$と表される数を、分解型複素数と呼ぶそうです。
分解型複素数でも複素数と同様にマンデルブロ集合を定義することができ、$${z^2+c}$$の分解型複素数版マンデルブロ集合の計算式は実数だけで表すと以下のようになります。
$${\begin{cases}x_{n+1}=x_n^2+y_n^2+a\\y_{n+1}=2x_ny_n+b\end{cases}}$$
なお、この記事では前述の複素関数によるマンデルブロ集合の定義のほかに、以下の実関数による定義も併用します。
以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体の集合を、「$${(f(x,y,a,b),g(x,y,a,b))}$$のマンデルブロ集合」とする。
$${\begin{cases}x_{n+1}=f(x_n,y_n,a,b)\\y_{n+1}=g(x_n,y_n,a,b)\end{cases}}$$
ただし、特に断らない限り$${x_0=y_0=0}$$とする。
☝(x^2+y^2+a,2xy+b)のマンデルブロ集合
☝(x^2+y^2-1,2xy)のマンデルブロ集合
☝(x^2+y^2-1.3,2xy)のマンデルブロ集合
☝(x^2+y^2-1.1,2xy+0.3)のマンデルブロ集合分解型複素数自体はバーニングシップフラクタルとはほとんど関係ありませんが、バーニングシップフラクタルの仲間にはこれらのフラクタル図形と似た特徴を持つものが存在します。
☝(x^2+y^2+a,2|xy|+b)のマンデルブロ集合
☝(x^2+y^2-0.2,2|xy|-0.9)のジュリア集合
☝(x^2+y^2-0.7,2|xy|-0.8)のジュリア集合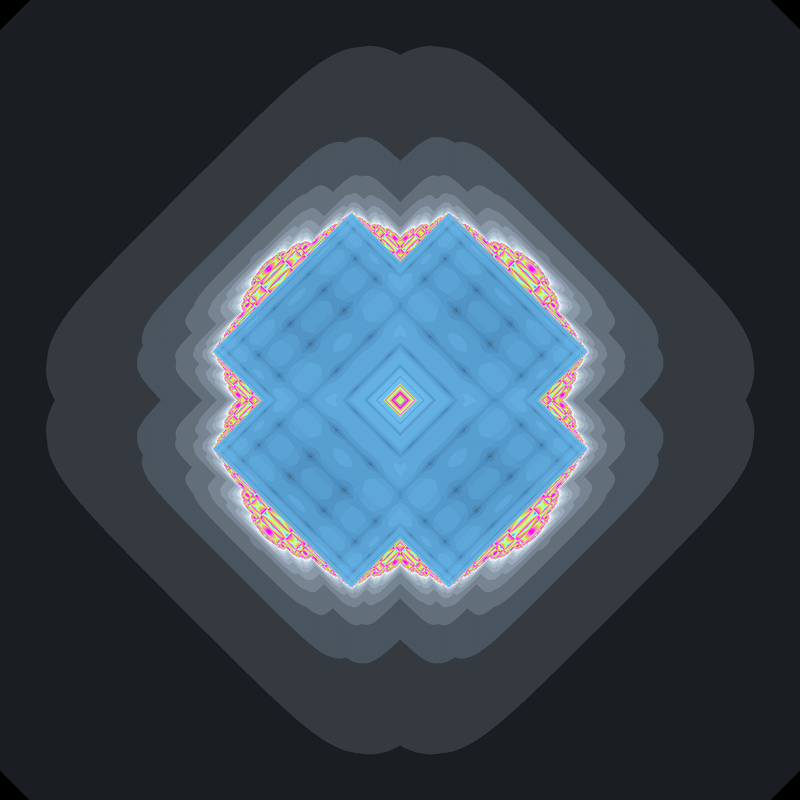
☝(x^2+y^2,2|xy|-0.7)のジュリア集合
☝(x^2+y^2-0.6,2|xy|+0.4)のジュリア集合
☝(x^2+y^2-1.1,2|xy|-0.4)のジュリア集合
☝(x^2+y^2-0.7,2|xy|-0.7)のジュリア集合
☝(x^2-|y^2-a|,2xy+b)のマンデルブロ集合
☝(x^2-|y^2-1.3|,2xy)のジュリア集合
☝(x^2-|y^2-0.3|,2xy+0.5)のジュリア集合
☝(x^2-|y^2-0.12|,2xy+0.6)のジュリア集合
☝(x^2-|y^2-0.1|,2xy+0.61)のジュリア集合
☝(x^2-|y^2-0.2|,2xy+0.8)のジュリア集合
☝(x^2-|y|y+a,2xy+b)のマンデルブロ集合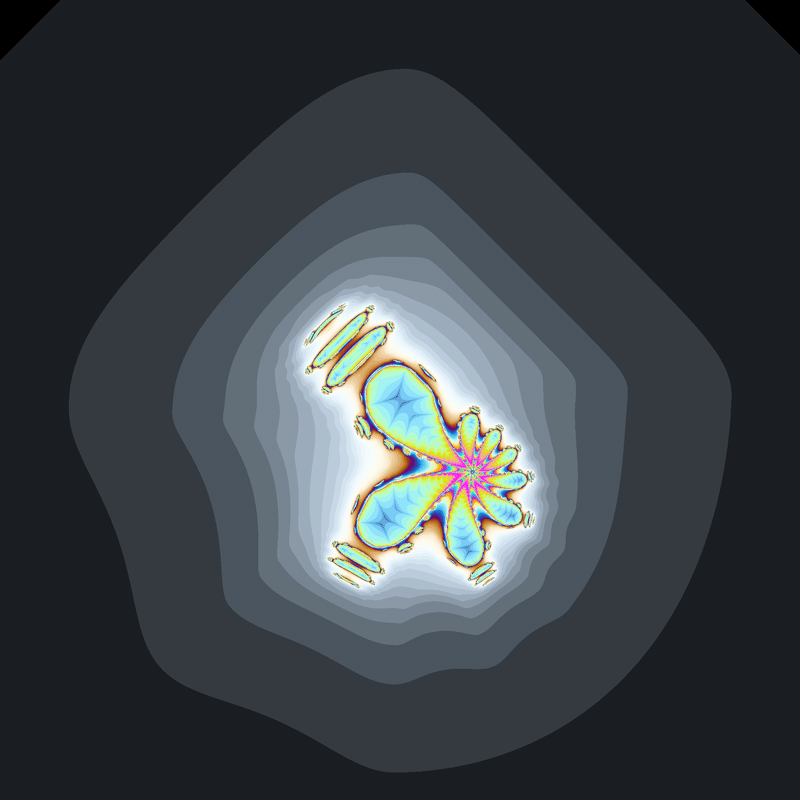
☝(x^2-|y|y+0.36,2xy+0.1)のジュリア集合
☝(x^2-|y|y-0.7,2xy+0.3)のジュリア集合
☝(x^2-|y|y-0.7,2xy-0.8)のジュリア集合
☝(x^2-|y|y-0.8,2xy+0.11)のジュリア集合
☝(x^2-|y|y-1,2xy-0.4)のジュリア集合
☝(-|x|x-y^2+a,2xy+b)のマンデルブロ集合
☝(-|x|x-y^2+1,2xy)のジュリア集合
☝(-|x|x-y^2+1.1,2xy+0.1)のジュリア集合
☝(-|x|x-y^2+1.19,2xy+0.1)のジュリア集合
☝(-|x|x-y^2+0.2,2xy+0.6)のジュリア集合
☝(-|x|x-y^2-0.51,2xy+0.51)のジュリア集合
☝(-|x|x-y^2-0.77,2xy+0.1)のジュリア集合因数分解
マンデルブロ集合の計算式に出てくる$${x^2-y^2}$$という部分は、ご存知の通り$${(x-y)(x+y)}$$と因数分解できます。
これを利用することでバーニングシップフラクタルの新たな仲間を発見できないか、ということを思いつきました。
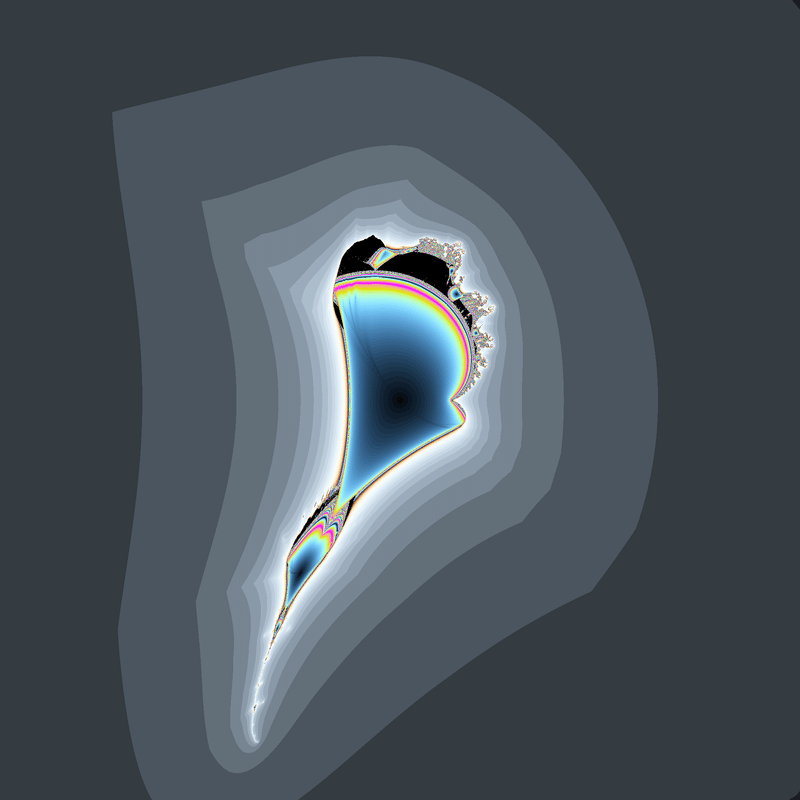☝(|x-y|(x+y)+a,2xy+b)のマンデルブロ集合
☝(|x-y|(x+y),2xy-0.75)のジュリア集合
☝(|x-y|(x+y),2xy+0.3)のジュリア集合
☝(|x-y|(x+y)+0.36,2xy+0.1)のジュリア集合
☝(-|x-y|(x+y)+a,2xy+b)のマンデルブロ集合
☝(-|x-y|(x+y)-0.6,2xy-0.7)のジュリア集合
☝(-|x-y|(x+y)+0.4,2xy+0.38)のジュリア集合
☝(-|x-y|(x+y)-0.92,2xy-0.25)のジュリア集合
☝(-|x-y|(x+y)+0.25,2xy+0.51)のジュリア集合
☝(-|x-y|(x+y)-0.51,2xy-0.51)のジュリア集合
☝((|x|-y)(x+y)+a,2xy+b)のマンデルブロ集合
☝((|x|-y)(x+y)+0.2,2xy+0.6)のジュリア集合
☝((|x|-y)(x+y),2xy+0.8)のジュリア集合
☝((|x|-y)(x+y)+0.3,2xy+0.5)のジュリア集合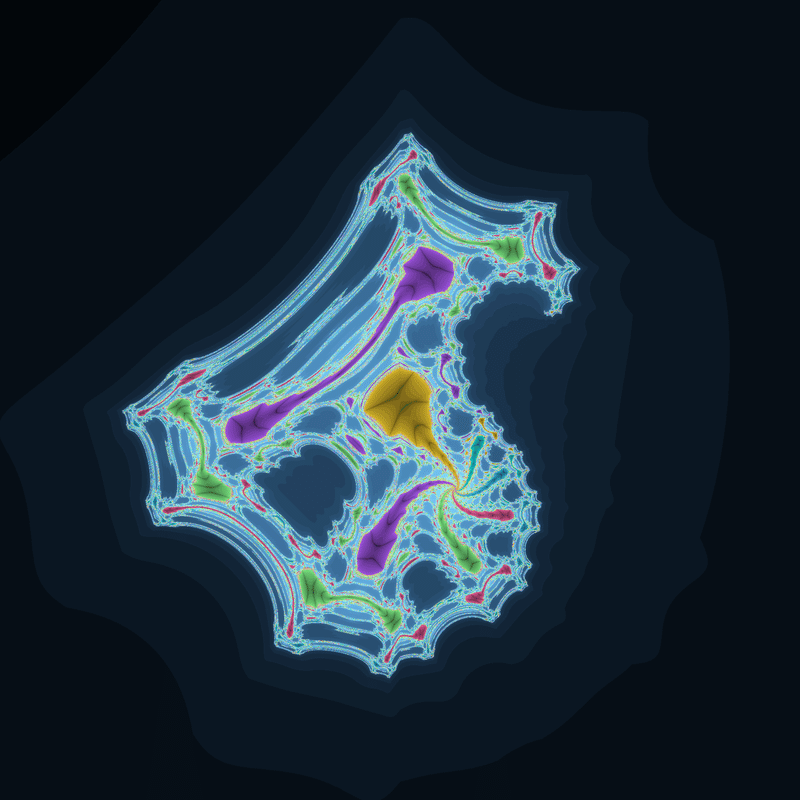
☝((|x|-y)(x+y)+0.4,2xy+0.2)のジュリア集合
☝((|x|-y)(x+y)+0.36,2xy-0.11)のジュリア集合
☝((|x|-y)(x+y)+0.11,2xy+0.7)のジュリア集合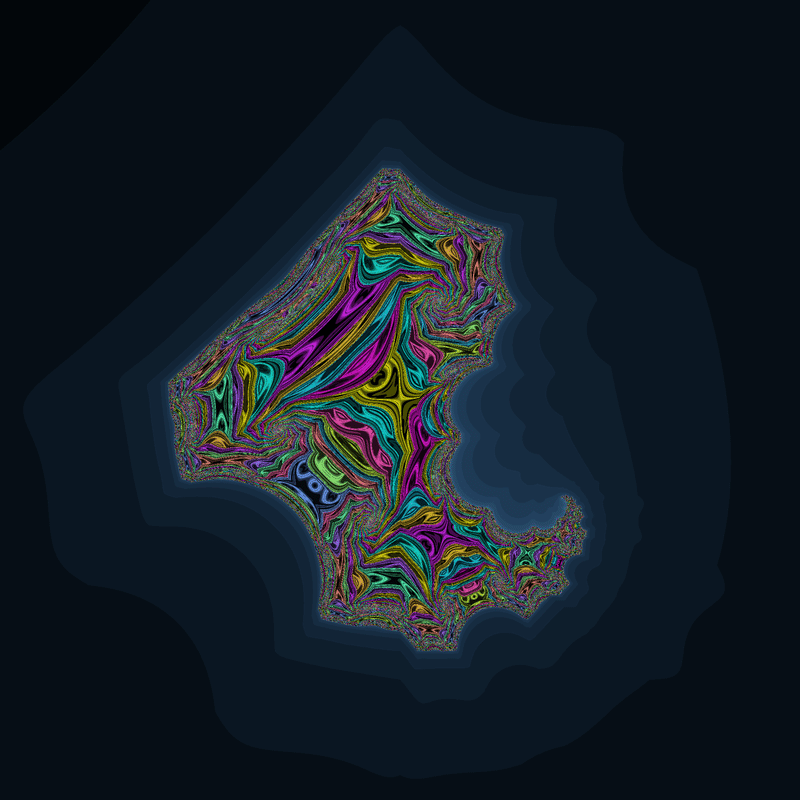
☝((|x|-y)(x+y)+0.4,2xy-0.3)のジュリア集合
☝((|x|-y)(x+y)+0.34,2xy+0.4)のジュリア集合
☝((x-|y|)(x+y)+a,2xy+b)のマンデルブロ集合
☝((x-|y|)(x+y)-0.2,2xy+0.8)のジュリア集合
☝((x-|y|)(x+y)+0.24,2xy+0.51)のジュリア集合
☝((x-|y|)(x+y)-0.38,2xy+0.6)のジュリア集合
☝((x-|y|)(x+y)-0.7,2xy+0.3)のジュリア集合
☝((x-|y|)(x+y)-1.27,2xy+0.02)のジュリア集合
☝((x-y)(x+|y|)+a,2xy+b)のマンデルブロ集合
☝((x-y)(x+|y|)+0.3,2xy+0.5)のジュリア集合
☝((x-y)(x+|y|)+0.24,2xy+0.51)のジュリア集合
☝((x-y)(x+|y|)-0.6,2xy+0.47)のジュリア集合
☝((x-y)(x+|y|)-0.4,2xy+0.59)のジュリア集合
☝((x-y)(x+|y|)-0.62,2xy+0.4)のジュリア集合
☝((x-y)(x+|y|)-0.8,2xy-0.13)のジュリア集合その他
☝(x^2-xy+a,y^2+xy+b)のマンデルブロ集合$${(x^2-xy+a,y^2+xy+b)}$$のマンデルブロ集合は、式の形が似ていない上に絶対値関数を使っていないにもかかわらず、どことなくバーニングシップフラクタルと似ています。
☝(x^2-xy-1,y^2+xy-0.4)のジュリア集合
☝(x^2-xy-0.75,y^2+xy+0.75)のジュリア集合
☝(x^2-xy-0.9,y^2+xy-0.6)のジュリア集合
☝(x^2-xy-0.8,y^2+xy-0.87)のジュリア集合
☝(x^2-xy-0.75,y^2+xy-0.86)のジュリア集合ジュリア集合は$${(x^2-y^2+a,2|xy|+b)}$$のものと同じく対称軸を2本持つのですが、何故か中途半端な角度(多分22.5°)に傾いています。
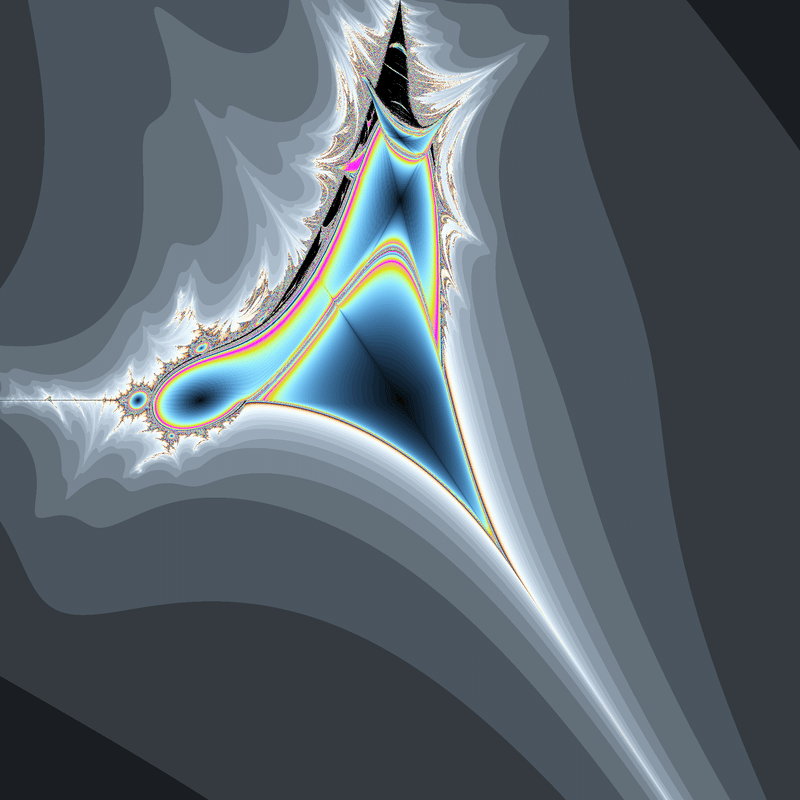☝(x^2-xy+a,y^2-2xy+b)のマンデルブロ集合このマンデルブロ集合は、左側に$${z^2+c}$$のマンデルブロ集合やmandelbarに似た形が見えます。
もはやバーニングシップフラクタルとは全然関係ありませんが、何となく繋がりを感じるのでオマケとして紹介します。
☝(x^2-xy,y^2-2xy-1.3)のジュリア集合
☝(x^2-xy-1,y^2-2xy+0.16)のジュリア集合
☝(x^2-xy-0.7,y^2-2xy-0.4)のジュリア集合
☝(x^2-xy+a,2xy-y^2+b)のマンデルブロ集合
☝(x^2-xy+0.33,2xy-y^2+1.5)のジュリア集合
☝(x^2-xy+0.7,2xy-y^2+1.16)のジュリア集合
☝(x^2-xy+0.6,2xy-y^2+0.14)のジュリア集合
☝(x^2-xy+0.63,2xy-y^2+1.14)のジュリア集合
☝(x^2-xy-0.9,2xy-y^2-0.1)のジュリア集合
☝(x^2-xy-0.9,2xy-y^2-0.2)のジュリア集合追記
☟続き？
