
バーニングシップフラクタルと仲間たち3
どうも、108Hassiumです。
以前、こんな記事を書きました。
1本目の記事ではバーニングシップフラクタルと同じ「$${z^2+c}$$と絶対値関数を組み合わせてできるフラクタル図形」のうち有名なものを紹介し、2本目の記事ではマイナーなものを紹介しました。
そして最近になってバーニングシップフラクタル関連図形の新たなグループを発見したので、この記事ではそれらを全て紹介したいと思います。
レア
今回紹介したいグループは内部でさらに3つの小グループに分かれているので、一応各グループに名前を付けておきました。
なお、そのグループ内の個別のフラクタル図形に対しては名前は付けていません。
(x+iy)(x+i|y|)+c

この記事で紹介するのは、$${(\alpha+i\beta)(\alpha+i\beta)+c}$$に対して以下の変換を適用したものです。
$${\alpha\rightarrow x}$$
$${\alpha\rightarrow -x}$$
$${\alpha\rightarrow |x|}$$
$${\alpha\rightarrow -|x|}$$
$${\beta\rightarrow y}$$
$${\beta\rightarrow -y}$$
$${\beta\rightarrow |y|}$$
$${\beta\rightarrow -|y|}$$
ただし、絶対値関数を使った変換の使用回数は1回から3回までとします。
このルールで生成できる式は$${4^4-2^4×2=224}$$通り存在しますが、簡単な式変形で同じ関数だと示せるものや生成されるマンデルブロ集合が同じ形になるものを同一視していくと20種類になりました。
(x-iy)(x+i|y|)+c

$${(-x-i|y|)(-x+iy)+c}$$という関数のマンデルブロ集合はこれと全く同じ形ですが、これは
$${(-x-i|y|)(-x+iy)\\=(-x+iy)(-x-i|y|)\\=-(x-iy)(-x-i|y|)\\=(x-iy)(x+i|y|)}$$
・・・という式変形が可能であり、$${(-x+iy)(-x-i|y|)+c}$$と$${(x-iy)(x+i|y|)+c}$$が同一の関数であることが原因です。
このような「見た目が違うけど実質同じ関数」を避けるため、この記事のための事前調査(今回紹介するグループに含まれるすべてのフラクタル図形を洗い出すためのもの)では「絶対値関数はなるべく式の後ろの方に置く」「式の一番最初の$${x}$$の符号はプラスで固定」というルールを設け、調査対象を絞り込みました。
(x+iy)(|x|+iy)+c

(x+iy)(-|x|+iy)+c

(x-iy)(|x|+iy)+c
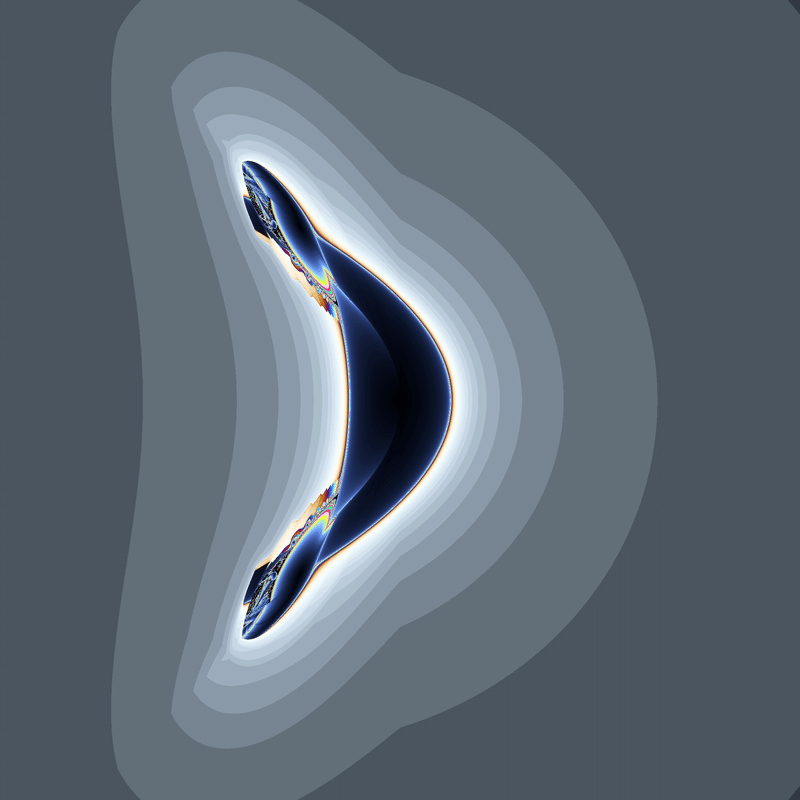
(x-iy)(-|x|+iy)+c
ミディアム
小グループの分類は絶対値関数の使用回数が基準になっており、グループ名は絶対値が1個のものから順にレア、ミディアム、ウェルダンです。(バーニングシップフラクタルは絶対値関数が4個なので、「火に関係する」「順序がある」という理由で選びました)
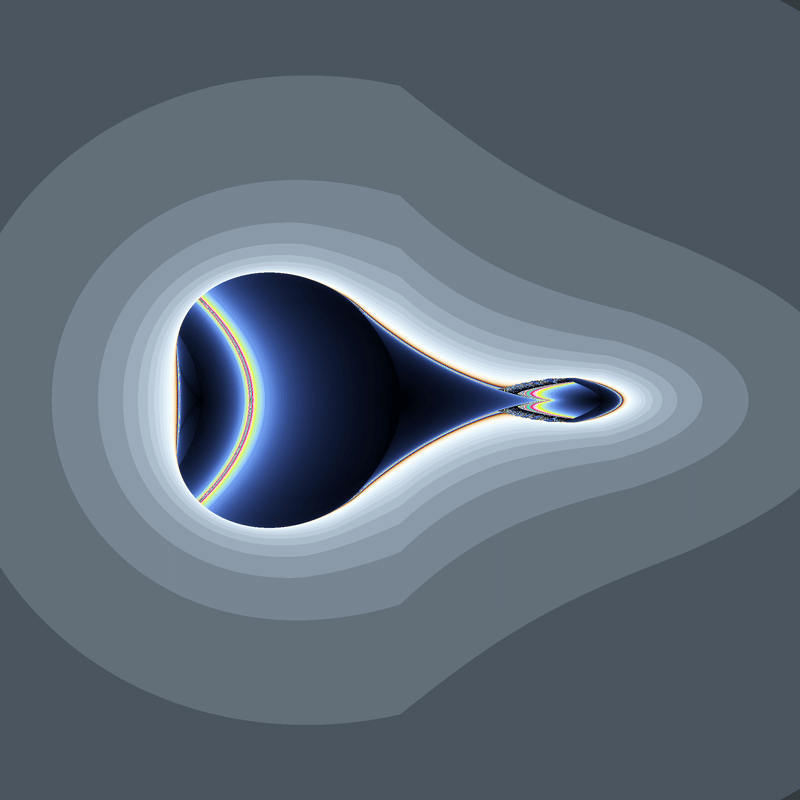
(x+iy)(|x|+i|y|)+c

(x+iy)(-|x|+i|y|)+c

(x-iy)(|x|+i|y|)+c

(x-iy)(-|x|+i|y|)+c
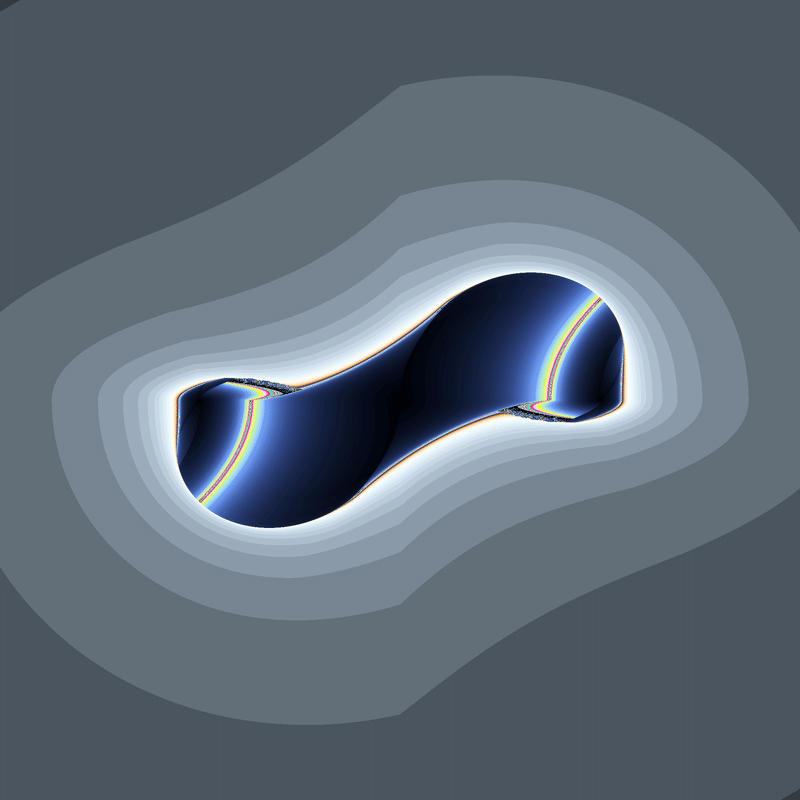
ミディアムグループのうち、絶対値関数が後半に固まっているものは全て点対称なマンデルブロ集合になるようです。
また、逆に今回紹介するもののうち点対称なものはこのグループの4つのみでした。
(x+i|y|)(x+i|y|)+c

以前の記事で紹介した「Perpendicular Burnig ship」です。
(x+i|y|)(x-i|y|)+c

この図形だけちょっと特殊で、絶対値関数の位置が異なる$${(|x|+iy)(|x|-iy)+c}$$等と同じ形になります。
(x+i|y|)(|x|+iy)+c

(x+i|y|)(-|x|+iy)+c
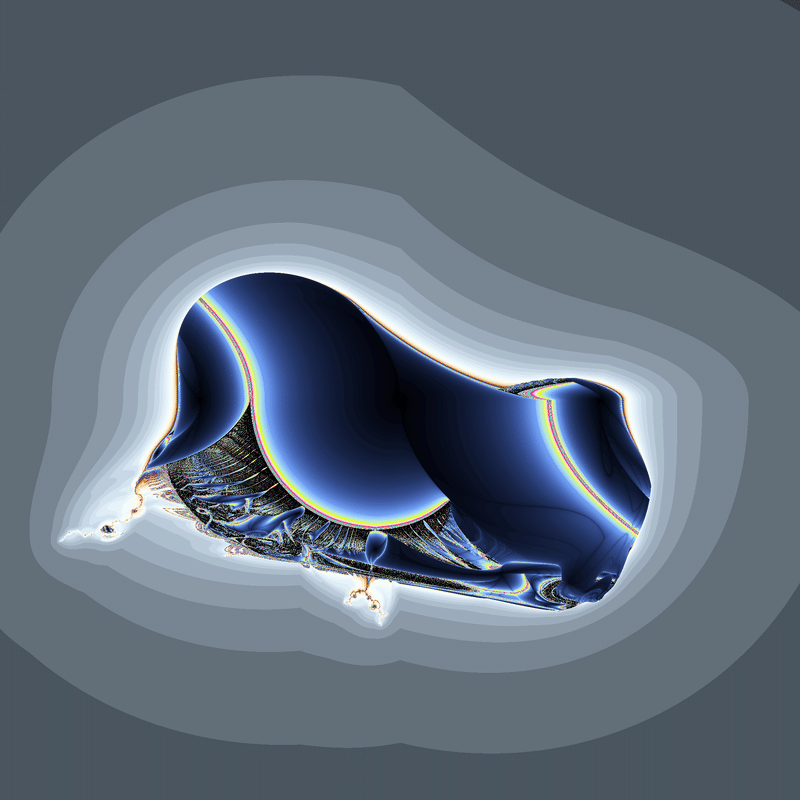
(|x|+iy)(|x|+iy)+c

以前の記事で紹介した「Heart Mandelbrot」です。
(|x|-iy)(|x|-iy)+c

以前の記事で紹介した「Perpendicular Mandelbrot」です。
ウェルダン
(x+i|y|)(|x|+i|y|)+c

(x+i|y|)(-|x|+i|y|)+c
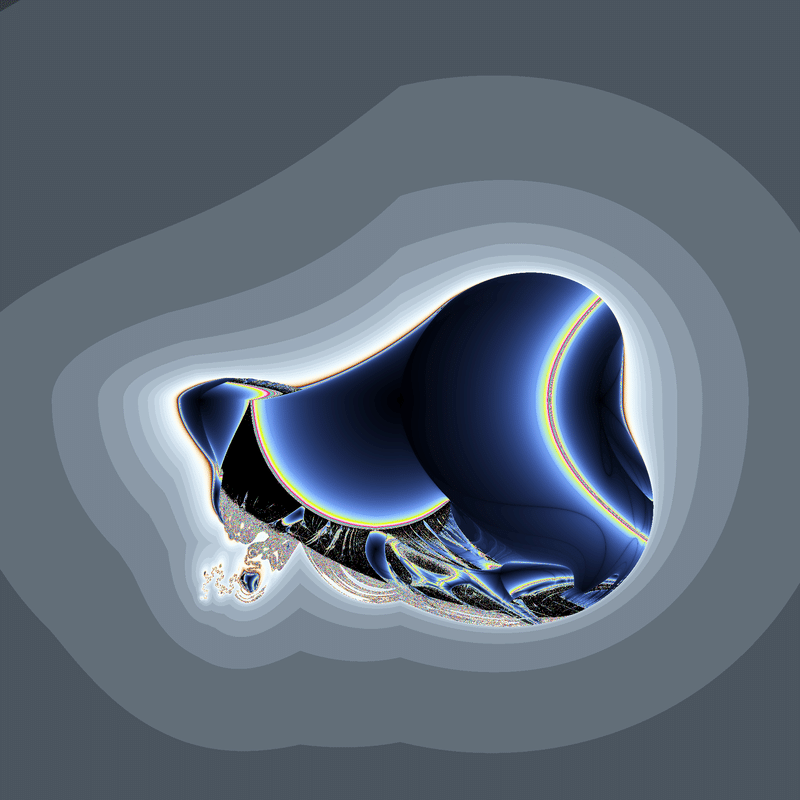
(|x|+iy)(|x|+i|y|)+c

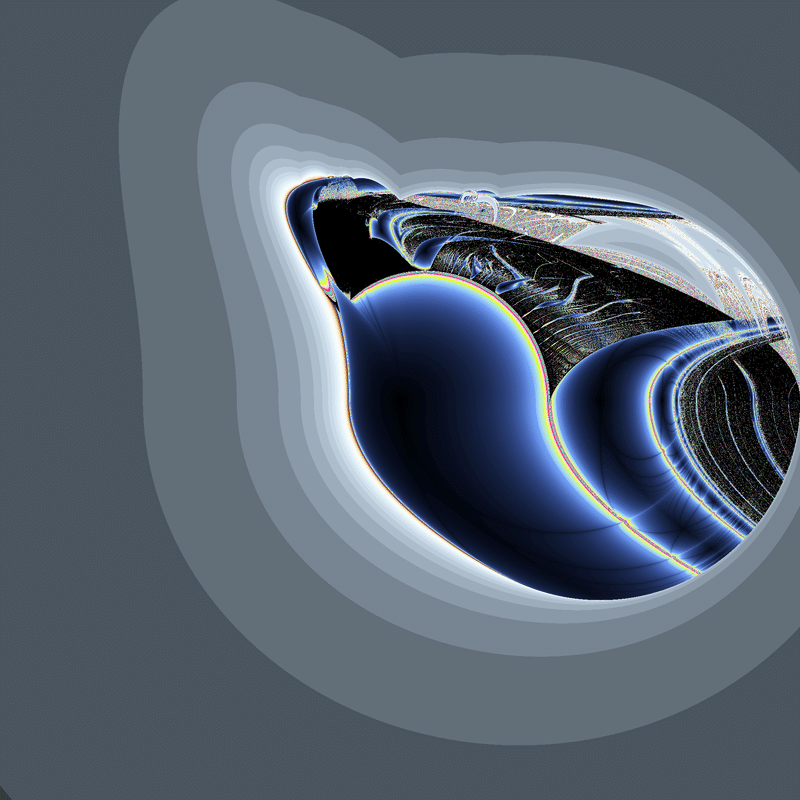
(|x|+iy)(-|x|+i|y|)+c
おまけ

各グループの系統図です。
0と1の部分は絶対値関数の位置関係を表し、その後の数値は生成可能な式の本数、最後が実際に得られるマンデルブロ集合の個数です。

「ちょっと特殊」と説明した$${(x+i|y|)(x-i|y|)+c}$$の正体です。
$${(x+i|y|)(x-i|y|)}$$と$${(|x|+iy)(|x|-iy)}$$を展開するとそれぞれ$${x^2+|y|^2}$$と$${|x|^2+y^2}$$になり、$${|r|^2=r^2}$$なのでどちらも同じマンデルブロ集合になるというわけです。
