
アインシュタインタイルを1列に並べた「GSE」を愛でてみる、つもりですがまだ愛でない。
前回の記事はこちら。
アインシュタインタイルマスでくみたてたほぼ菱形盤面を紹介しました。
で、この盤面について1つスルーしたポイントがあります。
ところでhexにはこのようなTを二つGSEで繋いだボードはいかがでしょうか?
— Yoshiaki Araki 荒木義明 (@alytile) August 15, 2023
4×4と12×12のボードを作ってみました。 pic.twitter.com/xxRWuQzbf0
ところでhexにはこのようなTを二つGSEで繋いだボードはいかがでしょうか? 4×4と12×12のボードを作ってみました。
GSE。
菱形盤面の中央を貫く、アインシュタインタイルマスの並びです。

【追記】
厳密に言うと、並んだ図形の一部がGSEがあります。
今回は、GSEを愛でてみます(というか、予定)。
GSE?
GSE。
論文「An alternative proof for an aperiodic monotile」の11ページに”Golden Sturmian Edge(黄金スターミアン辺)”の表記があります。
頭文字でGSE。
Golden、Edgeはいいとして……あの、Sturmianってなんでしょうか。
調べてみると英語版ウィキペディアで「Sturmian Word」の項目が見つかりました(日本語はなし)。
和訳すると「スターミアン文字列」。
簡単に説明すると、2つの文字(1と0、aとb、とか)があるルールに従って無限に並ぶ文字列です。
スターミアン文字列の前に……
スターミアン文字列の具体的な例を1つあげます。
それが「Fibonacci word」で、日本語版ウィキペディアだと「フィボナッチ列」の項目があります。
【引用】
フィボナッチ列(フィボナッチれつ、Fibonacci word)とは、フィボナッチ数の加算の代わりに文字列連結を用いて得られる2進列(または2種類のアルファベットからなる文字列)である。 フィボナッチ文字列とも呼ばれる。
1、1、2、3、5、8、13、23……と続くフィボナッチ数(フィボナッチ数列)を知っている人は多いと思いますが、それとは異なります(とはいえ、全く関係ないわけではないのですが、その点は後述)。
フィボナッチ列は、以下のルールに沿って作ることのできる無限個の文字からなる文字列です。
$${S_0=0, S_1=01, S_{n}=S_{n-1}S_{n-2}}$$
最初の数個の項は
第0項 0
第1項 01
第2項 010 (第1項「01」と第0項「0」を連結して並べる)
第3項 01001 (第2項「010」と第1項「01」を連結)
第4項 01001010 (以下同)
第5項 0100101001001
…………
となります(第∞項がフィボナッチ列)。
左から右に2つの文字(0と1)が並ぶ順序は変わらず、次々と新たに追加されていきます。
さほど複雑なルールではないです。
ところで、フィボナッチ列の各項の文字数をみると、
1、2、3、5、8、13、……
と続き、この並んだ数値の列はフィボナッチ数列になっています。
スターミアン文字列、またの名を……
下の図のように、平面グラフにフィボナッチ列(0100101001001……)の2つの文字の出現に合わせて長さ1の線分(0は縦、1は横に。異なる文字の連結は端点がつながり、同じ文字の連結は平行にずれる)をならべます。

さて、これらの線分を左下(平面グラフの原点)から出発して、スキーの関門に見立ててすべてを通り抜けてみます。
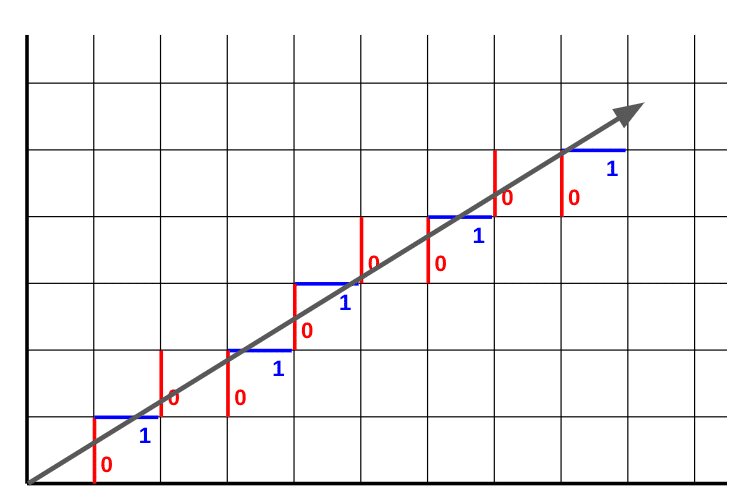
思いっきり、直滑降。
一直線ズドーン。
【補記】
上の図では第5項までの文字しか並べていませんが、それ以降無限に並べた場合も、一直線にズドドドドーン、です。
さらにいえば、直滑降の軌跡は真っ直ぐシンプルな一次関数(f(x)=ax : aは定数)で表すことができます。
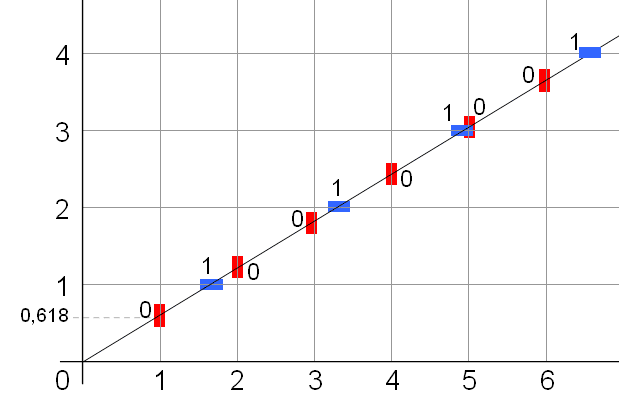
https://en.wikipedia.org/wiki/Sturmian_word#/media/File:Fibonacci_word_cutting_sequence.png
その傾き、aの値は0.618……になります。
ここでピンとくる人は、その値に1を加えます。
1.618……は、黄金比の値です。
平面グラフで引いた直線ですが、これを線分の長さ1の正方形状のビリヤード台で球を撞いて反射しながらずっと転がり続ける(下の図)のように、閉空間に畳んでしまう表現もできます。

反射しまくります
フィボナッチ列の第0項(0)と第1項(01)の値が変われば、ビリヤード台での反射する球の動きの角度(傾き)も変わります。
逆に、球の動きの角度によって、第0項と第1項が定まります。
なので、スターミアン文字列を、ビリヤード数列とも呼んだりします。
とりあえず一旦の締め
で、いよいよ本題である論文に登場するGSE……ですが、フィボナッチ列で結構な分量になったので、いったんここで休憩。
次回に愛でます。
そのつもりです。
では。
