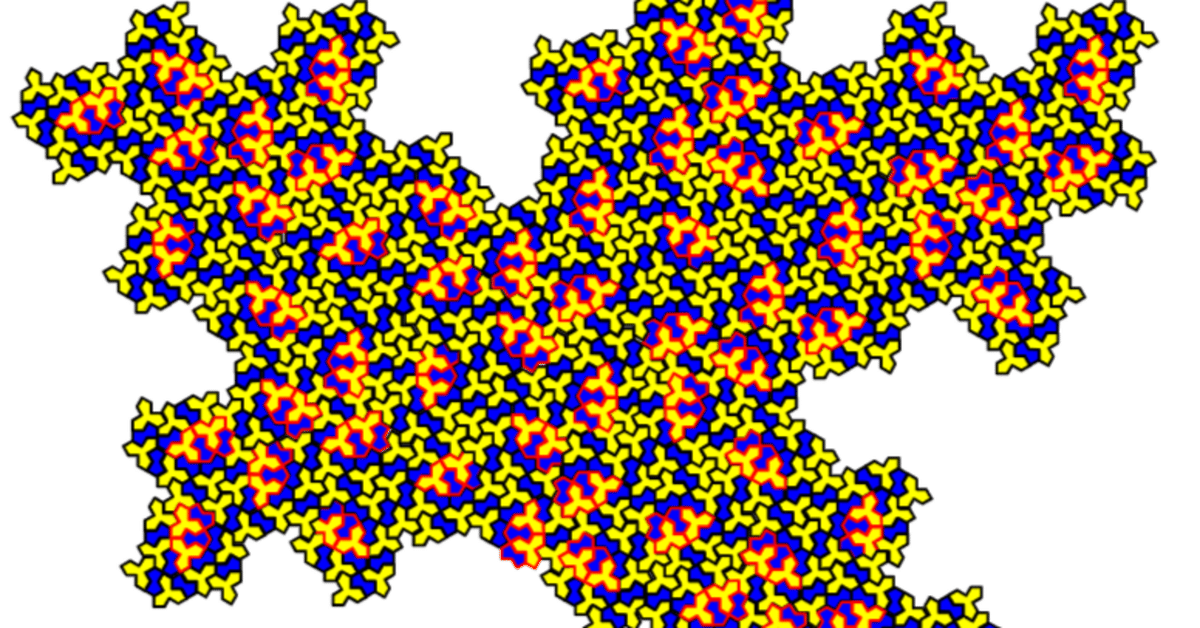
アインシュタインタイルを配置した「お花畑」を愛でてみる。とにかく愛でてみる。
やるやると言っておきながら、伸ばし伸ばしにしておりました、アインシュタインタイルの話題でございます。
そちらの前回の記事はこちら。
今回は、記事の最後に予告したことをやってみます。
ヘリコプターをSPECTREで敷き詰める
することは単純といえば単純。
SPECTRESの配置パターンでタイルを敷き詰めるだけです。
ただし、敷き詰めるタイルは

左の方のTile(1,1)、ではなく、右のタイルTile(1,1)を2つの点対称図形に分割したヘリコプターになります。
下の図は、論文「A chiral aperiodic monotile」の6ページにある配置パターンを元にしたものになります。

この配置パターンを使って、左の配置に適用すると、

右の配置になりまして、それをまた配置パターンを適用すると

こうなります(※手作業なので、間違ってたらごめんなさいね)。
回転主翼のお花畑やー
さてさて、タイルの大きさが小さく細かいので分かりづらいかも知れませんが、黄色の回転主翼に注目すると、ところどころ密集しているのが確認できます。
特徴を踏まえて、個人的に色分けをしてみるとこのようになります。

色塗りをしているのは、確定している内側の回転主翼になります。
これを一部拡大したのが、前回の記事の最後に示したものです。

さて、その特徴ですが
◆黄色のままにしているのは、回転主翼が正三角形上に6個密集しています。
◆オレンジと水色は、回転主翼が正三角形上に3個密集しています。
◆赤と緑は、回転主翼が1個単独です。
さらに加えると、
◇赤とオレンジは、他の回転主翼と接しています。
◇緑と水色は、他の回転主翼と接せずに独立しています。
つまり、密集パターンは5通り(大きく3通り)あります。
あと、回転主翼の塗り分けで混乱するので、MISTICとなる2つのタイルを他のタイルと区別しませんでした。
では、MISTICの回転主翼はどうなっているかと言うと、1つは赤に確定します。

おそらく、回転主翼の密集パターンは、SPECTREの配置パターン3回目で固定しているようにみえます。
なので、2回目のSPECTREの配置パターンで回転主翼のパターン分けを示すことができると思われます。

上が通常2回目で、下がMISTICの2回目配置パターンです(※これも手作業なので、間違っているおそれあります)。
左側は、黄色の回転主翼は(黃・オレンジ・水色の可能性があるので)未確定の状態です。
興味深いのは、MISTICの左の配置パターンで、この時点で1箇所緑が確定しています。
オレンジと水色は、複数の配置パターンが接して構成されますが、上の図のように固定されているようです(※あくまでも予想)。
ヘリコプターをHATで敷き詰める
さて、そうなるともう一方の元祖HATの敷き詰めのほうもどうなっているのか気になります。
論文「An aperiodic monotile」の18ページにある配置パターンを元にして、途中の過程をすっ飛ばしまして、同様のタイルを敷き詰めるとこうなります。

同じように、回転主翼を色分けすると下になります。

こちらは、端の回転主翼も色分けしてみましたが、水色(正三角形上に3個密集しつつ他の回転主翼と独立している)がありません。
ちなみに、HATの配置パターンのH₇、H₈の双方に赤となる回転主翼は裏返っているタイルにあります。
さらに、H₇の固定した箇所にある回転主翼は緑になります。

SPECTREとHATの配置パターン、双方の相違点としては興味深い情報かもしれません。
ヘリコプターをGOLDEN HEXパターンで敷き詰める
もうひとついきます。
これらの記事で紹介した、論文「An alternative proof for an aperiodic monotile」の2ページにある敷き詰めパターン(Golden Hex Substitutions)も見てみますよ。
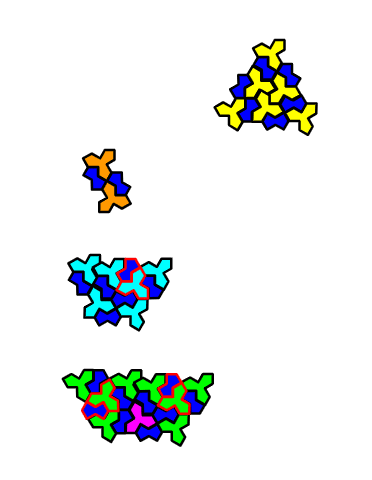
上から、T₂(黃)、PD₁(オレンジ)、ZD₁(水色)、ZT₁(緑・紫)となります。
回転主翼の色分けは、それぞれ4種類のグループに分けています。
枠が赤いタイルは裏返しになっています。
ZTに1つだけ紫がありますが、これは他の回転主翼と接せずに独立しているからです。
これらを配置パターンで組み上げていくのですが、たとえばZD₃は下のようになります。
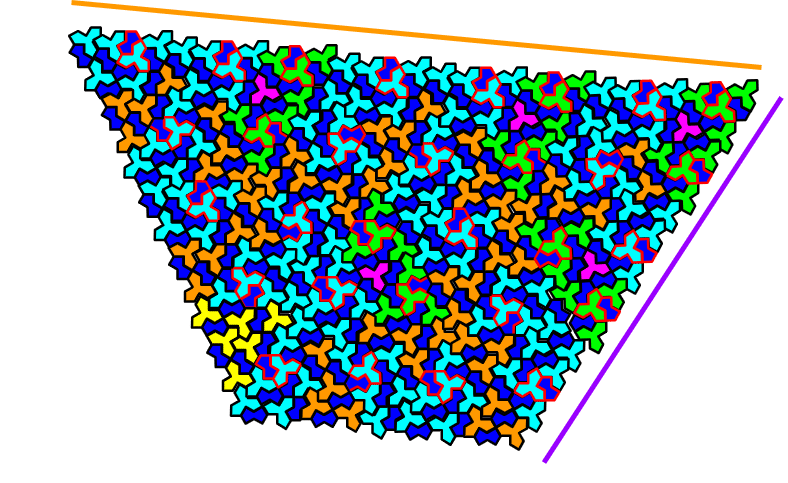
オレンジとラベンダーの線をZD₃の外側に引きましたが、それに沿うZD₃の端の列は、以前の記事で書いた「GSP」「GSE」になります。
「GSP」「GSE」は特定のスターミアン文字列で導き出すことが出来ますが、その文字列において同じ文字は連続で最大3つまでしか並びません。
回転主翼の密集パターンの最大のものは、正三角形上で6個、つまり1辺で3個なのです。
ここでも、しっかり関係しているのですね。
締めと今後?
結構お腹いっぱいになってきたので、今回はこの辺で。
来月より「アブストラクトAdvent Calendar2023」に力を入れるので、アインシュタインタイルについては来年に持ち越す予定です。
……来年、ってまだ書くことあるんかい。
いや、ありそうなんですよ。
今回はTile(1,1)という、HATシリーズのなかでも特別な図形で敷き詰めてみたのですが、もっと特殊な図形があるのです。
こいつらです。

右:Tile(1,0)またの名をComet
また、そのうち。
では。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
