【解説】早稲田大学理工数学2024[II]

問題

$${n}$$を自然数とし，数$${1, 2 ,4}$$を重複を許して$${n}$$個並べてできる$${n}$$桁の自然数全体を考える。そのうちで$${3}$$の倍数となるものの個数を$${a_{n}}$$，$${3}$$で割ると$${1}$$余るものの個数$${b_{n}}$$，$${3}$$で割ると$${2}$$余るものの個数$${c_{n}}$$とする。

(1) $${a_{n+1}}$$を$${b_{n}, c_{n}}$$を用いて表せ。同様に，$${b_{n+1}}$$を$${a_{n}, c_{n}}$$を用いて，$${c_{n+1}}$$を$${a_{n}, b_{n}}$$を用いて表せ。
(2) $${a_{n+2}}$$を$${n}$$と$${c_{n}}$$を用いて表せ。
(3) $${a_{n+6}}$$を$${n}$$と$${c_{n}}$$を用いて表せ。
(4) $${a_{6m+1}\ (m=0,1,2,…)}$$を$${m}$$を用いて表せ。

解説

記述を簡略化するため、数$${1, 2 ,4}$$を重複を許して$${n}$$個並べてできる$${n}$$桁の自然数のうち、$${3}$$の倍数となるもの全体の集合を$${A_{n}}$$、$${3}$$で割ると$${1}$$余るもの全体の集合を$${B_{n}}$$、$${3}$$で割ると$${2}$$余るもの全体の集合を$${C_{n}}$$とおきます。

(1)

自然数を$${3}$$で割った余りは各桁の和を$${3}$$で割った余りと等しいことを思い出すと、$${A_{n}}$$(余り$${0}$$)の要素の末尾に$${1}$$または$${4}$$を加えた$${n+1}$$桁の自然数はすべて$${B_{n+1}}$$(余り$${1}$$)の要素となります。同様に、$${A_{n}, B_{n}, C_{n}}$$の要素の末尾に$${1,2,4}$$を追加した自然数が、$${A_{n+1}, B_{n+1}, C_{n+1}}$$のどこに属すかを整理すると以下の図のようになります。

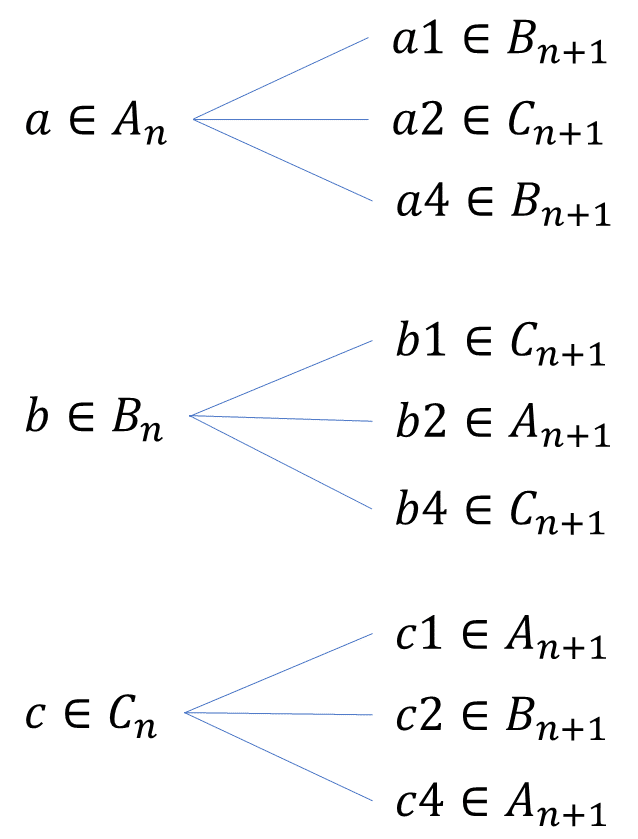
これより

$$
\bm{a_{n+1} = b_{n} + 2c_{n}}\\
\bm{b_{n+1} = c_{n} + 2a_{n}}\\
\bm{c_{n+1} = a_{n} + 2b_{n}}
$$

となります。

(2)

(1)の漸化式と、自明な関係式

$$
a_n + b_n + c_n = 3^n
$$

を用いて、$${a_{n+2}}$$を$${c_{n}}$$と$${n}$$のみになるよう計算していくと

$$
\begin{array}{lll}
a_{n+2} &=& b_{n+1} + 2c_{n+1}\\
&=& c_{n} + 2a_{n} + 2(a_{n} + 2b_{n})\\
&=& 4(a_{n} + b_{n}) + c_{n}\\
&=& 4(3^{n}-c_{n}) + c_{n}\\
&=& \bm{4\cdot3^n - 3c_n}
\end{array}
$$

となります。

(3)

(1)の3つの連立漸化式は$${a_{n}\to b_{n}, b_{n}\to c_{n}, c_{n}\to a_{n},}$$という交換に対して対称だから、(2)と同様にして

$$
\begin{array}{lll}
b_{n+2} &=& 4\cdot3^n - 3a_n\\
c_{n+2} &=& 4\cdot3^n - 3b_n
\end{array}
$$

が得られます。これを繰り返し使うと

$$
\begin{array}{lll}
a_{n+6} &=& 4\cdot3^{n+4} - 3c_{n+4}\\
&=& 4\cdot3^{n+4} - 3\left(4\cdot3^{n+2} - 3b_{n+2}\right)\\
&=& 4\cdot3^{n+4} - 4\cdot3^{n+3} +9\left(4\cdot3^{n} - 3a_{n}\right)\\
&=&4\cdot3^{n+2}(9-3+1)-27a_{n}\\
&=&\bm{28\cdot3^{n+2}-27a_n}
\end{array}
$$

が得られます。

(4)

$${a_{6m+1}}$$を求めるには、(3)の漸化式において$${n=6m+1}$$として得られる$${m}$$についての漸化式

$$
{a_{6(m+1)+1}} = 28\cdot3^{6m+3}-27a_{6m+1}
$$

を解けばよいです。両辺$${3^{6(m+1)}}$$で割り、$${d_m=a_{6m+1}/3^{6m}}$$とすると

$$
\begin{array}{lll}
d_{m+1} &=& \cfrac{28}{3^3} - \cfrac{d_{m}}{3^3}\\
&=&d_{m+1} - 1 = -\cfrac{1}{27}\left(d_{m}-1\right)\ (\because a_1=0)
\end{array}
$$

となるので、$${d_{m}-1}$$は公比$${-1/27}$$等比数列です。よって

$$
\begin{array}{lll}
d_{m} &=& (d_{0}-1)\left(-\cfrac{1}{27}\right)^{m} + 1\\
&=&\left(\cfrac{a_{6\cdot0+1}}{3^{6\cdot0}}-1\right)\left(-\cfrac{1}{27}\right)^{m} + 1 \\
&=&1 - \left(-\cfrac{1}{27}\right)^{m}
\end{array}
$$

であり、

$$
a_{6m+1} = 3^{6m}d_m = \bm{3^{6m} - (-3)^{3m}}
$$

となります。