#1 【非日常の数学】 ゾンビはどれくらいのペースで増えていくのか？

日常の中の非日常を、数式で表してみるとどうなるかを考えてみました。今回はゾンビの数についての数式です。

※ いわゆるギャグ的な内容ですので、ゆる〜くお楽しみください。
※ note内では数式を画像化して表示しているため、大きさにバラツキがあり見にくいと感じることがあるかもしれません。
※ 本内容をPDFでキレイにまとめたものを本文の最後にリンク掲載していますので、そちらもぜひ御覧ください。
※ 本文は全て読めますが、「投銭」として最後に購入ボタンを設定していますので、気に入っていただけましたら応援宜しくお願いします。

はじめに

　ゾンビものの映画やドラマを観ていると、きっと誰しもが、一度は「一体どれくらいのペースでゾンビは増えていくんだろう」と疑問に思ったことだろう。そこで本著では、そうした疑問を解決するために、一定の仮定の下でのゾンビ数を計算し、その式を示している。

　ただし、残念ながら本著ではゾンビ数を計算するのみで、人類を救う方法までは検討していない。生き残るためには、逃げるか、戦うしかない。

1. ゾンビの数はどれくらい？

　ゾンビはある日突然発生し、その数を増やしていく。噛まれるだけ、あるいは引っ掻かれるだけでその人もまたゾンビになってしまうというのは非常に厄介だ。そして、一度ゾンビになってしまうと、もはや自然に治ることはない。そのため、ゾンビの数は増える一方だ。では実際の数はいくらになるのだろうか？ただ逃げ続ける場合と、ゾンビと戦う場合とでそれぞれを考えてみることにする。

1.1 ただ逃げ続ける場合

　時刻 t におけるゾンビ数を z(t) で表すとしよう。ゾンビはいつも無数にいるイメージしかないかもしれないが、実際には「はじめのゾンビ」が存在するはずなので、時刻 0 におけるゾンビ数を a としよう（はじめは１人、すなわち a = 1 としても良いが、同時多発的に発生した場合を考えてみる）。そして、各ゾンビは、単位時間あたりに r 人に噛み付いて、新たなゾンビを作り出すと仮定する。

　ただ逃げ続ける場合のゾンビ数の式はシンプルで、時間経過とともに、ゾンビ数は次の式に従って増えていく。「元々いたゾンビに加え、そのゾンビらが噛み付いて新たに発生したゾンビが全ゾンビ数になる」という関係式だ。

すなわち、ゾンビ数 z(t) は公比が 1+r の等比数列で表されるので、ゾンビ数は次の式に従うことになる。この数のゾンビで街が埋め尽くされるのは地獄絵図だろうが、数式の見た目は非常に美しい。

1.2 ゾンビと戦う場合

　さて、増え続けるゾンビを前に、人類の存続を懸けゾンビと戦う場合を考えてみよう。時刻 t = S から攻撃（反撃）を開始するとし、単位時間あたりに退治できるゾンビ数を k と仮定する。このとき、ゾンビ数はどう表すことができるだろうか？

　まず、攻撃開始前のゾンビ数は先ほど考えた「逃げ続ける場合」と同じだということは分かるだろう。すなわち、ゾンビ数は次のように表すことができる（式に書いてある s.t. は "such that" の略で、「〜のとき」と訳しておこう）。

　一方、それ以降はゾンビを一定数撃退し続けるので、この式は成り立たない。k だけ撃破すると仮定しているので、ゾンビ数は次式のようになる。

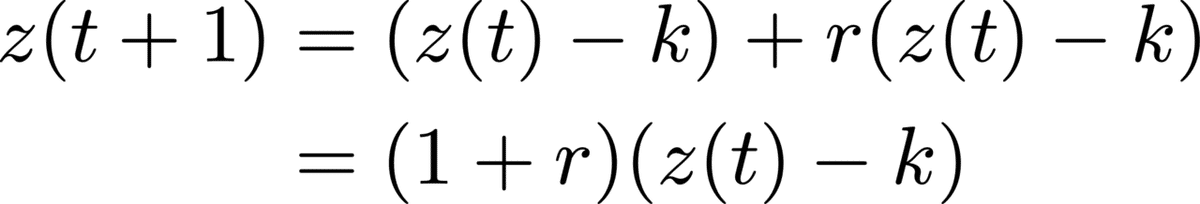
　いったん整理すると、次のようにまとめることができる。

　さて、いずれの場合も z(t) = ... の式で表したいので、攻撃開始以降の式を次のように変形してみよう。

これで等比数列の形で表すことができたので、z(t) が一般項として次のように求まる。

別の表し方

　これまではゾンビが r 人を新たにゾンビにする、という仮定の下で計算を進めてきたが、あえて r-1 人とするとどうなるだろうか？この場合、ゾンビ数は次のようにまとめることができると分かるだろう。

よって、

となり、少しだけすっきりした形で書くことができる。

2. 日常との対応

　ゾンビの数という非日常を考えたように思えるが、実は日常のシーンにも置き換えて考えることができる。例えばゾンビではなく、インフルエンザなどの感染症ウイルスだったらどうなるだろうか？今回は簡単な仮定の下で計算を行ったが、より精緻な仮定を置けば、十分現実の感染過程のシミュレートができるようになるだろう。

　実は感染症に関しては SIRモデル として数理モデルが考えられており、代表的なモデル式も存在する。"SIR" とは、それぞれ次の通りである。

- S: 感受性保持者（感染可能性のある人） (Susceptibles)
- I: 感染者 (Infected)
- R: 免疫保持者 / 隔離者 (Recovered/Removed)

　有名なモデルとしては ケルマック・マッケンドリックモデル があり、一番シンプルなものは次のような微分方程式で表される。

ここで、β は感染率、γ は隔離率を表す。この式における初期条件や値の条件等により、感染症が流行してしまうのか、自然に消滅するのかが計算できることになる。

おわりに

　本著では、ゾンビの数という非日常なシーンに対しての数式を考えたが、実は感染症モデルといった医療分野への応用も考えることができ、なかなか無下に扱うことはできないということが分かる。

　また、ゾンビ数を計算しておくことで、映画やドラマを観ている時も「今どれくらいゾンビがいるのか」がイメージできるようになり、より作品を楽しめることに繋がると期待している。

リンク

※ PDFのリンクはこちらです。（A5 / 10ページ）

※ 内容は以上が全てです。これ以降文章はありませんが、「投銭」として最後に購入ボタンを設定しています。気に入っていただけましたら応援宜しくお願いします。