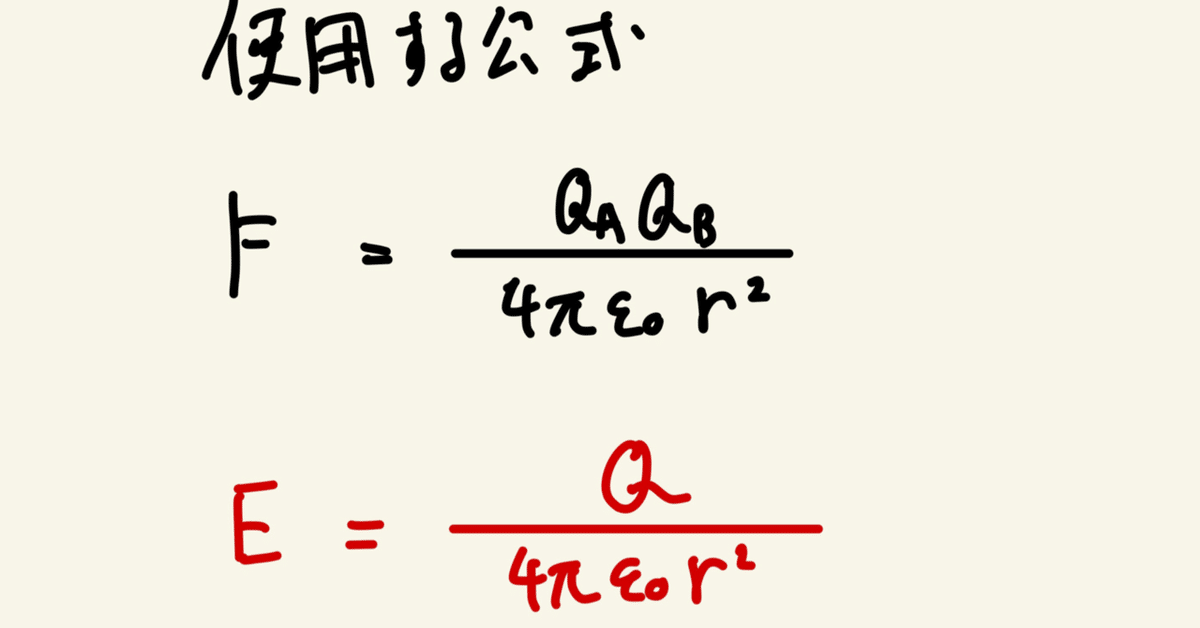
矢印を分解(電験二種理論H21問1)

並行して進めてる訳ではないが法規をどうするか頭を抱えている。

問1 電磁気の問題

わからないものは今回書かなかった。
勘で当てるものはいらない。
ちゃんと答えを導けるようにする。
では順序よくやっていく。

⑴について。
正電荷同士には反発力（斥力）が働くというのはまあ問題文にもあるし、わかると思う。
状況を図に書き込み、公式も書いてみる。

画像より正電荷に働く静電力は

となり、⑴の答えは(ホ)であることがわかる。

⑵について。
正電荷は点P2の電荷を吸引する、図に書き込むと

距離も使うので書いておいた、公式に代入すると

ここでのマイナスの斥力が働く、つまり引力なので画像のF1の矢印の向きに吸引力が働いている。
矢印をx成分とy成分へ分解する。

F1、F3は大きさは同じで向きが違うと考えてくれれば良い。
それぞれ分解するとy成分は同じ大きさで互いに反対方向、x成分は同じ大きさで同じ向きとなっている。
よって、y成分は打ち消しあい0となり、合力はx成分を足し合わせれば良い。
足し合わせたものが画像右下となる。
以上より、⑵の答えは(ヌ)となる。

⑶について。
点電荷が作る電界の公式

この式出てこなかったな・・・
これを参考に図へ情報を書き込む。

電界もx軸方向、y軸方向になるよう分解した。

y成分は同じ大きさで互いに逆向きなので0になることがわかる。
よって、⑶の答えは(ト)となる。

⑷について。
y成分は0なので3つの合成電界はx成分を足し合わせればよい。

計算すると画像右下となる、よって⑷の答えは(ハ)となる。

⑸について。
P2をPxへ移動した時合成電界が0になるところを探す。
つまり以下の二つの式が等しくなれば良い。

rの二次方程式を解いて

このrはグラフで言うと以下の場所である。

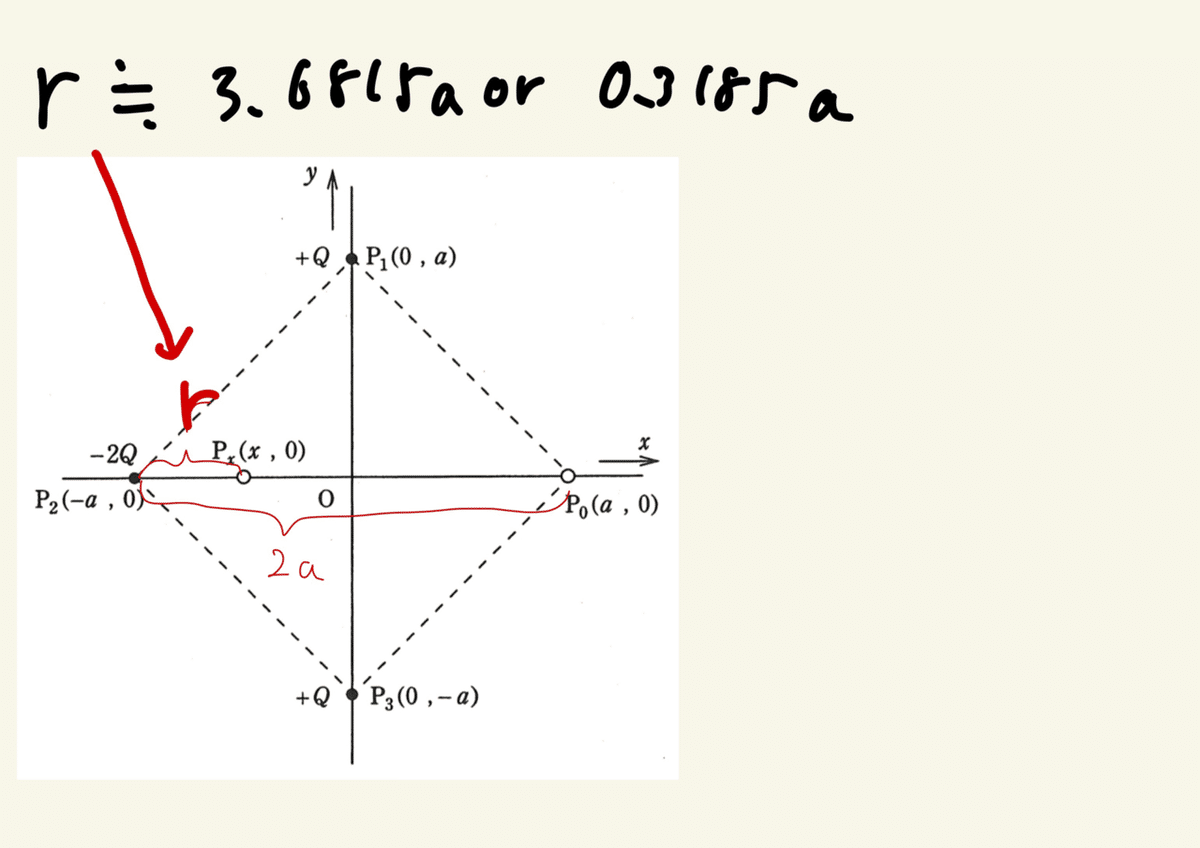
よって座標xは-aから右に0.3185a進んだ所となる。

以上より⑸の答えは(ニ)となる。

あとがき

一個式忘れると後半で躓いた。
解説は見てないので電界の式がわかった途端に
全部解けるっていうね。

微分とか使うのかと思ってしまったよ笑

ベクトルをsin、cosで分解できるようにしとくのは本当に重要。
それがわからなくて嫌になった時結構あったので…

午後も頑張るぞい、ではでは。