【灘中学校2020年度入試(1日目)第8, 10問】図形問題、本格化

今回も灘中学校2020年度入試第1日の算数を取り上げます。第8問と第10問です。

灘中学校・高等学校
2011年8月28日、Saoyagi2撮影、Wikipediaより

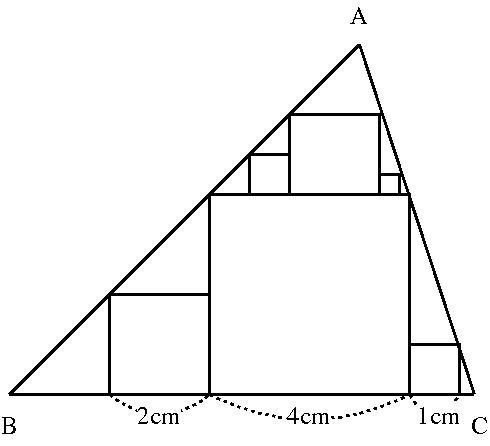
[問題8] 下の図(原文は右の図)のように三角形 ABC に 6個の正方形がぴったりと入っています。三角形 ABC の面積は (①　　　)cm2，6個の正方形の面積の和は (②　　　)cm2 です。

[問題終わり]

この問題も前回の問題7 と同じでひたすら平行線と相似を駆使(くし)します。

いきなり寸法を書くと上の図のようになります。

黄色い三角形GBE を見ると、ID // HE かつ ID = 2cm, HE = 4cm であるので、BD : BE = 1 : 2 になります。ということは、BD : DE = 1 : 1 であるので、BD = DE = 2cm となります。

同じように考えると、 三角形JFC に対して KG // JF かつ KG = 1cm, JF = 4cm であるので、CG : CF = 1 : 4 となり、CG : GF = 1 : 3 となります。よって、CG = GF ÷ 3 = 1/3 cm となります。

さらには、三角形 ALB と HEB、三角形 JFC と ALC は相似であり、AL : LB = HE : EB = 1 : 1 かつ AL : LC = JF : FC = 3 : 1 であるので、LB = AL かつ LC = AL ÷ 3 となります。

したがって、BC = LB + LC = AL + (AL ÷ 3) = AL × (4/3) = 9 + (1/3) = 28/3 から、AL = 7cm が得られます。以上より、① 三角形 ABC の面積 = (28/3) × 7 ÷ 2 = 98/3 = 32 + (2/3) cm2 となります。

正方形の面積の合計ですが、まず下の3つの正方形の面積の和は (2 × 2) + (4 × 4) + (1 × 1) = 21cm2 となります。また、三角形 AHJ は 三角形 ABC に相似で、高さを比較することで相似比は (7 - 4) : 7 = 3 : 7 となります。したがって、上の3つの正方形の面積の和は 21 × (3/7) × (3/7) = 27/7 = 3 + (6/7)cm2 となります。したがって、② 6つの正方形の面積の和 = 21 + 3 + (6/7) = 24 + (6/7)cm2 となります。

[問題10] 下の図(原文では右の図)のような台形ABCD がありまる。この板を辺CD の周りに 1回転させたとき，この板の通過する部分の体積は(　　　)cm3 です。

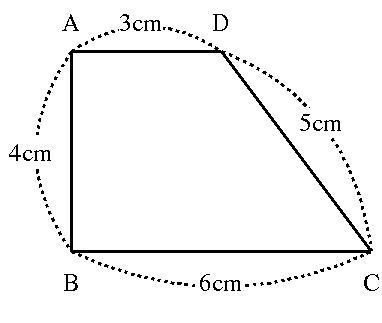
ただし，円周率は 3+(1/7) とします。また，板の厚さは考えません。

[問題終わり]

辺 AB で回転させる問題ならば簡単ですが、さすがは灘中学校です。単純にはいきません。とはいえ、これも相似を駆使(くし)するだけです。

辺CD の周りで回転するので、細かく刻んで求めるしかなさそうです。ということで、上の図のように線を入れてみました。

D から BC に垂直な線を引いたときの BC 上の点を H とすると、三角形 DHC はいわゆる 3 : 4 : 5 の三角形です。これに相似な三角形が多数できるので覚えておいてください。

必要となるのは、辺BG, CG, EG, EF, FD, AF の長さとなるでしょうか。そのうちのいくつかは必要なくなるかもしれませんが。

まずは辺 BG と CG の長さを求めてみましょう。

三角形 BCG は BC : CG : BG = 5 : 3 : 4 であるので、BG = (4/5) × BC = (24/5)cm 、CG = (3/5) × BC = (18/5)cm が得られます。

次に三角形 EBC を見てみます。これは三角形 DHC の2倍になっているので、辺 EB = 8cm, EC = 10cm となります。したがって、EA = 4cm, ED = 5cm となります。

多分、これだけあれば十分だと思います。

まず、三角形 EBC を EC の周りに1回転してできる図形の体積を求めます。

これは三角形 EBG と CBG の 2つに分けて考えるのが基本ですが、どちらも底面積は半径を BG とする円の面積であるので、それに(高さの合計)＝(辺 EC の長さ) を書けて 1/3 倍すればいいので、まとめて求めることができます。

計算すると、

BG × BG × (22/7) × EC × (1/3) = (24/5) × (24/5) × (22/7) × 10 × (1/3)

が得られます。具体的に計算するのは後回しにします。

次に、三角形 EAD をED の周りに1回転してできる図形の体積を求めますが、実は先ほどの三角形 EBC のときと図形に対する相似比 1/2 の相似図形になるので、体積は 1/8 となります。

よって、最終的に求める体積は

(24/5) × (24/5) × (22/7) × 10 × (1/3) × (7/8) = 1056/5 = 211+(1/5)cm3

となります。

見ての通り、この段階になってようやく約分が発生して式がきれいになります。ですので、先ほどの段階で計算するのは得策ではありません。しかも、円周率を 3.14 ではなく 22/7 としているために計算がすごく楽になっています。(最後の式で 7 が約分されている！)

さて、今回の2問ですが、問題8 も問題10 もどのように計算するかで運命の分かれ道になると思います。

例えば問題8 の場合は、すべての正方形について 1辺の長さを求めると大変なことになります。ここでは上の3つの正方形の面積の和が(簡単に求められる)下の 3つの正方形の面積の合計の (3/7)×(3/7)倍ということを使って簡単に求めています。

問題10 にしても、辺 EF, FD, DG の長さを求めようとすると時間がかかってしまいます。それは避けたい。

今回、どちらも解きながらこの note を書いていましたが、問題10 では最初、辺 EF, FD, DG の長さを求める方向で考えてはいたものの、まとめて体積が求められる部分を意識しながら解いていたら、今回の解答のようにずいぶんと簡単になりました。(実は CG の長さが無駄になっている！笑)

問題10 は空間図形の問題とは言え、基本的には平面図形の処理なので、紙に描きやすいし、いろいろと工夫できる問題になっていると思います。普段の鍛(きた)え方で解くのが速くなるはずです。という意味で、実力が解く速さになって返ってくる、いい問題ではないかと思います。

また今回飛ばした第9問についてはこちらをご覧ください。

この第9問は平面図形の最後の問題になりますが、平面図形のボス的な存在です。気がつけば簡単だけど、気がつかなければ時間を食いかねない。私はこの問題と相性が良かったですが、合格者の中でもできなかった方がいらっしゃったかもしれません。難しい問題だと思います。

第9問と第11問はともかく、灘中学校の受験生であれば他はできれば取りたい。おそらくこの辺りの問題で合格者と不合格者を分けているのではないかという印象を受けました。