線型代数、ベクトル、行列、その理解の意義について。~行列編~

さて、ちょっと前回記事からちょっと日が開いてしまいました。。。仕事で立場が変わり少しドタバタしていたことと、gaccoの統計学Ⅲの習得に追われていた。。。ということにしておきます。（満点、取れませんでした。。。悔しい。。。）

さて、前回記事では、なぜ機械学習でベクトルの扱いが中心的な命題になるのか、について軽く触れました。今回は、なぜベクトル演算とセットで行列の扱いが出てくるのか、について。

最初に結論を一言でいうと、「行列がベクトルに対して唯一線型変換を与えるものになるから」です（線型変換については、以前の記事で少しだけ触れていますので、ご参照あれ。。。ところで、最近、線型じゃない関係性ってなんなのか、いまいちよく分からなくなってきたので、ちょっとこの本読んできます。このシリーズ、厳密さという観点ではまだあまり深く読み込んでいないためにちょっと判断できないのですが、ツールとして扱うために各分野にある理論の概要を知るにはとても良いシリーズですね）。

ベクトルの内積（スカラー積）

さて、行列とベクトル、あるいは行列同士の演算を語るにあたり、最初にベクトルの内積について語ります。次元の同じ2つのベクトルは、同じ要素同士の積の和を内積として定義できます。つまり、​v1 = (x1, x2, ...),  v2 = (y1, y2, ...) として、v1 * v2 = Σ(xiyi) というスカラー量を定義できます。また、ベクトルには縦方向に要素を並べた列ベクトルと、横方向に要素を並べた行ベクトルを定義することがありますが、同じ次元の行ベクトル*列ベクトルの積を内積とすることが出来ます（ちなみに、列ベクトル*行ベクトルの積はスカラーになりませんし、次元数が異なっても積が成立します）。また、幾何ベクトルとして考えた場合、上記内積の値は、ベクトル同士の為す角をθとすると、|v1||v2|cosθという値になります。θに着目すると、この値は「ベクトル同士の向く方向が似ているほど大きな値をとりやすく、一致しているときで最大、正反対方向で最小の値をとる」ような値となります。

ちなみに、ある互いに独立な変数x1 ~ xnの線型結合ΣCi*Xiについても、ベクトルの内積として表現できたりします。つまり、

（C1 C2 ... Cn）* (X1 X2 ... Xn)T

※Tは転置を示す。この場合は行ベクトル（X1 X2 ... Xn）を列ベクトルに直したものとする演算

みたいな形になるわけです。

行列の積

さて、行列の積についてですが、まず行列を「列ベクトル、行ベクトルの束」としてとらえてみます。すると、以下の図のように書けるのではないかと。

行ベクトル

列ベクトル

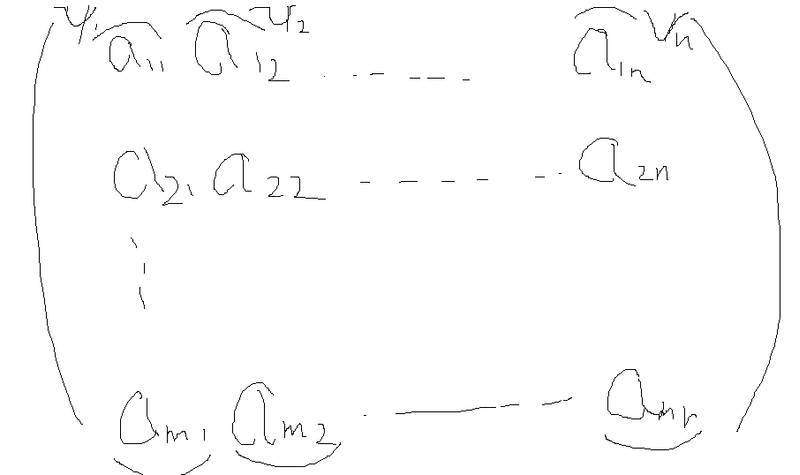
そんで、これらのベクトルをそれぞれh1, h2, ..., hn、およびv1, v2, ...,vnと定義してみると、h1 ~ hn、v1 ~ vnの間に、n×n通りの内積が定義できるワケです。そこで、aij = hi*vjとして（aijはスカラー量）、新しい行列を構成するワケです。これが行列積になります。当たり前ですが、内積は要素数が同じ場合にのみ定義できますので、行列積が定義可能な条件として、上記で構成される行ベクトルと列ベクトルの要素数が同じになる必要があります。すなわち、行列積は「左側行列の列数と右側行列の行数が一致する場合にのみ定義可能」なワケです（正方行列である場合は、こんなもの考える必要が無いので扱いがラクですね）。そんでもって、行列積の型は、左側行列がn行p列型、右側行列がp列m行型である場合は、n行m列型の行列になります。

さて、スカラー積（いわゆる掛け算）では、右側の数字と左側の数字を交換しても演算結果が変わらない、「交換法則」が成立していました。が、上記定義からわかるように、行列の場合にいは左側行列と右側行列を交換した場合は定義できないこともあり、交換法則は成立しません。これは行数と列数が一致している正方行列においても同じく一般には成立しません。

さて、上記のmやらnやらpやらには、無限ではない任意の自然数が入ります。当然1も入ります。行列というのは、行ベクトルや列ベクトルが束になって構成されていますが、mやらnやらpやらが1になると、行列は単独の行ベクトル、あるいは列ベクトルとなります。そして、1行p列の行ベクトル×p行1列の列ベクトルについては、1行1列の行列（つまりスカラー）として行列の積が定義可能です。一方、p行1列の列ベクトルと1行q列の行ベクトルでは、演算結果はp行q列の行列になります。

行列とベクトルの積

さて、行列、およびベクトルの積について一通り定義したところで、あるn次正方行列Aと、n次列ベクトルxに対して、行列Aを左からかけてみます。すると、Aを構成するn個のn次元行ベクトルaiと列ベクトルxの内積（つまり線型結合）の集合にて、あたらしいn次ベクトルyを作ることができます。すなわち、

Ax = y

なる形で、n次正方行列Aはxベクトルを新しいベクトルyへと変換したことになります。ここで、行列Aによる列ベクトルxの変換は、線型性を満たすことになります。逆に、xベクトルに対して左から積をとることでyベクトルに変換するような行列は一意に決めることができます。また、任意のn次元列ベクトルからn次元列ベクトルへの線型写像はn次の行列の積以外に存在しません。また、仮にyがm次列ベクトルである場合も行列の型をm行n列型の行列としておけば変換することが出来ます。

先の記事で、ベクトルは対象の状態を表現するのに良いから機械学習をはじめとしたあらゆる分野でモデルの数式的な表現の際に扱うのだとしました。一方、線型変換は私たちの身の回りにあるごくありふれた、それでいて人間にとって扱いやすい写像であり、そしてn次列ベクトルに対する線形写像は左側からの行列の積で与えられます。つまり、繰り返しになりますが、ベクトルと行列による演算は、ある状態から別の状態への線型的な操作、ないしは遷移を表現するのに大変便利なツールであるということです。例えば、ある瞬間に観測可能な要素がn個ある系の時系列変化について、ある測定aと測定bの間の関係が線型性を持つと仮定すると、ベクトルと正方行列Aの積によって表現したくなるワケです。図にするとこんな感じ（ｸｿﾍﾀお絵描きおじさんゆえ見づらいのはご容赦いただきたい）